
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Для випадку з відомим СКВ генеральних сукупностей
|
|
Відомі σx і σy величин X і Y. Висуваємо гіпотезу H0: vх=vy при альтернативній H1: vх ≠ vy. Необхідно визначити, чи істотна розбіжність між середніми  і
і  , отриманими відповідно з вибірки обсягом п1 для випадкової величини Хі обсягом п2 для випадкової величини Y.
, отриманими відповідно з вибірки обсягом п1 для випадкової величини Хі обсягом п2 для випадкової величини Y.
Позначимо
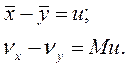
Розглянемо різницю и як параметр Z, тобто у вигляді нормованої різниці
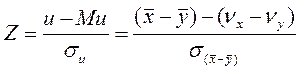
де 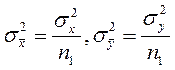 а при висунутій гіпотезі
а при висунутій гіпотезі 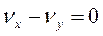
Величини Хі Y — незалежні величини, для яких 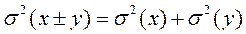 тому можна записати
тому можна записати
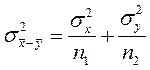 (2.7)
(2.7)
Для перевірки правильності гіпотези використовують двобічну критичну область. З урахуванням виразу (16.1) значення статистичної характеристики
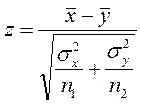
Значення z порівнюють із критичним значенням 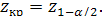 Якщо
Якщо 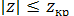 приймають гіпотезу Н0.
приймають гіпотезу Н0.
Для випадку з невідомими СКВ генеральних сукупностей. У цьому разі визначають емпіричне значення s і використовують статистичну характеристику
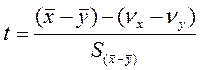
розподілену за законом Стьюдента.
Відомо, що для незалежних випадкових величин
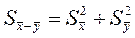
За умови, що вибірки взято з однієї генеральної сукупності, тобто 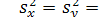 можна записати
можна записати
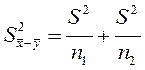
або
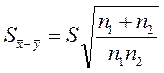 (2.8)
(2.8)
Зважаючи на те, що вибірки взято з однієї генеральної сукупності, доцільно скористатися всіма наявними експериментальними даними, тобто розглядати вибірку обсягом п1 + п2. Це дає змогу підвищити статистичну надійність знайденої оцінки СКВ генеральної сукупності. Тоді
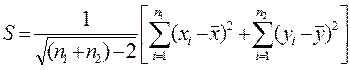 (2.9)
(2.9)
Виходячи з виразу для дисперсії, можна записати:
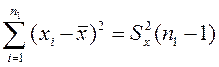
Аналогічно маємо:
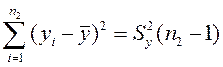
Підставляють отримані значення сум у вираз (2.9) і дістають:
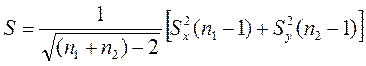 (2.10)
(2.10)
Підставляють вираз (2.10) у вираз (2.8) і отримують
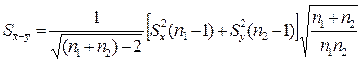 (2.11)
(2.11)
З урахуванням виразу (2.11) розрахункове значення коефіцієнта Стьюдента буде
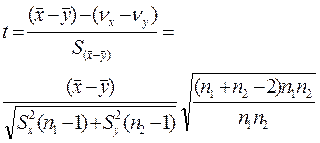
Для перевірки гіпотези необхідно знайти критичне значення коефіцієнта Стьюдента tкр Для заданого рівня статистичної значущості α і кількості ступенів свободи п1 + п2.- 2. Якщо розрахункове значення |tр| ≤ tкр, приймають нульову гіпотезу.
У випадку, коли вибірки взято не з однієї генеральної сукупності, тобто 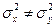 для визначення суттєвості розбіжності обчислених середніх
для визначення суттєвості розбіжності обчислених середніх  і
і  коефіцієнт Стьюдента обчислюють за формулою:
коефіцієнт Стьюдента обчислюють за формулою:
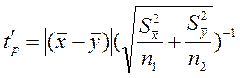
Обчислене значення 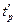 порівнюють із критичним значенням коефіцієнта Стьюдента, яке залежно від α і кількості ступенів свободи обчислюють за формулою
порівнюють із критичним значенням коефіцієнта Стьюдента, яке залежно від α і кількості ступенів свободи обчислюють за формулою
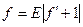
де
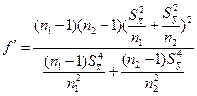
Порівняння двох дисперсій. Другою важливою ознакою, за якою можуть порівнюватися дві сукупності, є дисперсії в кожній із них. Гіпотези про дисперсії відіграють важливу роль у техніці, оскільки саме дисперсія характеризує такі важливі конструкторські й технологічні показники, як точність приладу, похибку результату, точність технологічного процесу тощо.
При спільній обробці результатів необхідно, насамперед, переконатися в тому, що умови проведення дослідів, при яких отримані результати, були однаковими. З цією метою можна використати оцінку розбіжності дисперсій.
F-критерій (розподіл Фішера). Припустимо, що задано дві генеральні сукупності X та Y з нормальним розподілом X 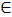 N (µ1, σ1) і Y
N (µ1, σ1) і Y 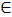 N (µ2, σ2). Із цих генеральних сукупностей зроблено незалежні вибірки з параметрами відповідно п1,
N (µ2, σ2). Із цих генеральних сукупностей зроблено незалежні вибірки з параметрами відповідно п1, 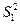 , п2,
, п2, 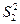 . Потрібно при рівні значущості α перевірити гіпотезу
. Потрібно при рівні значущості α перевірити гіпотезу 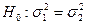 при альтернативній гіпотезі.
при альтернативній гіпотезі. 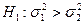
Математик-статистик Р. Фішер установив, що відношення незсунених оцінок двох дисперсій підпорядковується закономірності, що залежить від кількості ступенів свободи цих дисперсій. Припускаючи, що 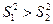 , приймають як статистику величину F, котра задовольняє F-розподіл, для якого
, приймають як статистику величину F, котра задовольняє F-розподіл, для якого 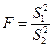 з кількістю ступенів свободи, що дорівнює п1 – 1 і п2 – 1 відповідно.
з кількістю ступенів свободи, що дорівнює п1 – 1 і п2 – 1 відповідно.
Критична область буде тільки правобічна і визначається умовою. 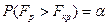
Значення 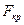 знаходять із таблиць F-розподілу, яке залежить від трьох величин: рівня значущості α і двох чисел, якими виражаються ступені свободи
знаходять із таблиць F-розподілу, яке залежить від трьох величин: рівня значущості α і двох чисел, якими виражаються ступені свободи 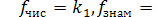 . Таблиці складені окремо для кожного значення α (тривимірні таблиці). Задаючись рівнем статистичної значущості α, вибравши в таблиці колонку
. Таблиці складені окремо для кожного значення α (тривимірні таблиці). Задаючись рівнем статистичної значущості α, вибравши в таблиці колонку 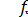 і рядок
і рядок 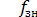 , на їх перетині знаходять критичне значення коефіцієнта
, на їх перетині знаходять критичне значення коефіцієнта 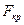 .
.
Якщо 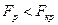 можна стверджувати на підставі наявних експериментальних даних, що при рівні статистичної значущості а вибіркові дисперсії будуть однорідні.
можна стверджувати на підставі наявних експериментальних даних, що при рівні статистичної значущості а вибіркові дисперсії будуть однорідні.
Іноді перед обробкою даних необхідно переконатися в однорідності дисперсій, отриманих на підставі даних двох експериментальних вибірок. У цьому випадку також використовується критерій Фішера.
Відмінністю є те, що альтернативна гіпотеза 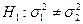 . Для перевірки гіпотези використовують двобічну критичну область (рис. 2.8), тобто передбачається, що ймовірність того, що розрахункове значення
. Для перевірки гіпотези використовують двобічну критичну область (рис. 2.8), тобто передбачається, що ймовірність того, що розрахункове значення 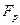 буде меншим за критичне значення
буде меншим за критичне значення 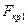 або більшим за
або більшим за 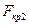 не перевищує значення
не перевищує значення
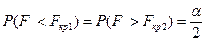
Оскільки в таблиці є тільки значення 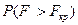 , то значення
, то значення 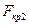 можна знайти безпосередньо з таблиць.
можна знайти безпосередньо з таблиць.
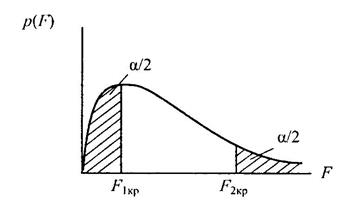
Рис. 2.8
Для визначення 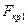 , яке відповідає умові
, яке відповідає умові 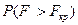 , вводять коефіцієнт
, вводять коефіцієнт
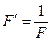
Тоді
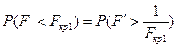
Останнє співвідношення показує, що 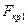 можна знайти виходячи з умови
можна знайти виходячи з умови 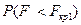 . Надалі перевірка залишається такою самою, як і для однобічної критичної області, тобто нуль-гіпотеза, приймається в тому випадку, коли розрахункові значення
. Надалі перевірка залишається такою самою, як і для однобічної критичної області, тобто нуль-гіпотеза, приймається в тому випадку, коли розрахункові значення 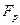 містяться між критичними
містяться між критичними 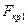 й
й 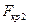 .
.
Перевірка гіпотези про однорідність ряду дисперсій. (G- критерій). Якщо потрібно побудувати аналітичну залежність (аналітичну модель) на основі експериментальних даних, то насамперед необхідно переконатися в однорідності вибіркових дисперсій. Для цього серед наявних вибіркових дисперсій вибирають максимальну, а потім розглядають відношення максимальної дисперсії до суми всіх вибіркових дисперсій. Для випадку, коли обсяги вибірок однакові, тобто в кожній вибірці дисперсія обчислювалася на підставі однакової кількості даних m, застосовують G-критерій (критерій Кохрена). Статистика G вказує, яку частку має максимальна дисперсія в загальній дисперсії, і обчислюється за формулою:
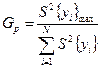
де 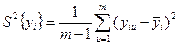 — дисперсія для кожної i-ї вибірки, і=1,
— дисперсія для кожної i-ї вибірки, і=1, 
Висувають гіпотезу Н0: дисперсії однорідні. Для перевірки нульової гіпотези знайдене розрахункове значення Gр порівнюють із критичним значенням коефіцієнта Gкр, яке знаходять із таблиць критичних значень G-критерію на перетині стовпця 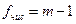 та рядка
та рядка 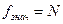 для заданого рівня статистичної значущості α.
для заданого рівня статистичної значущості α.
Якщо 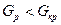 на підставі наявних даних можна стверджувати, що вибіркові дисперсії будуть однорідні, тобто гіпотеза Н0 приймається.
на підставі наявних даних можна стверджувати, що вибіркові дисперсії будуть однорідні, тобто гіпотеза Н0 приймається.
Якщо гіпотеза про рівність дисперсій відхиляється, то збільшують обсяг вибірок і знову перевіряють гіпотезу. Якщо ж гіпотеза знову не підтверджується, такі вибіркові дані спільно обробляти не можна
Питання для самоперевірки
1. Що називається параметричним критерієм?
2. Записати критерій перевірки гіпотези про рівність двох середніх із відомим СКВ.
3. Записати критерій перевірки гіпотези про рівність двох середніх з невідомим СКВ.
4. За яким критерієм перевіряють гіпотези про рівність дисперсій двох вибірок?
5. Як перевіряють гіпотези про рівність дисперсій двох вибірок при правобічній критичній області?
6. Як перевіряють гіпотези про рівність дисперсій двох вибірок при двобічній критичній області?
7. За яким критерієм та як перевіряють гіпотези про рівність дисперсій кількох вибірок?
8. Як користуватися таблицями F-розподілу та G-розподілу?
2.4 Критерії згоди
Критерії згоди використовують для перевірки узгодженості наявних експериментальних даних з теоретичним законом, що припускається.
Розглянуті раніше методи перевірки гіпотез припускали, що функціональна форма закону розподілу відома, й визначалися лише значення параметрів цього закону.
Однак у деяких випадках сам вид закону розподілу потребує статистичної перевірки. Раніше було розглянуто, як, зіставляючи ймовірності потрапляння значень в інтервали з відповідними частостями, отриманими зі спостережень, або проводячи графічне порівняння полігонів і гістограм із кривою розподілу, можна скласти первинне уявлення про близькість теоретичного та емпіричного розподілів.
Постає питання про критерії перевірки гіпотези про те, що величина X відповідає конкретному закону розподілу зі щільністю ймовірності р(х).
Подібні критерії зазвичай називають критеріями згоди (відповідності). Вони грунтуються на виборі певної міри розбіжності між теоретичним та емпіричним розподілами. Якщо така міра розбіжності для розглянутого випадку перевищує встановлену межу, гіпотеза відхиляється й навпаки.
Таким чином, перевірити таку гіпотезу — означає переконатися в тому, що наявні дані справді взято з генеральної сукупності, яка має передбачуваний закон розподілу.
Розглянемо застосування одного з найбільш уживаних критеріїв χ2-критерію Пірсона.
Критерій χ2 припускає, що наявні експериментальні дані розбивають на l елементарних інтервалів, кожний з яких містить не менш ніж 8—10 значень. За відомим правилом будують гістограму, за видом якої, якщо немає додаткових джерел, можна зробити припущення про можливий закон розподілу. Підбирають закон розподілу, якому щонайбільше відповідають наявні дані.
Для кожного елементарного інтервалу можна визначити  , — кількість значень, що потрапили в і- й інтервал, l = 1,...,l.
, — кількість значень, що потрапили в і- й інтервал, l = 1,...,l.
Висувають гіпотезу Н0: емпіричний розподіл належить до передбачуваного теоретичного. Для того щоб перевірити висунуту гіпотезу, необхідно оцінити розбіжності між емпіричною  , і теоретичною тi кількістю потраплянь за елементарний інтервал за припущення, що випадкова величина X має передбачуваний закон розподілу.
, і теоретичною тi кількістю потраплянь за елементарний інтервал за припущення, що випадкова величина X має передбачуваний закон розподілу.
Установлено, що величина
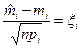 (2.12)
(2.12)
розподілена нормально з нульовим математичним сподіванням і одиничною дисперсією. Відомо, що сума квадратів нормованих нормально розподілених величин підпорядковується χ2-розподілу Пірсона:
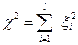
Виходячи з виразу (2.12) можна обчислити розрахункове значення χ2
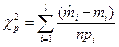 (2.13)
(2.13)
Вираз (2.13) використовують як статистику для перевірки гіпотези про передбачуваний закон розподілу.
Для знаходження теоретичної кількості потраплянь ті розглянемо співвідношення 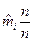 і запишемо його як
і запишемо його як 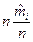 .
.
Відношення 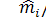 є частотою (частістю) потрапляння результатів у i -й елементарний інтервал. Відомо, що при збільшенні загальної кількості спостережень п частота наближається до теоретичної ймовірності pі потрапляння випадкової величини в і-й елементарний інтервал при передбачуваному законі розподілу. Виходячи із цього, можна записати:
є частотою (частістю) потрапляння результатів у i -й елементарний інтервал. Відомо, що при збільшенні загальної кількості спостережень п частота наближається до теоретичної ймовірності pі потрапляння випадкової величини в і-й елементарний інтервал при передбачуваному законі розподілу. Виходячи із цього, можна записати:
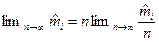
Пам'ятаючи про те, що границею, до якої прямуватиме  при збільшенні п, є теоретичне значення ті кількості потраплянь в інтервал, можна записати ті = прі.
при збільшенні п, є теоретичне значення ті кількості потраплянь в інтервал, можна записати ті = прі.
Таким чином, можна обчислити теоретичні значення ті, а потім знайти різницю  —ті, що характеризує розбіжність кількості потраплянь у кожний і- й інтервал.
—ті, що характеризує розбіжність кількості потраплянь у кожний і- й інтервал.
Потрапляння результатів в і- й інтервал характеризується біноміальним законом розподілу, для якого
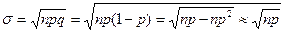
Для знаходження рі, необхідно користуватися співвідношенням
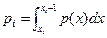
де хі й хі+1 — кінці інтервалу, а р(х) наприклад, для нормального закону має вигляд:
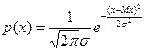
У випадку, коли Мх і σ невідомі, необхідно обчислити їхні оцінки  і s на підставі дослідних даних і увести їх у вираз для закону розподілу. Так, для нормального закону оцінка щільності ймовірності
і s на підставі дослідних даних і увести їх у вираз для закону розподілу. Так, для нормального закону оцінка щільності ймовірності
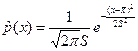
Оскільки на підставі тих самих експериментальних даних додатково обчислюють  і s то втрачаються два ступені свободи, тобто f=l-1-2.
і s то втрачаються два ступені свободи, тобто f=l-1-2.
Отримане значення 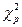 порівнюють із критичним
порівнюють із критичним 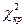 , узятим з таблиці χ2 — розподілу для обраного рівня статистичної значущості α і кількості ступенів свободи f=l-3.
, узятим з таблиці χ2 — розподілу для обраного рівня статистичної значущості α і кількості ступенів свободи f=l-3.
Якщо 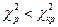 можна стверджувати, що з обраним рівнем статистичної значущості α приймається гіпотеза Н0, тобто наявні дані відповідають передбачуваному закону розподілу. Гіпотеза Н0 відхиляється при значеннях
можна стверджувати, що з обраним рівнем статистичної значущості α приймається гіпотеза Н0, тобто наявні дані відповідають передбачуваному закону розподілу. Гіпотеза Н0 відхиляється при значеннях 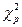 , більших за
, більших за 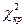 тому використовується тільки правобічна критична область (див. рис. 2.7, б).
тому використовується тільки правобічна критична область (див. рис. 2.7, б).
Взагалі у практиці перевірки гіпотез про відповідність закону розподілу намагаються застосовувати два методи перевірки, що підвищує вірогідність прийняття рішення. Особливо це важливо, коли характерні риси закону розподілу перебувають на його «хвостах», що не завжди можна виявити при малому обсязі випробувань.
Критерій ω2 (омега-квадрат). Критерій χ2, незважаючи на свою простоту, не завжди забезпечує надійну перевірку гіпотези про закон розподілу, оскільки частина вихідної інформації втрачається при здійсненні процедури групування даних.
Розглянемо критерій згоди при простій гіпотезі, що повністю фіксує закон розподілу генеральної сукупності, з якої отримано вибірку. Цей критерій, що дістав назву ω2, на відміну від χ2 грунтується безпосередньо на спостережених (незгрупованих) значеннях величини X.
Нехай гіпотеза полягає в припущенні, що величина X розподілена відповідно до деякого неперервного закону розподілу з інтегральною функцією F(x), яка вважається відомою.
Розглянемо ряд вибіркових значень х1,х2,...,хп випадкової величини X. Позначимо пх – кількість значень, що перебуває ліворуч від вибраного значення. Тоді відношення 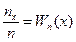 і є емпіричною функцією розподілу. При великому обсязі вибірки емпірична функція розподілу Wn(х) є апроксимацією теоретичної функції розподілу F(x).
і є емпіричною функцією розподілу. При великому обсязі вибірки емпірична функція розподілу Wn(х) є апроксимацією теоретичної функції розподілу F(x).
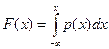
Різниця величин Wn(x) і F(x) може бути використана як міра розбіжності між вибірковими даними та передбачуваним законом розподілу генеральної сукупності. За міру цієї розбіжності беруть середній квадрат відхилень за всіма можливими значеннями аргументу:
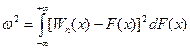
де 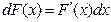
З наявних вибіркових даних будується варіаційний ряд 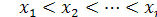 Теоретично рівність будь-яких двох членів у цьому ряді через неперервність функції F(х) практично неможлива, тобто має ймовірність, що дорівнює нулю. Вважаємо, що для х<x1 емпірична функція розподілу дорівнює нулю, а при х>хп, дорівнює одиниці. Відповідно до такого визначення функції Wn(x) маємо:
Теоретично рівність будь-яких двох членів у цьому ряді через неперервність функції F(х) практично неможлива, тобто має ймовірність, що дорівнює нулю. Вважаємо, що для х<x1 емпірична функція розподілу дорівнює нулю, а при х>хп, дорівнює одиниці. Відповідно до такого визначення функції Wn(x) маємо:
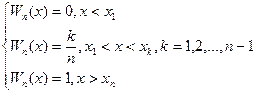 (2.14)
(2.14)
Емпірична функція стрибком змінює свої значення в точках x=xk на 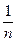 , зберігаючи це значення протягом усього інтервалу xk – xk+1 (рис. 2.9)
, зберігаючи це значення протягом усього інтервалу xk – xk+1 (рис. 2.9)
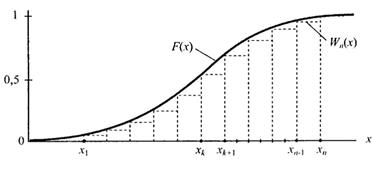
Рис. 2.9
Виходячи зі співвідношення (2.14), можна подати вираз для критерію ω2 у вигляді окремих доданків:
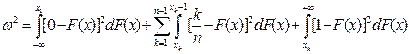
(2.15)
Розглянемо першу складову інтеграла (2.15):
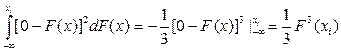 (2.16)
(2.16)
Розглянемо другу складову інтеграла (2.15)
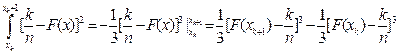 (2.17)
(2.17)
Розглянемо третю складову інтеграла (2.15):
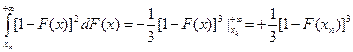 (2.18)
(2.18)
Підставляючи доданки (2.16), (2.17), (2.18) у вираз (2.15), дістаємо:
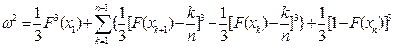
Після спрощень останній вираз набирає вигляду:
 (2.19)
(2.19)
Ця рівність показує, в який спосіб ω2 залежить від індивідуальних членів варіаційного ряду.
Точний розподіл ω2 дуже складний, але дослідження показують, що вже при n > 40 розподіл добутку nω2 близький до деякого граничного розподілу, для якого складено таблиці. Фрагмент такої таблиці наведено далі:
| α | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| (nω2)кр | 0.1184 | 0.1467 | 0.1843 | 0.2412 | 0.3473 |
| α | 0.05 | 0.03 | 0.02 | 0.01 | 0.001 |
| (nω2)кр | 0.4614 | 0.5489 | 0.6198 | 0.7435 | 1.6979 |
За таблицями визначають критичні значення для величини nω2 при n > 40:
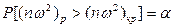
Якщо розрахункове значення критерію буде меншим від критичного, приймають гіпотезу про передбачуваний закон розподілу.
Питання для самоперевірки
1. Які критерії називаються критеріями згоди?
2. Як за критерієм χ2 перевіряють гіпотезу про закон розподілу?
3. Яка міра розбіжності між емпіричним та теоретичним розподілом застосовується для критерію χ2?
4. Яка величина підлягає розподілу χ2?
5. Як визначається кількість ступенів свободи для розподілу χ2?
6. Яка величина застосовується як статистика для перевірки гіпотези про закони розподілу?
7. Чому використовується тільки правобічна критична область?
8. Які характерні особливості має критерій ω2?
9. Яка міра розбіжності між емпіричним та теоретичним розподілом застосовується для критерію ω2?
10. Як знаходиться критичне значення для критерію ω2?
2.5 Непараметричні критерії
У непараметричних критеріях не робиться припущень щодо розподілу генеральної сукупності. Вони застосовуються при будь-яких законах як для кількісних, так і якісних ознак.
В експериментальних дослідженнях часто потрібно порівняти два паралельні ряди спостережень над об'єктами, що належать до різних різновидів, типів, сортів.
При цьому виконують N дослідів при систематичній і планомірній зміні від досліду до досліду рівня якого-небудь фактора, розбіжність у дії якого на кожний із двох різновидів об'єктів мають з'ясувати. У кожному такому досліді над парою об'єктів, виконаному, природно, у незмінних умовах, мають два значення порівнюваної ознаки двох об'єктів.
Непараметричні критерії використовуються для перевірки того, чи належать дві вибірки до тієї самої генеральної сукупності, тобто чи однорідні ці вибірки (значення результатів випробувань мають однакові функції розподілів). Такі критерії грунтуються на вивченні послідовностей реалізацій випадкової величини. Відповідні обчислювальні процедури є ефективними навіть при обмежених обсягах вибірок.
Критерій Уїлкоксона (критерійсерій). Цей критерій дає змогу на основі наявних вибірок, використовуючи інтегральну функцію ймовірностей, перевірити гіпотезу про те, що дві вибірки мають однаковий закон розподілу.
Таким чином, гіпотеза Н0: FX (х)=FY(х) перевіряється за допомогою однієї вибірки (x1,..., хп1) з Х і однієї вибірки (у1,...,уп2) із Y. Щодо розподілів X і Y ніяких припущень не робиться.
Значення x1,..., хп1 та у1,...,уп2 oбох вибірок упорядковуються у спільний варіаційний ряд. Коли в цьому ряді елемент однієї вибірки більший від елемента іншої вибірки, говорять, що пари значень (хi, yj) утворюють інверсію.
Під інверсією розуміють перехід від елемента однієї вибірки до елемента іншої вибірки при послідовному просуванні вздовж варіаційного ряду, причому інверсія не передбачається для першого елемента варіаційного ряду. Як контрольна величина береться повна кількість інверсій и.
Приклад. Для ряду 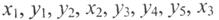 перед у1 є тільки один елемент х, а отже, кількість інверсій дорівнює одиниці. Елементу у2 передує один елемент х, кількість інверсій також дорівнює одиниці. Елементу у3 передують два елементи першої групи, а отже, кількість інверсій дорівнює двом. Аналогічно для у4 і у5. Повна кількість інверсій и= 1+1+2+2+2 = 8.
перед у1 є тільки один елемент х, а отже, кількість інверсій дорівнює одиниці. Елементу у2 передує один елемент х, кількість інверсій також дорівнює одиниці. Елементу у3 передують два елементи першої групи, а отже, кількість інверсій дорівнює двом. Аналогічно для у4 і у5. Повна кількість інверсій и= 1+1+2+2+2 = 8.
Для перевірки нульової гіпотези можна застосовувати два способи.
1. Якщо гіпотеза правильна, обчислене значення и не повинне відхилятися від свого математичного сподівання:
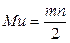 (2.20)
(2.20)
де m і n – обсяги вибірок.
Від гіпотези відмовляються, якщо 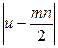 більше від певного критичного значення иα. Критичне значення иα беруть для заданого рівня значущості α з таблиці критичних значень Уїлкоксона.
більше від певного критичного значення иα. Критичне значення иα беруть для заданого рівня значущості α з таблиці критичних значень Уїлкоксона.
2. У загальному випадку, а також у випадку великих m і п, для яких иα,не можна взяти з таблиці, справджується формула:
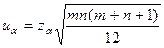
де z α — визначається з таблиць Лапласа.
Критерій знаків (медіанний критерій). Його використовують тільки в разі, коли вибірки Х та Y однакові за обсягом, тобто значення можна розглядати у вигляді масиву пар чисел (хі, уi), і = 1...n…
При застосуванні цього критерію будується спільний варіаційний ряд. Спочатку визначається медіана для цього ряду. Якщо кількість значень непарна, то як медіана використовується середній елемент. Якщо кількість парна, медіана перебуває між 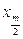 i
i 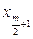 обчислюється за формулою:
обчислюється за формулою:
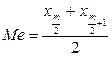
Після обчислення медіани визначається знак відхилення поточного значення хi, і = 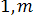 , від медіани. У такий спосіб одержують послідовність знаків, що розпадається на окремі серії — знаків одного виду, укладених між знаками іншого виду.
, від медіани. У такий спосіб одержують послідовність знаків, що розпадається на окремі серії — знаків одного виду, укладених між знаками іншого виду.
Приклад. +++---+----+++ -. Кількість серій r = 6.
За спеціальними таблицями для відомих значень кількості спостережень у вибірках N1 і N2 визначається для певного рівня статистичної значущості α 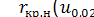 і
і 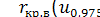 Якщо виконується співвідношення
Якщо виконується співвідношення
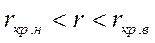
гіпотеза про належність вибірок до однієї генеральної сукупності, для якої FX(х) = FY(х), приймається, у протилежному разі — відхиляється.
Критерій знаків набув поширення в дослідницьких роботах завдяки тому, що процедура його застосування винятково проста, вимірювання ознаки, що враховується, можуть виконуватися грубими засобами, тому що має значення лише знак різниці результатів вимірювань, а в основу критерію покладені прості положення, яких майже завжди дотримуються (наприклад, не припускають нормального розподілу досліджуваних величин).
Питання для самоперевірки
1. Які критерії називаються непараметричними?
2. Яка гіпотеза перевіряється за допомогою критерію Уїлкоксона?
3. Що таке інверсія і як вона визначається?
4. Як двома способами за допомогою критерію Уїлкоксона перевірити правильність гіпотези?
5. Як визначається критичне значення й критична область для критерію Уїлкоксона?
6. Що таке медіана? Як вона визначається для вибіркових значень?
7. Що таке серія знаків та як вона визначається?
8. Як визначаються критичне значення та критична область для критерію знаків?
2.6 Перевірка гіпотез відносно частки ознаки порівняння двох вибірок
Критерії цієї групи дають змогу використовувати частку ознак і приймати рішення про властивість генеральної сукупності та відповідність нормам.
Будемо розглядати задачі: порівняння частки ознаки з нормативним значенням (стандартом) та порівняння частки ознаки у двох сукупностях.
Порівняння частки ознаки з нормативним значенням. Нехай потрібно перевірити гіпотезу, що частка р деякої ознаки у генеральній сукупності дорівнює деякому нормативному значенню α, тобто висувається нуль-гіпотеза Н0: р = α при альтернативній гіпотезі Н1: р≠α. Для перевірки гіпотези Н0 застосовують двобічний критерій, оскільки порушення гіпотези Н0 може бути як у разі р > α, так і в разі р < α. Як критерій застосовуємо статистику
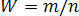
де n — загальна кількість випробувань; m — кількість позитивних результатів, W — частота.
Ця статистика при будь-якому n розподілена за біноміальним (для вибірки з поверненням) або за гіпергеометричним (для вибірки без повернення) законом розподілу. Однак при достатньо великому n при розрахунках можна скористатися асимптотичними розподілами, найчастіше — нормальним.
Виходячи з нормального закону розподілу при заданому рівні значущості α значення z знаходять із таблиць нормального розподілу згідно з рівністю:
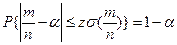
Узявши до уваги, що для біноміального закону 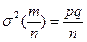 а також, що q=1 -р і для розглянутого випадку вихідним припущенням p =α, дістанемо вираз
а також, що q=1 -р і для розглянутого випадку вихідним припущенням p =α, дістанемо вираз
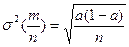
який надалі можна використати для знаходження надійних меж для W. Критичні точки в цьому випадку

Якщо вибіркова частість W буде в межах [W1, W2], гіпотеза H0 приймається.
У випадку, коли перевіряють альтернативну гіпотезу Н1: р>α, використовують однобічну критичну область із граничним значенням z згідно з рівнянням

Приклад. Перевіряється внесок деякого компонента до складу продукції.
1. Перевірити відповідність вкладу складової 10%-ному стандартному значенню, тобто перевірити гіпотезу H0: р = 0,1.
2. Перевірити, що наявність цього компонента у продукції не перевищує 10%, тобто перевірити гіпотезу Н1: р>α.
Порівняння частки ознаки у двох сукупностях. Припустимо, що маємо m1/n1 та m2/n2 частки однієї ознаки у двох сукупностях з n1 та n2 одиниць. Висувається гіпотеза H0: розбіжність між m1/n1 та m2/n2 є результатом впливу випадкових факторів та обмеженого обсягу вибірок.
Розглянемо випадок великих вибірок. Якщо n1 та n2 більші за 30, то розподіл вибіркових частостей при виконанні припущення про нульову розбіжність буде близьким до нормального з параметрами
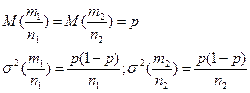
Для перевірки гіпотези застосовують статистику

Статистика W також може бути подана за допомогою нормального закону з параметрами
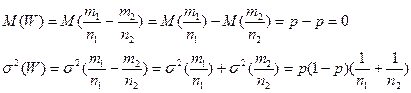
Для перевірки гіпотези H0 будемо використовувати двобічний критерій. Задаючись рівнем значущості α, знаходимо z згідно з рівнянням
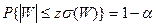
а потім визначимо критичні точки
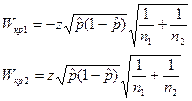
де 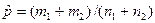 — оцінка p, яку отримують на підставі наявних даних двох вибірок.
— оцінка p, яку отримують на підставі наявних даних двох вибірок.
Якщо вибіркове значення W вміститься в інтервалі [Wкр1, Wкр2], то гіпотеза про несуттєвість розбіжності приймається.
Розглянемо випадок малих вибірок. Якщо n1 та n2 - малі числа, то використання нормального розподілу для статистики 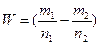 є хибним. У цьому випадку необхідно використовувати критерій χ2 за допомогою якого, як було показано раніше, при ідентифікації законів розподілу можна визначити розбіжність між теоретичними і вибірковими частками.
є хибним. У цьому випадку необхідно використовувати критерій χ2 за допомогою якого, як було показано раніше, при ідентифікації законів розподілу можна визначити розбіжність між теоретичними і вибірковими частками.
Для розглянутого випадку χ2 обчислюється в такий спосіб. Припустимо, що нас цікавить деяка ознака А. Беруть дві сукупності обсягами n1 та n2 і результати для позитивних А і негативних  наслідків заносять у табл. 2.1.
наслідків заносять у табл. 2.1.
У таблиці  1, і
1, і  2 — кількість елементів у кожній вибірці, які це мають ознаки А. Виходячи з припущення, що вибірки взято з тієї самої генеральної сукупності з часткою ознаки р, можна визначити теоретичні частоти, які відповідають фактичним частотам pn1, (1-p)n1, pn2, (1-p)n2.
2 — кількість елементів у кожній вибірці, які це мають ознаки А. Виходячи з припущення, що вибірки взято з тієї самої генеральної сукупності з часткою ознаки р, можна визначити теоретичні частоти, які відповідають фактичним частотам pn1, (1-p)n1, pn2, (1-p)n2.
Таблиця 2.1
| Сукупність | Фактичні частоти | Оцінки теоретичних частот | |||
| А | 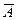
| Усього | А | 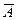
| |
| Вибірка 1 | m1 | 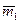
| n1 | pn1 | (1-p)n1 |
| Вибірка 2 | m2 | 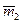
| n2 | pn2 | (1-p)n2 |
| Усього | m1+ m2 | 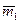 + + 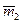
| n1+ n2 | -- | -- |
В останніх двох рядках табл. 19.1 наведені оцінки теоретичних частот, де замість р використовується  = (m1, +m2)/(nІ + n2).
= (m1, +m2)/(nІ + n2).
На підставі даних, наведених у табл. 19.1, можна обчислити χ2 за формулою:
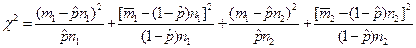
де у знаменниках записано оцінки відповідних дисперсій.
Беручи до уваги, що між чотирма теоретичними частотами існує три незалежні співвідношення, у розподілі χ2 необхідно враховувати тільки один ступінь свободи.
Якщо нульова гіпотеза, відповідно до якої обидві сукупності є вибірками з однієї генеральної сукупності, правильна, то розбіжність між теоретичними та дослідними частотами можна віднести тільки на рахунок випадкового відбору. Тому, визначивши для рівня значущості α значення χ2, приймемо рішення про відхилення гіпотези H0, якщо 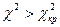 , незначущість розбіжності при
, незначущість розбіжності при 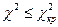 .
.
Приклад. Проводились випробування нового методу лікування. Одна група (експериментальна) — з 50 осіб (n1 = 50) лікувалася за новим методом, а друга («традиційна»), яка складалася з 30 осіб (n2 = 30), — за традиційним методом. Після завершення лікування у першій групі залишилося 9 хворих (m1=9), а в другій — 7 (m2=7). Необхідно перевірити суттєвість ефективності нового методу.
Обчислимо оцінку теоретичної частоти хворих після лікування:
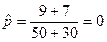
Позначимо позитивний результат для хворого — «вилікувалися за зазначений період» як подію А, тоді — «залишилися хворими» буде  . Вихідні дані та отримані результати наведено в табл. 2.2.
. Вихідні дані та отримані результати наведено в табл. 2.2.
Таблиця 2.2
| Групи, що обстежуються | Результати досліджень | Усього | Теоретичні результати | ||
| А | 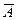
| А | 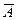
| ||
| Експериментальна | |||||
| «Традиційна» | |||||
| Усього: |
Розрахунок теоретичної кількості позитивних результатів будемо проводити відповідно за виразами 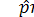 та
та 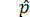 . Внесемо у табл. 19.2 оцінку
. Внесемо у табл. 19.2 оцінку  теоретичної кількості А та
теоретичної кількості А та  . Виходячи з даних, наведених у табл. 19.2, обчислимо значення критерію:
. Виходячи з даних, наведених у табл. 19.2, обчислимо значення критерію:
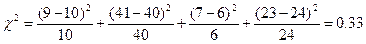
Скориставшись таблицями розподілу χ2, для α= 0,05 та ступеня свободи f =1, знайдемо критичне значення χ2кр =3,8. Таким чином, 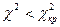 , тобто робимо висновок, що розбіжність частки хворих, які залишилися в обох групах після закінчення терміну лікування, не значуща, а отже, новий метод лікування дає такий самий ефект, як і традиційний.
, тобто робимо висновок, що розбіжність частки хворих, які залишилися в обох групах після закінчення терміну лікування, не значуща, а отже, новий метод лікування дає такий самий ефект, як і традиційний.
Порівняння двох залежних вибірок (парні зіставлення). У практиці статистичної перевірки гіпотез часто трапляються випадки, коли дві вибірки, які порівнюються, не можуть розглядатися як незалежні.
Приклад. Перевірка ефективності нової технології за результатами роботи тієї самої бригади до і після впровадження нової технології.
Приклад. Оцінка стану хворих до і після прийняття нових ліків. Проводячи реєстрацію по кожному об'єкту спостережень до нововведення — х і після нього —у, дістаємо два ряди спостережень:
| x1 | x2 | … | xi | … | xn |
| y1 | y2 | … | yi | … | yn |
Таким чином, ідеться про парні спостереження, тобто про n зв'язаних пар (хi, уi). Якщо досліджуваний фактор впливає тільки на одну з ознак х або у, то між цими парами спостережень фіксуватиметься суттєва розбіжність. Завдання полягає в тому, щоб визначити, коли розбіжність між парами спостережень можна віднести на рахунок випадкових відхилень, а коли вона суттєва і її потрібно пов'язувати з впливом якогось фактору.
Нехай різниця між спостереженнями в кожній парі становить 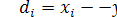 Тоді узагальненою величиною розбіжності пар спостережень може бути середня різниця
Тоді узагальненою величиною розбіжності пар спостережень може бути середня різниця
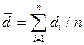 (2.21)
(2.21)
Чим менша різниця  , тим більш правдоподібне припущення щодо несуттєвості розбіжності між рядами спостережень. Таким чином, перевірці підлягає гіпотеза H0:
, тим більш правдоподібне припущення щодо несуттєвості розбіжності між рядами спостережень. Таким чином, перевірці підлягає гіпотеза H0: 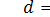 . Критерієм для перевірки може бути статистика
. Критерієм для перевірки може бути статистика
 (2.22)
(2.22)
де 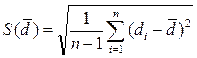
При нормальному розподілі різниць 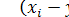 t -статистика має розподіл Стьюдента з кількістю ступенів свободи n - 1. Подальший механізм перевірки не відрізняється від перевірки розбіжності середніх.
t -статистика має розподіл Стьюдента з кількістю ступенів свободи n - 1. Подальший механізм перевірки не відрізняється від перевірки розбіжності середніх.
Перевірку гіпотез широко використовують у дисперсійному аналізі та в теорії кореляції, де перевіряють гіпотези про значущість відповідних параметрів, наявність стохастичного зв'язку, суттєвість впливу випадкових величин тощо.
Питання для самоперевірки
1. Чому при порівнянні частки ознаки з нормативним значенням використовують двобічний критерій?
2. Коли застосовують критерій χ2 при порівнянні частки ознак у двох сукупностях?
3. Який критерій застосовують при порівнянні двох залежних вибірок?
4. Чому при порівнянні частки ознак у двох сукупностях потрібно вводити чотири складові?
5. Як визначають оцінку теоретичної частки?
6. Коли застосовують парні спостереження?
Завдання планування експерименту
З постановкою і проведенням експериментів фактично пов’язана історія людства в цілому. Проте в більшос ті випадків ці роботи проводились хаотично на рівні інтуїції і попереднього досвіду, тому коефіцієнт корисної дії їх був досить низьким. Коли враховувати, що вартість одного досліду, як правило, висока, то не важко уявити, скільки коштувало людству проведення науково не спланованих експериментів. Особливо це важливо при дослідженні складних систем (а сучасні об’єкти практично всі є складними), поведінка яких залежить від великої кількості факторів.
Важливою умовою науково поставленого досліду є мінімізація загального числа дослідів (а значить, затрат матеріальних, трудових і часових), при цьому зменшення кількості дослідів не повинно суттєво відбитись на якості одержаної інформації.
При плануванні експерименту необхідно перш за все визначити мету експерименту і показники його якості, вказати характеристики плана і побудувати модель експерименту, вибрати критерії оптимальнос ті плану і встановити обмеження на показники якос ті дослідження. Організація і проведення експериментального дослідження потребує застосування особливих методів планування експерименту, тобто процедури вибору числа дослідів, необхідних і доступних для вирішення завдання з необхідною точністю і статистичною надійністю, умов постановки дослідів, методів математичної обробки результатів і методів теорії прийняття рішень.
Таким чином, після того як вибрана модель об’єкта і сформульована мета дослідження, треба спланувати експеримент, тобто: вибрати методи вимірювань і можливі типи засобів вимірювань; дати апріорну оцінку похибок вимірювань; сформулювати вимоги до метрологічних характерис тик засобів і умов вимірювань; вибрати засоби вимірювань відповідно до заданих вимог; вибрати параметри вимірювальної процедури; координати точок області експерименту, числа спостережень для кожної точки плану, моментів часу вимірювання, послідовності проходження точок плану; підготувати засоби вимірювання для проведення експерименту; забезпечити умови проведення експерименту. Експеримент необхідно реалізувати таким чином, щоб за мінімальною кількістю дослідів, варіюючи значення незалежних змінних за спеціально сформульованим правилом, побудувати математичну модель і знайти значення факторів, що забезпечують оптимальне функціонування системи. Простота і наявніс ть строгого математичного апарата, розробленого для моделі «чорний ящик», зумовили широке розповсюдження саме цього типу моделі.
Факторами називаються змінні величини, що приймають в деякий момент часу певне значення і відповідним чином діють на об’єкт. Факторами можуть бути як зовнішні для об’єкта впливи (температура., тиск, напруженіс ть магнітного і електричного полів, сила тяжіння, параметри джерела живлення та ін.), так і параметри самого об’єкта (опір, ємність та ін. параметри електричної схеми). Вибір факторів, параметрів оптимізації і моделей здійснюється з урахуваннями мети досліджень і умов для проведення експерименту. Кожний фактор може мати в досліді одне, або кілька значень, які називаються рівнями. Фіксований набір рівнів факторів визначає одне з можливих станів об’єкта, що досліджується, і відповідає визначеній точці багатомірного факторного простору.
Фактори можуть бути як кількісними, так і якісними.
Методика планування експерименту в більшості випадків потребує точної установки значень факторів, тому фактори повинні бути доступними вимірюванню з точністю на порядок вище, ніж точність вимірювання вихідної величини.
На різні набори рівнів система реагує по різному. Проте існує певний зв’язок між рівнями факторів і реакцією (відгуком) системи.
Вихідна величина в теорії планування експерименту залежно від завдань, що вирішуються, називається відгуком, функцією мети або параметром оптимізації. Серед множини вихідних величин дослідник повинен вміти виділити один параметр, який повинен допускати кількісну оцінку і для якого необхідно встановити функціональну залежність від рівнів факторів або який необхідно оптимізувати.
Date: 2015-09-19; view: 612; Нарушение авторских прав