
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Опосередковані вимірювання при нелінійній залежності
|
|
Загальним випадком опосередкованих вимірювань є їх опис нелінійним рівнянням, яке охоплює і опосередковані вимірювання при лінійній залежності. Для оцінки результату таких вимірювань використовують метод лінеаризації, який передбачає розклад нелінійної функції в ряд Тейлора. Для оцінки результату і похибки опосередкованих вимірювань знайдемо ефективні оцінки 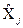 дійсних значень величин
дійсних значень величин 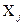 , вимірюваних прямими методами, тобто такі оцінки, які забезпечували б найменшу дисперсію, а отже, найбільшу точність результату опосередкованих вимірювань
, вимірюваних прямими методами, тобто такі оцінки, які забезпечували б найменшу дисперсію, а отже, найбільшу точність результату опосередкованих вимірювань 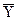 після підстановки оцінок
після підстановки оцінок 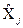 у нелінійне рівняння. Припускаючи, що в результатах прямих вимірювань присутні тільки випадкові похибки (систематичні похибки вилучені або враховані), отримаємо
у нелінійне рівняння. Припускаючи, що в результатах прямих вимірювань присутні тільки випадкові похибки (систематичні похибки вилучені або враховані), отримаємо
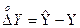 ;
;
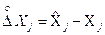 ,
,
де 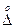 Y - абсолютна випадкова похибка оцінки
Y - абсолютна випадкова похибка оцінки 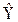 ;
;
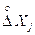 - абсолютна випадкова похибка оцінки
- абсолютна випадкова похибка оцінки 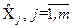 .
.
З урахуванням цих рівностей формулу (1.167) запишемо у вигляді:
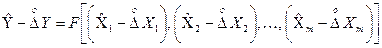 .
.
Це рівняння, зважаючи на те, що відносні випадкові похибки оцінок 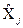 малі у порівнянні з одиницею, тобто
малі у порівнянні з одиницею, тобто 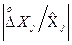 << 1, розкладають у m-мірний ряд Тейлора в точці
<< 1, розкладають у m-мірний ряд Тейлора в точці 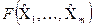 за степенями випадкових похибок
за степенями випадкових похибок 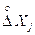 . Обмежимося першою і другою степенями розкладу (ряду)
. Обмежимося першою і другою степенями розкладу (ряду)
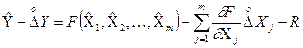 , (1.43)
, (1.43)
де 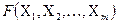 - нелінійна функціональна залежність вимірюваної величини Y від вимірюваних аргументів
- нелінійна функціональна залежність вимірюваної величини Y від вимірюваних аргументів 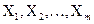 ;
;
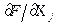 - перша похідна від функції F за аргументом
- перша похідна від функції F за аргументом 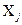 , яка обчислюється в точці
, яка обчислюється в точці 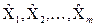 ;
;
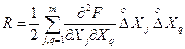 (1.44)
(1.44)
- залишковий член ряду.
Функція 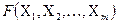 розкладена в ряд Тейлора у точці
розкладена в ряд Тейлора у точці 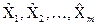 . Знак мінус перед сумою
. Знак мінус перед сумою 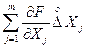 пояснюється тим, що абсолютна похибка за визначенням дорівнює
пояснюється тим, що абсолютна похибка за визначенням дорівнює 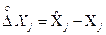 , а за правилом розкладу в ряд Тейлора повинно бути
, а за правилом розкладу в ряд Тейлора повинно бути 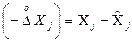 .
.
Метод лінеаризації застосовують, якщо приріст функції 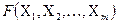 -
- 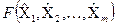 можна замінити її повним диференціалом
можна замінити її повним диференціалом 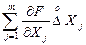 .
.
Оскільки перші члени правої і лівої частин виразу (1.170) не залежать від похибок, то їх можна подати наступними рівностями:
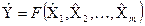 ; (1.45
; (1.45
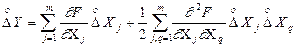 . (1.46)
. (1.46)
Таким чином, як випливає із рівняння (1.40), оцінку 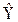 істинного значення Y фізичної величини при опосередкованих вимірюваннях отримують підстановкою в рівняння (1.40) оцінок
істинного значення Y фізичної величини при опосередкованих вимірюваннях отримують підстановкою в рівняння (1.40) оцінок 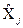 істинних значень
істинних значень 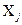 фізичних величин, вимірюваних прямими методами [20].
фізичних величин, вимірюваних прямими методами [20].
Залишковим членом R можна знехтувати за умови
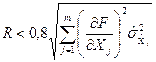 .
.
Проте на практиці ним, як правило, нехтують без перевірки цієї умови і залишають лінійні (за похибкою) члени ряду. І тільки в тому випадку, коли при оцінці похибки вони дають нульову оцінку, враховують квадратичні члени ряду.
Визначимо оцінку СКВ 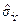 випадкової похибки
випадкової похибки 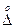 Y оцінки
Y оцінки 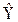 результату опосередкованих вимірювань, нехтуючи залишковим членом, тобто залишаючи тільки лінійні члени ряду:
результату опосередкованих вимірювань, нехтуючи залишковим членом, тобто залишаючи тільки лінійні члени ряду:
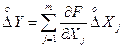 .
.
Використовуючи визначення дисперсії і основні властивості математичного сподівання, отримаємо:
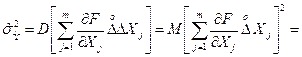
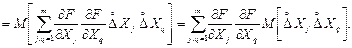 (1.47)
(1.47)
Для математичного сподівання добутку випадкових похибок 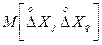 справедлива рівність
справедлива рівність
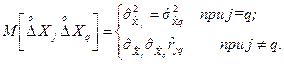
З врахуванням цього виразу формула (1.168) для дисперсії випадкової похибки результату опосередкованих вимірювань набуває вигляду
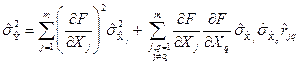 . (1.48)
. (1.48)
Частинні похідні 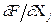 називають коефіцієнтами впливу, а величини
називають коефіцієнтами впливу, а величини 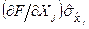 - частинними похибками опосередкованих вимірювань. Якщо ввести позначення
- частинними похибками опосередкованих вимірювань. Якщо ввести позначення 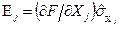 , то
, то
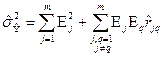 .
.
Оскільки коефіцієнти кореляції 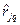 не залежать від значень оцінок
не залежать від значень оцінок 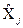 і
і 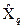 вимірюваних величин
вимірюваних величин 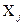 і
і 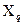 , то з виразу (1.175) випливає, що дисперсія оцінки
, то з виразу (1.175) випливає, що дисперсія оцінки 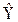 опосередкованих вимірювань досягає мінімуму в тому випадку, коли з можливих оцінок початкових величин вибрані ті, дисперсії яких мінімальні. Такими оцінками для величин, вимірюваних прямими методами з багаторазовими спостереженнями, є середні значення відповідних серій спостережень.
опосередкованих вимірювань досягає мінімуму в тому випадку, коли з можливих оцінок початкових величин вибрані ті, дисперсії яких мінімальні. Такими оцінками для величин, вимірюваних прямими методами з багаторазовими спостереженнями, є середні значення відповідних серій спостережень.
Отже, найбільш вірогідним значенням 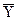 фізичної величини Y, вимірюваної опосередкованим методом, є значення, отримане з формули (1.46) після підстановки в неї середніх арифметичних значень
фізичної величини Y, вимірюваної опосередкованим методом, є значення, отримане з формули (1.46) після підстановки в неї середніх арифметичних значень 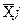 серій вимірювань початкових величин (або аргументів):
серій вимірювань початкових величин (або аргументів):
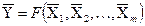 . (1.49)
. (1.49)
Оцінка СКВ результату опосередкованих вимірювань 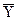 визначається за умови, що
визначається за умови, що 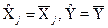 :
:
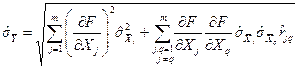 , (1.50)
, (1.50)
причому значення частинних похідних обчислюються при середніх арифметичних значеннях аргументів 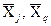 .
.
Якщо випадкові похибки вимірювань початкових величин 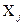 попарно некорельовані
попарно некорельовані 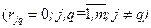 , то оцінка СКВ результату опосередкованих вимірювань (1.50) дорівнює сумі квадратів частинних похибок:
, то оцінка СКВ результату опосередкованих вимірювань (1.50) дорівнює сумі квадратів частинних похибок:
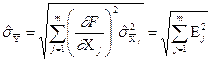 . (1.51)
. (1.51)
При прямих одноразових вимірюваннях формули (1.49)...(1.51) мають той самий вигляд, але в них треба провести формальну заміну: 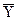 на Y,
на Y, 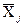 на
на 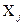 ,
, 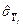 на
на 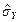 ,
, 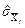 на
на 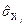 і
і 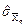 на
на 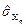 .
.
Проведемо зіставлення похибки і невизначеності опосередкованих вимірювань. Формули для СКВ похибки опосередкованих вимірювань (1.50), (1.51) одночасно визначають сумарну стандартну невизначеність таких вимірювань відповідно для корельованих і некорельованих вимірюваних величин 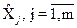 . У цих формулах можуть використовуватися стандартні невизначеності типу А (для яких вони приведені) і стандартні невизначеності типу В.
. У цих формулах можуть використовуватися стандартні невизначеності типу А (для яких вони приведені) і стандартні невизначеності типу В.
В свою чергу, через сумарну стандартну невизначеність обчислюється розширена невизначеність вимірювань, яка є інтервальною оцінкою, за формулою:
U = kouc,
де U - розширена невизначеність вимірювань;
uc - сумарна стандартна невизначеність вимірювань, зокрема 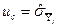 або
або 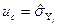 ;
;
ko - коефіцієнт охоплення, тобто числовий коефіцієнт, що використовується як множник сумарної стандартної невизначеності для визначення розширеної невизначеності [24].
У загальному випадку коефіцієнт охоплення вибирають згідно з рівністю
ko = tP(ks еф),
де tP(ks еф) - коефіцієнт Стьюдента, який залежить від ефективного числа степенів свободи ks еф та довірчої ймовірності Р.
Для більшості практичних задач число степенів вільності ks еф знаходиться в інтервалі 1,5...3,0. Так, для нормального закону розподілу можливих значень вимірюваної величини вважають ks еф = 2 при Р=0,95 і ks еф = 3 при Р = 0,99; для рівномірного розподілу ks еф = 1,65 при Р = 0,95 і ks еф = 1,71 при Р = 0,99.
Date: 2015-09-19; view: 542; Нарушение авторских прав