Оцінка результатів і похибок сумісних та сукупних вимірювань

Загальною ознакою сумісних і сукупних вимірювань, відповідно до їх визначення, є те, що значення шуканих величин отримують як розв’язок системи рівнянь, які пов’язують шукані величини з деякими іншими величинами, вимірюваними прямими або опосередкованими методами. Причому вимірюють декілька комбінацій значень цих величин. Вимірювання, проведені для кожної комбінації, дозволяють одержати одне рівняння, а сукупність цих рівнянь для всіх комбінацій являє собою систему рівнянь, в яку входять також усі значення шуканих величин [58].

При сукупних та сумісних вимірюваннях невідомі величини х_і, що підлягають безпосередньому вимірюванню, визначають за результатами вимірювання інших величин, які функціонально пов'язані з ними

φ(х₁, х₂,..., х _п) = y_j, (1.75)

де і = 1,2,.., п - порядковий номер невідомих величин х; j = 1,2,.., m - порядковий номер прямих вимірювань величин у.

Якщо результати прямих вимірювань Y містять випадкові похибки, то вони мають місце і в результатах сукупних (сумісних) вимірювань величин х_i. Розглянемо три випадки.

1.Очевидно, що для т < п систему розв'язати неможливо.

2.Для т = п розв'язання можливе, але похибки результатів вимірювання величин х_i будуть, як і для прямих одноразових вимірювань, значними, і числові значення цих похибок залишаються невідомими.

З.Для т > п систему знову неможливо розв'язати алгебрично, оскільки ці рівняння несумісні, так як праві частини рівнянь замість точних значень Y_i містять результати їхніх вимірювань у_i = Y_i + ΔΥ_i із випадковими похибками ΔΥ_i.

Проте в останньому випадку для нормального закону розподілу похибок вимірювання величини у_i можна знайти таку сукупність значень х, яка з найбільшою ймовірністю задовільняла б початкові умови φ(x₁,х₂,...,х _п) = у_i. Це можна здійснити за допомогою методу найменших квадратів (принципу Лежандра).

Такий спосіб обробки експериментальних даних для сукупних (сумісних) вимірювань доцільно застосовувати для лінійних функцій. В інших випадках обробка результатів значно ускладнюється.

Тому розглянемо випадок, коли функції φ_j лінійні

(1.76)

Представимо систему більш компактно:

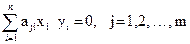. (1.77)

Тут індекси при коефіцієнтах а показані у послідовності «рядок-стовпець».

Ці рівняння називають умовними. Через наявність похибок праві частини рівнянь дорівнюють не нулю, а деяким залишковим похибкам:

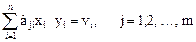. (1.78)

Згідно з принципом Лежандра, найбільш імовірними значеннями невідо­мих величин х_i для цього випадку будуть такі, для яких сума квадратів залишкових похибок 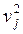мінімальна

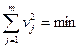. (1.79)

Необхідною умовою такого мінімуму повинна бути рівність нулю похідних

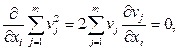і = 1, 2,..., n. (1.80)

Підставивши в останню формулу значення v _i, отримують систему нормальних рівнянь

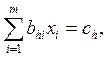h = 1, 2, …, n, (1.81)

яку в розгорнутому вигляді представляють наступним чином

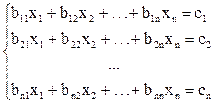(1.82)

Індекси при коефіцієнтах b показані в послідовності «рядок-стовпець» (h - і).

Оскільки кількість нормальних рівнянь завжди дорівнює кількості невідомих, то така система має розв'язок.

Методика отримання системи нормальних рівнянь полягає у знаходженні часткових похибок від кожної v _j по кожній з невідомих х_i шляхом перемноженням цих похідних на відповідні значення v _j та додаванні їх для кожної невідомої х_і

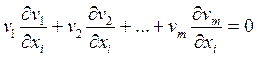(1.83)

Сукупність даних виразів представляє собою систему з п нормальних рівнянь.

Визначемо нормальні рівняння для n = 2.

Припустимо, що в результаті сукупних (сумісних) вимірювань отримано систему

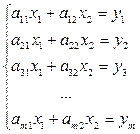(1.84)

Система нормальних рівнянь матиме вигляд:

(1.85)

Коефіцієнти b_hi визначають з виразів

b₁₁ = 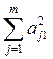; b₁₂ = b₂₁ = 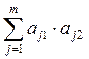; b₂₂ =

Тоді значення c_h визначають

c₁ = 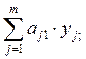c₂ =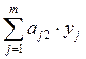

Розв’язок системи нормальних рівнянь проводиться наступним чином.

Якщо кількість невідомих п ≤ 4, то систему нормальних рівнянь доцільно розв'язувати за допомогою визначників. Розглянемо розв'язок систем нормальних рівнянь для п = 2.

У цьому випадку складаємо та обчислюємо головний визначник цієї системи рівнянь

D = 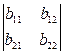(1.86)

Далі складаємо та обчислюємо часткові визначники D₁ та D₂, замінивши коефіцієнти b при відповідних невідомих на вільні члени с в системі

D₁ = 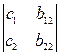, D₂ = .

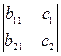Знаходимо найбільш імовірні значення невідомих

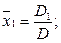
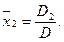
Середні квадратичні значення результатів сукупних (сумісних) вимірювань. Після підстановки найбільш імовірних значень х до умовних рівнянь

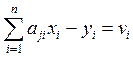, j = 1, 2, …, m, знаходимо значення залишкових похибок v _j, визначаємо v 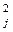та суму квадратів залишкових похибок .

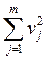Середнє квадратичне відхилення результатів сукупних (сумісних) знаходять за формулою

, (1.87)

де т - кількість умовних рівнянь; п - кількість невідомих; А_hi - ад'юнкти (алгебричні доповнення) елементів b_hi головної діагоналі визначника D (для h = і), які отримують викресленням h -го рядка та і -го стовпця, відповідних даному елементу b_hi, з наступним домноженям на (—1)^h+1.

Для п = 2 ад'юнкти: А₁₁ = b₂₂, А₂₂ = b₁₁.

Довірчі границі випадкової складової похибки сукупних (сумісних) вимірювань. Задавшись значенням довірчої ймовірності, знаходимо відповідне значення коефіцієнта довіри t_р. У цьому випадку число ступенів вільності дорівнює:

k = m – n; (1.88)

Довірчі границі випадкової похибки сукупних (сумісних) вимірювань становлять:

Δі = ± tр∙ S 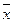(1.89)

Питання для самоперевірки

1. Як визначається вибіркове середньоквадратичне відхилення окремих результатів спостережень для вибірки

2. У якій послідовності відбувається обробка результатів одноразових прямих вимірювань?

3. Яка суть коефіцієнта кореляції t при статистичній обробці вибірок за умови нерівноточних вимірювань?

4. Як оцінюється похибка опосередкованого однократного вимірювання при нелінійній залежності між вимірюваною величиною і аргументами?

5. Що таке опосередковані вимірювання з багатократними спостереженнями аргументів?

6. В чому суть методу приведення при обробці результатів опосередкованих вимірювань з багатократними спостереженнями аргументів?

7. Які основні етапи мають місце при обробці результатів спостережень аргументів при опосередкованих вимірюваннях?

8. Які і як визначають оцінки результатів багатократних спостережень з нормальним законом розподілу при опосередкованих вимірюваннях?

9. Як впливає вид функціональної залежності на методику обробки результатів опосередкованих вимірювань?

Лекція №2

2 Статистична перевірка гіпотез

2.1 Поняття статистичної гіпотези. Припустима і критична області. Статистичний критерій

При опрацюванні випадко­вих величин на відміну від де­термінованих, можна зробити тільки припущення щодо їхньо­го походження, тобто висунути гіпотезу.

Статистичною гіпотезою називається будь-яке припущення щодо виду або властивостей роз­поділу спостережуваних в екс­перименті випадкових величин. Сутність перевірки статистичної гіпотези полягає в тому, щоб установити, узгоджуються чи ні ре­зультати спостережень та висунута гіпотеза, чи можна розбіжність між гіпотезою та результатом вибіркових спостережень віднести за рахунок похибки, зумовленої механізмом випадкового відбору.

Гіпотези бувають прості і складні.

Проста гіпотеза має тільки одне твердження.

Приклад. Параметр θ має одне конкретне значення (θ = θ₀).

Складна гіпотеза складається з безлічі простих гіпотез.

Приклад. Параметр θ має деяке значення із сукупності

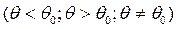
Гіпотезу, що висувають, називають основною гіпотезою. У зв'язку з тим, що вона найчастіше полягає у передбаченні відсутно­сті систематичної розбіжності (нульової розбіжності) між невідомим параметром генеральної сукупності й заданою величиною, то її також називають нульовою гіпотезою і позначають Н₀. Зміст гіпотези записують після двокрапки. Так, у розглянутому прикладі Н₀: θ = θ₀.

Зазвичай формулюють ще й альтернативну (конкуруючу) гіпотезу Н₁. У результаті перевірки можна приймати тільки одну з гіпотез Н₀ або Н₁, відхиляючи водночас іншу.

Гіпотезу перевіряють статистичними методами на підставі вибір­ки, отриманої з генеральної сукупності. Через випадковість відхилень значень у вибірці в результаті перевірки можуть виникати помилки й прийматися неправильне рішення. Коли рішення не відповідає спра­вжньому стану, можуть виникнути помилки двох видів.

Помилка першого роду має місце тоді, коли відхиляється пра­вильна гіпотеза Н₀.

Помилка другого роду полягає в тому, що приймається гіпотеза Н₀, коли правильною є альтернативна гіпотеза.

При перевірці гіпотез може виникнути одна із чотирьох ситуацій:

— гіпотеза Н₀ правильна й вона приймається;

— має місце гіпотеза Н₀, однак приймається неправильна гіпоте­за Н₁ (помилка першого роду);

— має місце гіпотеза Н₁, однак приймається неправильна гіпоте­за Н₀ (помилка другого роду);

— гіпотеза Н₁ правильна й вона приймається.

Здебільшого наслідки зазначених помилок нерівнозначні. Одна з помилок приводить до більш обережного, консервативного рішення, інша - до невиправданих дій. Що краще, що гірше — залежить від конкретної постановки задачі і змісту нульової гіпотези. Природним є прагнення зменшити втрати від обох помилок одночасно. Але, як ми побачимо далі, вони є конкуруючими, і зменшення ймовірності появи однієї з них призводить до збільшення ймовірності появи іншої. Таким чином, необхідно вибирати компромісне рішення. Ухвалення рішення грунтується на деякому статистичному критерії.

Статистичним критерієм називається певне правило обробки статистичного матеріалу (результатів дослідження), на підставі яко­го одна з гіпотез приймається, а всі інші відхиляються.

Кожен критерій має свою числову характеристику, що називається потужністю. Функцією потужності критерію називається ймовір­ність того, що основна гіпотеза Н₀ відхиляється, тоді як альтернативна гіпотеза приймається. Чим більша потужність критерію, тим менша ймовірність здійснення помилки 2-го роду.

Рішення приймається за значенням деякої функції вибірки, яка назива­ється статистикою, або статистичною характеристикою (z, t, χ²).

Для того щоб прийняти або відхилити передбачувану гіпотезу, потріб­но вибрати межу припустимих при висунутій гіпотезі відхилень від мате­матичного сподівання, тобто призначити таке критичне відхилення, пере­вищення якого при висунутій гіпотезі настільки малоймовірне, що його можна вважати практично неможливим. Якщо воно фактично спостеріга­лося, то це вказує на несумісність висунутої гіпотези з наявними спо­стереженнями, або якщо фактичне відхилення менше за критичну ме­жу, є підстави вважати, що результати досліду не суперечать висуну­тій гіпотезі, а спостережене відхилення від центра розподілу можна пояснити впливом випадкових величин.

Множину значень обраної статистики можна поділити на дві неперетинні підмножини:

—підмножина значень статистики, за якою гіпотеза Н₀ прийма­ється (не відхиляється), називається областю прийняття гіпотези (припустимою областю);

—підмножина значень статистики, за якою Н₀ відхиляється і приймається гіпотеза Н₁, називається критичною областю.

Критичними точками θ_кр називаються точки, які відокремлю­ють критичну область від припустимої. Критичні точки визначають за таблицями розподілу статистики.

Кількісно помилки оцінюють за ймовірністю їх виникнення.

Припустима ймовірність помилки першого роду позначається α (імовірність потрапляння статистичної характеристики в критичну область, тобто ймовірність практично неможливих відхилень) і на­зивається рівнем статистичної значущості.

Значення α зазвичай вибирається малим (0,05; 0,02; 0,01 — для технічних завдань; для завдань, пов'язаних із життям людини — 0,001).

Чим менший рівень значущості, тим менша ймовірність зробити помилку першого роду α, але тим вища ймовір­ність зробити помилку другого роду.

Для визначення критичної області статистики рівень значущості α вибирають з урахуванням виду альтернативної гіпотези Н₁.

Приклад. Основна гіпотеза Н₀: θ = θ₀. Альтернативна гіпотеза Н₁, може при цьому мати такий вигляд: Н₁:θ < θ₀; Н₁: θ > θ₀ або Н₁: θ ≠ θ₀. Відповідно можна дістати лівобічну (рис. 2.1, а), правобічну (рис. 2.1, б) або двобічну критичну область (рис. 2.1, в).

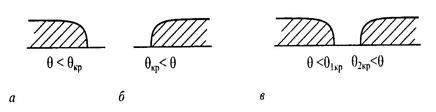
Рис. 2.1

Загальна схема перевірки статистичної гіпотези складається з таких етапів:

1. Формулюють гіпотези Н₀ і Н₁.

2. Вибирають статистику, за значенням якої приймається рішен­ня про правильність гіпотези. Необхідно, щоб статистика мала відо­мий закон розподілу.

3. Задаються рівнем статистичної значущості α.

4. Визначають критичні значення за таблицями а і вид альтернативної гіпотези Н₁.

5. Обчислюють за вибіркою значення обраної статистики.

6. Порівнюють значення обчисленої статистики з її критичним значенням.

7. Приймають рішення: якщо значення обчисленої статистики не потрапляє у критичну область, приймається гіпотеза Н₀ і відхиля­ється гіпотеза Н₁ і навпаки.

Питання для самоперевірки

1. Дайте означення статистичної гіпотези.

2. Яка гіпотеза називається нульовою?

3. Яка гіпотеза називається конкуруючою?

4. Яка гіпотеза називається простою, а яка - складною?

5. У чому полягають помилки першого та другого роду?

6. Що називається статистичним критерієм?

7. Що таке критична точка і як вона обирається?

8. Які значення величини містить критична область, а які — об­ласть прийняття гіпотези?

9. В яких випадках використовується лівобічна, правобічна та двобічна критичні області?

10. Який порядок перевірки гіпотез?

Date: 2015-09-19; view: 528; Нарушение авторских прав