Опрацювання результатів прямих нерівноточних вимірювань

У вимірювальній практиці іноді виникає потреба в обчисленні найдостовірнішого значення певної величини на основі вимірювань, здійснених із різною точністю (нерівноточні вимірювання). При знаходженні цього значення слід взяти до уваги точність результату кожного вимірювання, для чого вводиться поняття ваги g результату кожного вимірювання — це число, що є мірою ступеня довіри до результату цього вимірювання. Найдостовірнішим значенням вимірюваної величини при цьому вважається так зване середньозважене значення.

Якщо під час аналізу умов проведення вимірювання виявляється, що середні результати отримано за використання однакових приладів, але за неоднакової кількості спостережень, то можна вважати, що ваги середніх результатів пропорційні кількості спостережень для даного результату: 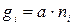g_і (тут а - будь-яке число).

Якщо ж ваги окремих результатів визначаються на основі порівняння загальних похибок цих результатів, то ваги їх можна обчислити за формулою

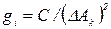(1.23)

Тут С —довільно вибране число; для полегшення обчислень доцільно взяти С таким, щоб усі g_і були по можливості цілими числами; ∆A_g - надійна межа загальної похибки середньозваженого результату, що обчислюється за формулою

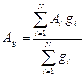(1.24)

де А_і — результати окремих вимірювань; g_i — вага, що характеризує точність і -го результату; N — кількість окремих результатів вимірювань.

Ваги результатів окремих вимірювань можна визначити двома способами:

• на основі аналізу всіх умов, за яких виконувалося вимірювання;

• на основі порівняння загальних похибок результатів окремих вимірювань.

При зіставленні результатів обробки двох вибірок можливі випадки взаємного перетину їх надійних інтервалів (наприклад, як зображено на рис.1.2). У такому разі треба з'ясувати, наскільки вірогідні відмінності між ними, чи вони настільки несуттєві, що обидві вибірки слід вважати приналежними до однієї й тієї самої генеральної сукупності.

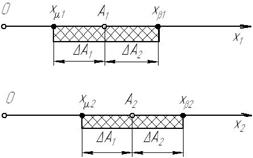
Рисунок 1.2 – Результати обробки двох вибірок

Припустімо, що є дві вибірки, кожну з яких можна вважати нормально розподіленою. Перша вибірка має параметри 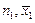та 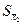, друга — відповідно 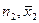та .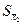

Необхідно обчислити значення коефіцієнта кореляції t за формулою

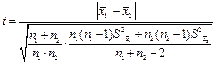(1.25)

Для обраної ймовірності Р та значення n (яке слід обчислити за формулою n = n₁+n₂ -1) в таблиці дод. 5 знаходимо t_g. Якщо t> t_g, то різниця між 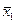та 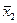є статистично вірогідною, і можна стверджувати, що ці вибірки належать до різних генеральних сукупностей. Якщо t 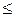t_g, то вибіркові середньоарифметичні 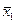та 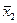відрізняються несуттєво, тобто ці обидві вибірки вилучені з однієї й тієї самої генеральної сукупності.

Якщо експериментально отримано сукупність значень х_і та у_і причому характер функціонального зв'язку між ними у=f(х) теоретично відомий, то обробка таких результатів вимірювань зводиться до обчислення параметрів функції, що найкраще відображає дану експериментальну залежність (таку функцію називають рівнянням регресії).

Цей метод особливо зручно використовувати для обробки експериментальних функціональних залежностей у випадку лінійного зв'язку між х та у. Рівняння лінійної регресії має такий загальний вигляд:

у=ax + b.

Обробка серії пар величин х_і та у_і дає змогу обчислити коефіцієнти лінійної регресії:

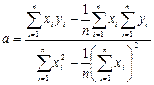(1.26)

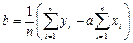. (1.27)

Тут n — кількість пар величин х_і та у_і у даному експерименті.

Для оцінки точності обробки результатів вимірювань треба обчислити середньоквадратичне значення відхилення експериментальних точок х_і, у_і від рівняння лінійної регресії; при цьому ширина смуги, що характеризує неточність результату (рис.1.3,а), дорівнює 2S_y(x).

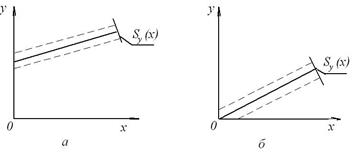
Рисунок 1.3 – Ширина смуги неточності результату

Для обчислення значення S_y(x) можна скористатися формулою:

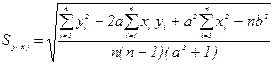(1.28)

В окремому випадку, коли відомо, що графік рівняння лілійної регресії проходить через нуль координатної системи (рис, 1.3,б), тобто це рівняння мас вигляд:

у=ах,

коефіцієнт а обчислюють за формулою:

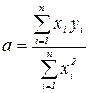, (1.29)

а середньоквадратичне значення відхилення:

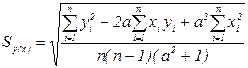. (1.30)

Date: 2015-09-19; view: 478; Нарушение авторских прав