
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Опрацювання результатів опосередкованих вимірювань з лінійною залежністю
|
|
Опосередковані вимірювання з лінійною залежністю у загальному випадку описують виразом:
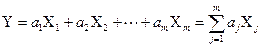 , (1.31)
, (1.31)
де 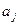 - постійні коефіцієнти при аргументах
- постійні коефіцієнти при аргументах 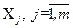 .
.
Якщо коефіцієнти 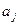 визначаються експериментально, то для знаходження результату опосередкованого вимірювання спочатку оцінюють кожний доданок
визначаються експериментально, то для знаходження результату опосередкованого вимірювання спочатку оцінюють кожний доданок 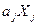 як опосередковану вимірювану величину, що являє собою добуток двох попередньо вимірюваних величин
як опосередковану вимірювану величину, що являє собою добуток двох попередньо вимірюваних величин 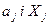 , а потім знаходять значення вимірюваної величини Y.
, а потім знаходять значення вимірюваної величини Y.
Для оцінки результату і похибки опосередкованих вимірювань використовуються основні властивості математичного сподівання (для оцінки результату вимірювання) і дисперсії (для оцінки СКВ похибки) суми випадкових величин. До уваги не приймають проміжні записи і припускають, що значення аргументів отримані прямими багаторазовими вимірюваннями, а похибки аргументів корельовані. В такому випадку:
- для результату опосередкованих вимірювань (тобто оцінки істинного значення опосередкованої вимірюваної величини) скористаємося формулою:
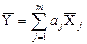 , (1.32)
, (1.32)
де 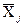 - середнє арифметичне значення j-го аргументу, одержане при обробці результатів прямих вимірювань величини
- середнє арифметичне значення j-го аргументу, одержане при обробці результатів прямих вимірювань величини 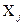 ;
;
- для оцінки СКВ результату опосередкованих вимірювань 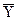 відомо:
відомо:
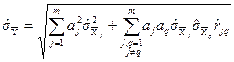 , (1.33)
, (1.33)
де 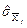 - оцінка СКВ результату вимірювання
- оцінка СКВ результату вимірювання 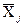 j-го аргументу;
j-го аргументу;
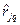 - оцінка коефіцієнта взаємної кореляції між випадковими похибками j-го і q-го аргументів (
- оцінка коефіцієнта взаємної кореляції між випадковими похибками j-го і q-го аргументів (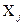 та
та 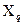 ).
).
У загальному випадку опосередкованих вимірювань, коли коефіцієнти 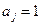 , з формул (1.32) і (1.33) відповідно маємо:
, з формул (1.32) і (1.33) відповідно маємо:
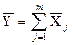 ;
;
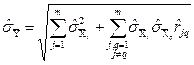 . (1.34)
. (1.34)
Критерієм відсутності кореляційного зв’язку між двома аргументами 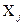 і
і 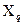 є виконання нерівності:
є виконання нерівності:
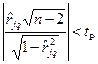 , (1.35)
, (1.35)
де 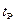 - коефіцієнт Стьюдента, що відповідає рівню значущості
- коефіцієнт Стьюдента, що відповідає рівню значущості 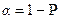 і числу степенів вільності ks = n - 2, причому n = min(
і числу степенів вільності ks = n - 2, причому n = min(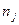 ,
, 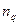 ) — найменше з чисел спостережень
) — найменше з чисел спостережень 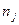 i
i 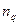 аргументів
аргументів 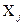 і
і 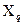 . Якщо вимірювана величина залежить від m аргументів, то перевіряють відсутність кореляційних зв’язків між усіма парними сполученнями цих аргументів.
. Якщо вимірювана величина залежить від m аргументів, то перевіряють відсутність кореляційних зв’язків між усіма парними сполученнями цих аргументів.
Оцінки коефіцієнтів кореляції 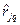 обчислюють за результатами прямих вимірювань аргументів (початкових величин)
обчислюють за результатами прямих вимірювань аргументів (початкових величин) 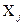 ,
, 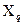 опосередкованих вимірювань.
опосередкованих вимірювань.
Наявність кореляції слід очікувати при вимірюваннях, де обидві фізичні величини (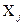 і
і 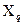 ) вимірюються одночасно за допомогою ЗВТ одного типу, а непомітні для експериментатора зміни зовнішніх дій (температури, напруги живлення, електричних і магнітних полів і т.д.) істотно й неоднаково впливають на додаткові похибки ЗВТ. Причиною кореляції між результатами вимірювань в окремих випадках може стати експериментатор, коли його навики і досвід значно впливають на результат прямих вимірювань початкових величин (при використанні ЗВТ з ручним зрівноважуванням).
) вимірюються одночасно за допомогою ЗВТ одного типу, а непомітні для експериментатора зміни зовнішніх дій (температури, напруги живлення, електричних і магнітних полів і т.д.) істотно й неоднаково впливають на додаткові похибки ЗВТ. Причиною кореляції між результатами вимірювань в окремих випадках може стати експериментатор, коли його навики і досвід значно впливають на результат прямих вимірювань початкових величин (при використанні ЗВТ з ручним зрівноважуванням).
При вимірюваннях, коли початкові величини вимірюють різними ЗВТ й у різний час, можна з достатньою впевненістю сказати, що результати цих вимірювань, якщо і будуть корельованими, то дуже слабко, і коефіцієнтом кореляції в (1.33) можна знехтувати, тобто вимірювання можна вважати незалежними. В цьому випадку формула (1.33) набуває вигляду:
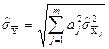 , (1.36)
, (1.36)
а при 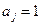
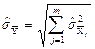 . (1.37)
. (1.37)
Розподіл результатів опосередкованих вимірювань буде нормальним, якщо нормальним є розподіл результатів прямих вимірювань. Тоді для визначення довірчого інтервалу результатів опосередкованих вимірювань використовується розподіл Стьюдента, при якому замість числа вимірювань n необхідно скористатися деяким «ефективним» числом степенів вільності, що в загальному випадку (при 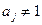 ) визначається за формулою
) визначається за формулою
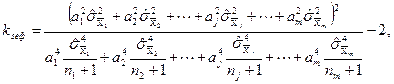
(1.38)
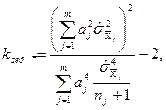
де 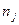 — число прямих спостережень у серії при визначенні
— число прямих спостережень у серії при визначенні 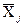 .
.
Якщо числа спостережень однакові 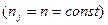 , то вираз для «ефективного» числа степенів вільності розподілу Стьюдента спрощується
, то вираз для «ефективного» числа степенів вільності розподілу Стьюдента спрощується
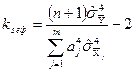 , (1.39)
, (1.39)
За умови, що розподіли похибок результатів вимірювань аргументів не суперечать нормальному розподілу, довірчі границі випадкової похибки результату опосередкованого вимірювання обчислюють за формулою [17]:
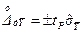 , (1.40)
, (1.40)
де 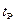 - коефіцієнт Стьюдента, що відповідає довірчій ймовірності і числу степенів вільності
- коефіцієнт Стьюдента, що відповідає довірчій ймовірності і числу степенів вільності 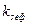 .
.
Невилучена систематична похибка опосередкованих вимірювань, якщо така похибка присутня в результатах вимірювань аргументів, оцінюється за даною методикою, при цьому важливі два випадки.
У першому випадку, коли невилучені систематичні похибки результатів вимірювань аргументів задаються границями 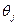 , довірчі границі невилученої систематичної похибки результату опосередкованих вимірювань
, довірчі границі невилученої систематичної похибки результату опосередкованих вимірювань 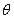 для довірчої ймовірності P знаходять за формулою
для довірчої ймовірності P знаходять за формулою
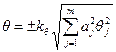 , (1.41)
, (1.41)
де 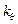 - поправочний коефіцієнт, що визначається довірчою ймовірністю P і числом m складових
- поправочний коефіцієнт, що визначається довірчою ймовірністю P і числом m складових 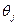 .
.
В другому випадку, коли невилучені систематичні похибки результатів вимірювань аргументів задаються довірчими границями 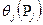 , що відповідають ймовірностям
, що відповідають ймовірностям 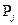 , і при тому границі невилученої систематичної похибки результату опосередкованого вимірювання для ймовірності P знаходять за формулою
, і при тому границі невилученої систематичної похибки результату опосередкованого вимірювання для ймовірності P знаходять за формулою
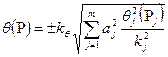 . (1.42)
. (1.42)
Значення коефіцієнтів 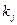 ,
, 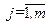 , та довірчу похибку результату опосередкованого вимірювання визначають математично.
, та довірчу похибку результату опосередкованого вимірювання визначають математично.
При прямих одноразових вимірюваннях формули (1.32)...(1.40) мають той самий вигляд, але в них треба провести формальну заміну: 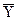 на
на 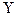 ,
, 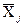 на
на 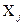 ,
, 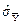 на
на 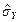 і
і 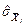 на
на 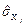 .
.
Date: 2015-09-19; view: 547; Нарушение авторских прав