Опрацювання результатів прямих одноразових вимірювань

Більшість вимірювань є однократними. В звичайних умовах їх точність достатня. Результат однократного вимірювання 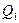записується наступним чином:

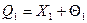, (1.1)

де 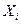- значення і-того показу; 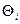- поправка.

Необхідною умовою проведення одноразового вимірювання служить наявність апріорної інформації. До неї відносять, наприклад, інформацію про вид закону розподілу ймовірності показів і міру його розсіювання, отриману із даних попередніх вимірювань. Такою інформацією може служити, наприклад, клас точності засобу вимірювальної техніки.

Оцінку похибки результатів вимірювання виконують при розробці методики виконання вимірювання. Джерелами виникнення похибок є модель об’єкта вимірювання, метод вимірювання, ЗВТ, оператор, фактори, що впливають на умови вимірювання, алгоритм обробки результатів вимірювання. Як правило, похибка результату вимірювання оцінюється при довірчій імовірності Р=0,95.

При виборі довірчої імовірності Р враховується степінь важливості результату вимірювання. Наприклад, якщо результат вимірювання пов’язаний з безпекою життєдіяльності людини, то значення довірчої імовірності Р повинно бути збільшене. За результат вимірювання в цьому випадку приймають результат однократного спостереження 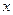(з введенням поправки, якщо вона є), використовуючи попередньо отримані (наприклад, при розробці методики виконання вимірювання) дані про джерела виникнення похибки.

Довірчі границі невиключеного залишку систематичної похибки результату вимірювання 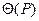обчислюють за формулою:

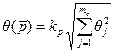, (1.2)

де 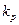- коефіцієнт, що визначається прийнятаю Р і числом m складових невиключеного залишку систематичної похибки, значення якого при Р=0,9 становить k(P)=0,95, а при Р=0,95 - k(P)=1,1 при будь-якому числі складових m; т _с – кількість складових систематичних похибок.

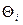– знайдені нестатистичними методами границі і-тої складової невиключеного залишка систематичної похибки.

При Р=0,99 значення k(P) визначається:

Якщо складові невиключеного залишку систематичної похибки розподілені рівномірно і задані довірчими границями 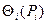, то довірчу границю результату вимірювання визначається за формулою:

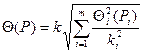, (1. 3)

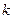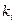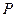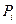де і – ті ж самі, що і в попередньому випадку, коефіцієнти довірчої імовірності і , відповідно; m – число складових невиключеного залишка систематичної похибки.

Середньоквадратичне відхилення результату вимірювання з однократним спостереженням обчислюють одним з наступних способів:

1) якщо в технічній документації на ЗВТ або в методиці виконання вимірювання вказані нормально розподілені складові випадкової похибки результата спостереження (інструментальна, методична, оператора, похибка, що виникає внаслідок дії різних чинників, і.т.д.), то СКВ визначають за формулою:

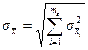, (1.4)

де т_в – кількість складових випадкових похибок.

Довірчу границю випадкової похибки результату однократного вимірювання знаходять за допомогою такої формули [24]:

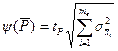, (1.5)

де 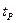-коефіцієнт довіри (коефіцієнт Стьюдента) з кількістю степенів вільності т_в -1 для відповідного значення довірчої ймовірності 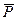, 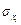- СКВ і -ї складової випадкової похибки.

2) якщо випадкові похибки задані довірчими границями, що відповідають одній і тій же довірчій ймовірності, то довірчу границю випадкової похибки результату однократного вимірювання знаходять за допомогою такого виразу:

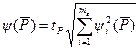. (1.6)

3) якщо довірчі ймовірності для складових є різними, то спочатку для кожної із складових розраховують СКВ 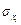за такою формулою:

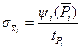, (1.7)

а потім використовується вираз (1.5).

При вимірюваннях з одноразовими спостереженнями окреме сумування систематичних та випадкових складових проводиться з метою порівняння між собою сумарної систематичної та випадкової складових похибки результату вимірювання. В результаті такого аналізу систематичних та випадкових складових та їх відповідного сумування отримують конкретне значення сумарної похибки однократного прямого вимірювання Δ_р.

Результат вимірювання з однократним спостереженнями записують у відповідності з вимогами методичних вказівок MИ 1317-86 „ГСИ”. Результаты и характеристики погрешностей измерений. Формы представления” в одній із таких форм:

, , ,

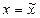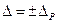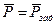або 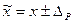, , 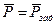(1.8)

де 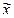– результат однократного вимірювання з урахуванням поправки 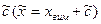, 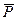_зад – прийняте значення довірчої ймовірності.

При цьому слід мати на увазі і дотримуватися таких основних правил запису:

1) похибку результату Δ_р вказують двома значущими цифрами, якщо перша з них дорівнює 1 або 2, і однією, якщо перша цифра 3 і більше;

2) результат вимірювання заокруглюють до такого десяткового розряду, яким закінчується заокруглене значення абсолютної похибки Δ_р;

3) заокруглення здійснюють лише в кінцевому записі, а всі попередні розрахунки здійснюють з одною-двома зайвими значущими цифрами.

Інші правила запису результатів вимірювання вказані у вище наведених методичних вказівках МИ 1317-86.

Одноразові вимірювання з наближеною оцінкою похибок характеризуються тим, що обробку даних проводять на основі апріорної інформації. До неї відноситься:

1) інформація про умови вимірювання,

2) інформація про методичні похибки,

3)інформація про метрологічні характеристики використовуваних засобів вимірювання.

Деколи в процесі вимірювання оцінюють (але не вимірюють) основні чинники, що впливають на вимірювальний процес. Таким чином, вхідні дані при обробці дозволяють оцінити похибки, але не дають можливості розрахувати та внести поправки в результат спостереження. В цьому полягає принципова відмінність даного виду вимірювання від попереднього.

За результат одноразового вимірювання приймають результат спостереження х_вим. Похибку результату оцінюють з урахуванням того, що для складових похибки відомі або визначаються границі, в межах яких допускається рівномірний розподіл складових. Це допущення обумовлене бажанням забезпечити можливість статистичного сумування складових похибок і тим, що на практиці реальні розподіли цих складових є невідомими.

Границі основної похибки Δ_р, яка допускається при даному виді вимірювання, відповідають вказаним у документації на засоби вимірювання. Границі для додаткових похибок знаходять на основі верхніх і нижніх границь, які можуть виникати за рахунок впливу відповідних чинників в процесі одноразового вимірювання. У загальному випадку отримуються несиметричні границі додаткових похибок θ_нj і θ_вj, j – впливаючий на процес одноразового вимірювання зовнішній чинник. Для спрощення процедури сумування складові похибки центрують, тобто представляють у формі:

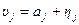, (1.9)

де 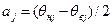– математичне сподівання додаткової j -ої похибки; η_j – випадкова складова додаткової j -ої похибки, яка має симетричні границі, модуль яких .

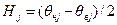Сума додаткових похибок у цьому випадку дорівнює:

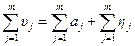, (1.10)

де т – кількість додаткових похибок засобу вимірювань.

Перший член у правій частині формули (1.151) знаходять алгебраїчним, а другий – статистичним сумуванням. Значення сумарної симетричної границі складових похибки знаходять так:

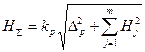, (1.11)

де k_p – коефіцієнт довіри.

Слід мати на увазі, що суму 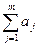не можна розглядати як поправку і виключати її з результату спостереження, так як оцінка складових є невисокою.

Одноразові вимірювання з апріорною оцінкою похибок відрізняються від розглянутих вище тим, що при підготовці до їх проведення надзвичайно важливою є апріорна інформація, зокрема, про вимірювану величину. Необхідно визначити діапазон можливих значень конкретної вимірюваної величини, так як від ширини цього діапазону залежить якість апріорної оцінки похибки результату вимірювання. Якщо вказаний діапазон не вдається знайти, то необхідно використати при оцінці похибки дані про діапазон вимірювання, взяті з нормативно-технічної документації на використовувані засоби вимірювання. При цьому, звичайно, отримана апріорна оцінка буде в багатьох випадках штучно завищеною. Для одержання більш реальної оцінки похибки її розраховують не в найменш сприятливій точці діапазону вимірювань, а в певній частині діапазону. Отримана таким чином оцінка буде справедлива для визначеної долі вимірюваної величини. З урахуванням зроблених зауважень алгоритм розрахунку границь похибки результату однократного вимірювання в цьому випадку залишається таким же, як і при вимірюваннях з наближеною оцінкою похибок. Аналогічною залишається також і форма запису результату вимірювання [29].

У виробничих умовах здебільшого проводять одноразові прямі вимірювання. При цьому робити висновок про точність результатів можна лише на підставі нормованих метрологічних характеристик засобів вимірювань. Для вимірювальних приладів такою метрологічною характеристикою є граничне значення допустимої основної похибки .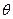

Обробку результатів одноразових прямих вимірювань слід здійснювати в такій послідовності:

- відкинути (або якомога зменшити) систематичну похибку;

- обчислити надійну межу похибки результату ∆А;

- записати результат вимірювання А, округливши його числове значення відповідно до значення надійної межі похибки ∆А (при цьому значення ∆А, як правило, не вказують).

Перевірка нормальності результатів вимірювань. З метою перевірки результатів спостережень на відповідність вибірки нормальному закону розподілу (або будь-якому іншому теоретичному закону розподілу) широке застосування знайшли такі критерії: критерій W, критерій 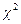(Пірсона), критерій Колмогорова-Смірнова.

Критерій 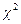(критерій Пірсона) дає можливість перевірити гіпотезу про відповідність вибірки результатів спостережень будь-якому теоретичному закону розподілу, а також перевірити на однорідність результати спостережень двох і більше вибірок.

При перевірці за допомогою критерію 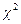однорідності довільної кількості вибірок L (L 2) кожну із вибірок х_jl,..., х_jn, де j =1,..., L; n_j – кількість результатів спостережень в j -ій вибірці, розбивають на класи по деякому признаку (r – загальна кількість класів), або груп по r інтервалах.

Розподіл даних по класах звичайно представляють у виді таблиці однорідності (табл.1.15). В цій таблиці через n_іj позначено кількість даних із j -ої вибірки, які ввійшли в і -ий клас, 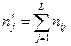– загальна кількість даних, які ввійшли в і -ий клас, 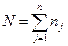– загальна кількість даних у всіх вибірках.

Якщо здійснюється групування, то рекомендується приймати інтервал однакової довжини (при N=100... 200 кількість інтервалів r =8... 12, при N=200...500 r =10... 15). Рекомендується критерій 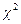використовувати, якщо загальна кількість даних N>40, класи даних не є досить вузькими: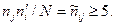

Значення статистики 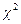розраховують таким чином:

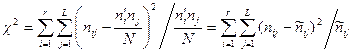. (1.12)

Досліджувані вибірки вважаються однорідними, якщо χ ²< χ ²_р, де χ ²_р– квантиль, χ ² – розподіл з f=(r-1)(L-1)степенями свободи.

При перевірці однорідності двох груп результатів спостережень із відповідно об’ємами цих спостережень п ₁ і п ₂ статистика 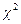розраховується за формулою

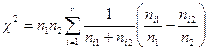. (1.13)

При цьому кількість степенем свободи f=r- 1.

Таблиця 1.1 – Перевірка гіпотези на однорідність L вибірок з розбиттям результатів спостережень на класи

Класи (інтервали)	Вибірки	Сума результатів у класі
l		j		L
l		...		...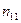
...	...		...		...
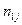
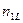
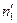
І		...		...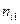
...	...		...		...
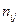
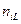
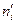
r		...		...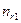
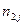
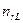
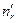
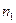
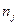
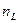
Об’єм вивірок		...		...		N

При використанні критерію 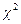для перевірки гіпотези рівність реального і теоретичного розподілів також здійснюють групування результатів спостережень п по r інтервалах. Причому мінімальна кількість інтервалів визначається так:

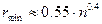, (1.14)

а максимальна кількість так:

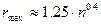. (1.15)

При п =100 (), ().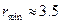

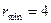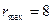Вибіркові частоти попадання результатів спостережень в і -ій інтервал т_і порівнюються із очікуваними частотами згідно теоретичного розподілу: 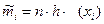, де h – ширина інтервалу, 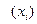– значення густини розподілу в центрі і -го інтервалу.

Значення статистики 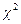розраховують по такій формулі:

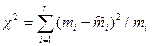. (1.16)

Якщо теоретичний розподіл був повністю заданий, то число степенем свободи з f=r- 1, якщо по вибірці оцінюється k її параметрів, то f=r-k -1 (зокрема, для нормального розподілу f=r-2 -1= r –3). Вважають, що вибірка із своїми результатами спостережень відповідає теоретичному розподілу, якщо χ ²< χ ²_р, де χ ²_р – квантиль χ ² – розподіл з f з степенями свободи, який також визначається згідно додатку А. При цьому значення довірчої ймовірності 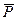можуть приймати значення від 0.01 до 0.99.

Критерій W дозволяє тільки перевірити вибірку результатів спостережень на її відповідність нормальному закону розподілу. Таку перевірку слід здійснювати після виключення із результатів спостережень систематичних похибок. Перевірка за допомогою критерію W здійснюється для вибірок об'ємом від 3 до 50 результатів спостережень.

Критерій Колмогорова-Смірнова дозволяє перевірити гіпотезу про приналежність даних вибірки до того чи іншого теоретичного закону розподілу; можна використовувати для п > 50.

Умовою проведення досліджень похибок, що виникають в результатах спостережень відповідної фізичної величини, є отримання цих результатів за допомогою засобів вимірювальної техніки при однакових зовнішніх умовах. Відсутність такої умови може привести до наявності часової залежності в результатах спостережень і, як наслідок, до суттєвого зменшення достовірності результатів їх обробки.

З метою виявлення часової залежності в результатах спостережень перед їх обробкою пропонується застосовувати R – критерій (методика перевірки відсутності часової залежності в результатах спостережень).

Date: 2015-09-19; view: 687; Нарушение авторских прав