Оцінка результату і похибки прямих багаторазових вимірювань

Постійно зростаючі вимоги до точності прямих вимірювань задовольняються не тільки за рахунок підвищення точності створених ЗВТ, але й використанням більш ефективних методів обробки результатів вимірювань, наприклад, статистичної обробки багаторазових вимірювань (або прямих вимірювань з багаторазовими спостереженнями).

Головна особливість багаторазових вимірювань, на відміну від одноразових, полягає в одержанні і використанні великого обсягу апостеріорної вимірювальної інформації. Це не означає, що необхідність в аналізі апріорної інформації відпадає. Такий аналіз обов’язково передує багаторазовому вимірюванню і має ту саму мету, що й при одноразових вимірюваннях, але з тією відмінністю, що при багаторазових вимірюваннях розподіл імовірностей їх результатів встановлюється експериментально. Визначення результату і похибки вимірювань з багаторазовими спостереженнями ґрунтується на статистичних оцінках або навпаки - статистичні оцінки одержують на підставі багаторазових рівноточних вимірювань. Методика обробки результатів прямих вимірювань з багаторазовими незалежними спостереженнями включає чотири основні етапи:

I. Аналіз апріорної інформації і підготовку до проведення багаторазових вимірювань.

II. Проведення вимірювання. Експериментально одержують n незалежних результатів спостережень вимірюваного розміру фізичної величини. Якщо зміною вимірюваної величини в часі можна знехтувати, то всі результати спостережень простіше за все одержати шляхом багаторазових (послідовних у часі) вимірювань даної величини тим самим ЗВТ. Якщо ж із апріорної інформації можна зробити висновок, що за час такої процедури вимірювана величина буде істотно змінюватися, то її вимірюють одночасно (паралельно) декількома ЗВТ, кожний з яких дає один із незалежних результатів спостережень. У цьому випадку дещо порушується одна з умов рівноточності вимірювань, але це вимушена операція і використовується досить рідко. Зменшити ефект від використання не одного, а декількох ЗВТ можна їх ретельним попереднім відбором.

За допомогою організації та планування експерименту в першу чергу вилучають або зменшують вплив відомих чинників, які призводять до систематичних похибок вимірювань. Якщо ці причини невідомі, то необхідно здебільшого експериментально (наприклад попередньою повіркою застосованих ЗВТ) або на підставі виявлення зовнішніх чинників одержати кількісну оцінку систематичної складової похибки вимірювань.

Результати проведеної серії спостережень при вимірюваннях позначимо 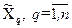. Відносно цих результатів спостережень зробимо два припущення. По-перше, будемо вважати, що вони підлягають нормальному розподілу (для підтвердження цього перевіряється гіпотеза про нормальність розподілу результатів спостережень), оскільки це найбільш розповсюджений на практиці випадок, для якого методи обробки експериментальних даних відпрацьовані. По-друге, вважають, що результати спостережень мають систематичну і випадкову складові похибки, тобто є невиправленими.

За одержаними експериментальними даними необхідно знайти результат вимірювання і оцінити його похибку. Вирішення цієї задачі зводиться до виконання операцій, умовно виділених у III і IV етапи методики.

III. Визначення результату прямих вимірювань з багаторазовими незалежними рівноточними спостереженнями.

1. З результатів спостережень 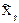вилучають, якщо це можливо, систематичну похибку введенням поправки і одержують виправлені результати спостережень .

Систематичні похибки (або їх залишки), які не можна вилучити в процесі експерименту та при обробці експериментальних даних введенням поправки, відносять до невилучених систематичних похибок і оцінюють їх як випадкові похибки при певних припущеннях.

2. За виправленими результатами спостережень X_q знаходять результат прямих багаторазових вимірювань, тобто оцінку вимірюваної величини. Така оцінка, одержана за експериментальними даними, вважається найкращою, якщо вона незміщена, обґрунтована та ефективна. Для експериментальних даних, які відповідають нормальному розподілу, найкращою статистичною оцінкою вимірюваної величини є середнє арифметичне 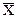, а найкращою оцінкою характеристики випадкової похибки – її СКВ.

IV. Обчислення оцінок характеристик похибки результату прямих вимірювань з багаторазовими спостереженнями.

1. Визначають незміщену оцінку СКВ 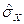результатів вимірювань, вводячи позначення 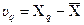. Величину 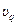називають залишковою похибкою або відхиленням q-го результату виправленого ряду спостережень від результату вимірювань (середнього арифметичного значення 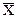) цього ряду спостережень. Інакше кажучи, відхилення , показують, наскільки результат 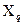кожного спостереження відрізняється від середнього арифметичного значення 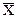, прийнятого за результат вимірювання, причому величини 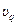можуть бути додатними або від’ємними. Очевидно, якщо відхилення 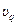дуже малі за модулем, то результати спостережень 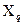близькі один до одного і можна вважати, що вимірювання досить точні. У протилежному випадку, коли хоча б частина відхилень 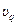має досить великі значення, вимірювання не такі вже й точні. З врахуванням рівності 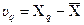, визначення оцінки СКВ 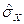зводиться до послідовного обчислення відхилень 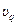, піднесення їх до квадрата, сумування цих квадратів і обчислення квадратного кореня із середнього значення отриманої суми квадратів. Для відхилень 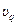справедливе рівняння , яке використовується для перевірки правильності їх обчислення [20].

2. Перевіряють гіпотезу про нормальність розподілу результатів, попередньо вилучивши з експериментального ряду спостережень результати, які є промахами. Якщо число спостережень 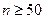, то застосовують критерій Пірсона (критерій 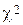), при 10 £ n < 50 використовують складений критерій. Рівень значущості при цьому вибирають з інтервалу (2...10) %. При числі спостережень 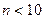нормальність розподілу їх результатів не перевіряється.

3. Якщо гіпотеза про нормальність розподілу результатів спостережень підтверджується, то визначають наявність грубих результатів. У тому випадку, коли грубі результати виявлені, вони відкидаються і для отриманого ряду обчислюють середнє арифметичне значення 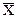і незміщену оцінку 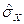результатів спостережень.

4. Визначають границі довірчого інтервалу похибки результату прямих багаторазових вимірювань. Для цього:

- знаходять границі довірчого інтервалу випадкової складової похибки;

- обчислюють границі довірчого інтервалу невилученої систематичної складової похибки, якщо вона є. До складових невилученої систематичної похибки можуть належати методична похибка і складові інструментальної похибки ЗВТ, якщо їхніми випадковими складовими можна знехтувати;

- обчислюють границі довірчого інтервалу сумарної похибки результату вимірювання.

5. Записують результат вимірювання. Якщо результат, одержаний при багаторазових вимірюваннях, призначається в подальшому для аналізу і зіставлення з іншими результатами або є проміжним для знаходження інших величин, то необхідно вказати окремо границі допустимої невилученої систематичної похибки і оцінку СКВ випадкової похибки вимірювань.

Інколи при великому числі результатів спостережень 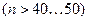для зменшення обсягу обчислень використовують групування даних, як і при побудові гістограми.

Очевидно, прямі одноразові вимірювання, для яких відома апріорна інформація про випадкову і невилучену систематичну складові похибки, можна вважати окремим випадком прямих багаторазових вимірювань. Тому і для тих, і для інших границі довірчих інтервалів окремих складових і повної похибки визначаються за однією тією ж методикою, однаково записується і результат вимірювань. Відмінність полягає тільки в тому, що при прямих одноразових вимірюваннях характеристики похибок відомі апріорно, а при багаторазових вимірюваннях їх одержують за експериментальними даними, тобто вони є апостеріорними.

Основна ідея багаторазових вимірювань того самого розміру вимірюваної величини полягає в переході від результату окремого вимірювання до середнього арифметичного значення 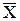ряду вимірювань. СКВ випадкової похибки, а отже, і границі довірчого інтервалу середнього арифметичного значення 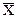в 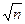разів менші, ніж ті самі величини для окремого вимірювання. Проте точність багаторазових вимірювань обмежується недостатністю експериментальної інформації і можливим часом її отримання.

Date: 2015-09-19; view: 535; Нарушение авторских прав