Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Средняя квадратическая ошибка функции ряда измеренных величин
|
|
Предположим, что искомую величину F мы находим как функцию ряда измеренных величин
F = f (x, y, z...t)
где x, y, z...t - результаты измерений, содержащие ошибки.
В математике доказывается, что главный член приращения функции, зависящий от малых приращений аргументов равен полному дифференциалу этой функции, то есть
(79)
, 
, 
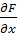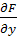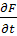- частные производные данной функции по соответствующим аргументам.
Предположим, что для искомой величины был выполнен бесконечно большее число циклов независимых измерений величин. Тогда для каждого цикла можно записать уравнение ошибок
.
.
.
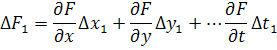
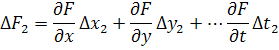
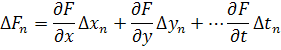
Чтобы избавиться от двойственности знаков ± у ошибок измерений, каждое из этих уравнений возведем в квадрат, затем сложим все уравнения и разделим на число измерений h. В итоге получаем
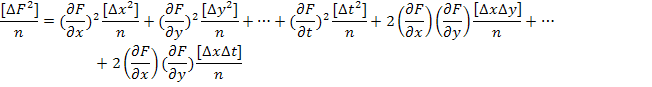
По четвертому свойству случайных ошибок последние, подчеркнутые, члены этой функции стремятся к нулю при неограниченном возрастании числа измерений. Поэтому средняя квадратическая ошибка функции ряда независимых измерений имеет вид (при независимых ошибках измерений)
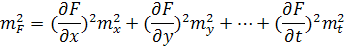(80)
Date: 2015-09-19; view: 614; Нарушение авторских прав