Классификация ошибок измерений

Из опыта известно, как бы точно не выполнялись многократные из­мерения одной и той же величины, результаты будут отличаться один от другого. Другими словами, измерения всегда сопровождаются ошибками -отклонениями измеренных величин от истинных значений.

∆=l-Х,

где ∆ - ошибка измерения, l - результат измерения, X - истинное зна­чение измеряемой величины.

В ошибках измерений можно выделить три части: грубую ошибку, систематическую и случайную.

Грубая часть ошибки появляется из-за невнимательности наблюдателя или при поломке инструмента, а также при резком ухудшении условий наблюдений. Причина возникновения грубой ошибки весьма существенна, поэтому исключить эту часть ошибки можно только повторными измерениями.

Анализируя оставшуюся часть ошибки в ней можно определить систематическую долю, которая остается неизменной при повторном измерении Эта часть ошибка имеет постоянный знак и величину и может быть исключена путем введения соответствующих поправок.

Нельзя исключить случайную ошибку, которая изменяется как случайная величина, но если знать законы распределения случайных ошибок, то можно контролировать их влияние.

Свойства случайных ошибок, выявленные на основе эмпирических исследований, помогают оценить точность измерений.

1. Свойство симметричности относительно нуля означает, что при выполнении равноточных измерений равно возможно появление случайных ошибок, равных по абсолютной величине и противоположных знаков.

2. Свойство компенсации является следствием свойства симметрич­ности и означает, что при равноточных измерениях сумма случайных оши­бок, деленная на их число, стремится к нулю при неограниченном возрас­тании числа измерений:

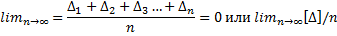
где п - число измерений, [] - знак суммы по Гауссу.

3. Свойство рассеивания означает, что при равноточных измерениях сумма квадратов случайных ошибок, деленная на их число стремится к не­которому пределу, постоянному для данных условий наблюдений, при не­ограниченном возрастании числа измерений:

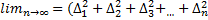)/n=σ² (72)

где σ² - дисперсия, а ∆_i -стандарт измерения является теоретическим критерием точности измерений. Третье свойство является очень важным для оценки точности выполненных измерений и широко используется на практике. Теоретический критерий заменяется значением средней квадра-тической ошибки, которая при наличии случайных ошибок определяется по формуле Гаусса

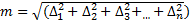/n= (73)

где п - число измерений ограничено, а ∆_i - случайные ошибки, вы­числяются по формуле

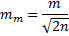(74)

4. Свойство ограничения - случайная ошибка измерений не может превышать некоторого предела, свойственного данным условиям измере­ний и называемого предельной ошибкой ∆ _пред. В теории ошибок для пре­дельной ошибки устанавливаются следующие значения ∆ _пред = 2т с веро­ятностью 0,95 и ∆ _пред =3т с вероятностью 0,997.

5. Свойство плотности - при равноточных измерениях, чем меньше по абсолютной величине ошибка, тем чаще она появляется.

Если случайные ошибки обладают этими свойствами, то они подчи­няются закону нормального распределения случайных ошибок измерений.

Кроме этого для ряда равноточных измерения с нормальным распределени­ем можно получить следующие виды ошибок.

Средняя ошибка ряда равноточных измерений, вычисляемая по фор­муле

J = [│∆│ /nи составляет примерно 4/5 от стандарта измерений.

Вероятная ошибка, по определению находящаяся в середине ряда, приблизительно равна 2/3 от стандарта измерений.

Если результат измерений зависит от размеров в измеряемой величины, то для характеристики точности измерений используется понятие относительной ошибки, т.е. отношение самой ошибки к результату измерений,например

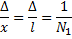относительная случайная ошибка,

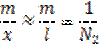относительная средняя квадратическая ошибка

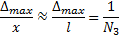относительная предельная ошибка.

Date: 2015-09-19; view: 540; Нарушение авторских прав