
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Обработка результатов неравноточных измерений
|
|
Измерения, выполненные в разных условиях, называются неравноточными. При неравноточных измерениях степень надежности каждого измерения различна. Для ее характеристики введено понятие веса измерения. Весом называют величину обратно пропорциональную квадрату средней квадратической ошибки измерения.
Так каждый результат измерения можно оценить его ошибкой и весом.
l1 ® m1, вес p1 = 1/m12; l2 ® m2, вес p2 = 1/m22
При сопоставления весов, для удобства расчета их можно увеличить или уменьшить в одинаковое число раз.
Так p1 = с: m12; p2 = c: m22 (c = const)
Например, если среднее арифметическое определяется из разного числа n1 и n2 равноточных измерений
L1 = [l] / n1, mL12 = m2 / n1, L2 = [l] / n2, mL22 = m2 / n2
p1 = n1 / m2, p2 = n2 / m2
где m - ошибка одного измерения, и если принять с = т2, то p1 = n1, p2 = n2 т.е. формально за вес простой арифметической средины можно принять число измерений, из которых она составлена. При определении искомой величины из ряда неравноточных измерений простое среднее арифметическое нельзя принять за наиболее надежный результат, так как к более точным измерениям нужно отнестись с большей степенью доверия. В этом случае нужно пользоваться формулой общей арифметической середины, вывод которой сделан на основе таких рассуждений.
Пусть дан ряд равноточных измерений, числом n
l1, l2....ln, L = [l]: n
Разобьем этот ряд на несколько неравных частей и из каждой его части составим свое среднее значение l / эти значения уже будут неравноточными
l1¢ = [l]1 / n1, l2¢ = [l]2 / n2, l3¢ = [l]3 / n3, n1 + n2 + n3 = n
тогда можно записать
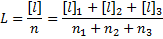
но [l]1 = l’1 * n1, [l]2 = l’2 * n2, [l]3 = l’3 * n3
а так как формально веса pi = niто
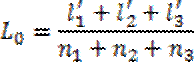 (86)
(86)
Эта формула называется формулой общей арифметической средины. Ею можно пользоваться и при равноточных измерениях, так как приняв в этом случае р = I, получим L1 = [l] / n 1 т.е. формула простой арифметической средины является частым случаем общей арифметической средины.
Пример. Один и тот же угол измеряется разными теодолитами результаты:
b1 = 15°32¢ 30², m1 = 20², p1 = 1/400
b2 = 15°32¢ 20², m2 = 10², p2 = 1/100
b3 = 15°32¢ 10², m3 = 5², p3 = 1/25
Пусть С = 400, тогда p1 = 1; p2 = 4; p3 = 16. Тогда вынося общую часть 15°32 за знак формулы, получаем
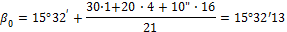
т.e. полученный результат, близкий к третьему точному результату измерений.
Найдем формулу веса общей арифметической средины
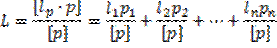 (87)
(87)
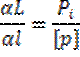 (88)
(88)
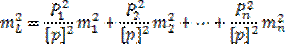 (89)
(89)
но, 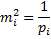
тогда mL2 = [p]/[p]2 = 1/[p], а вес PL = 1/mL2 = [p]
Тo есть, вес общей арифметической средины равен сумме весов слагаемых
измерений.
Свойство отклонений V от общей арифметической средины.
Пусть дан ряд измерений l1...ln с весами p1...pn
L = [l * p] / [p]
Составим уравнения отклонений
l1 – L = V1 * p1 = p1* l1 – p1 * L = p1 * V1
l2 – L = V2 * p2 = p2* l2 – p2 * L = p2 * V2
....................................................................
ln – L = Vn * pn = pn* ln – pn * L = pn * Vn
[p * l] - L* [p] = [p * V] = 0
Понятие об ошибке измерений, вес которой равен единице (ошибка единицы веса).
При неравноточных измерениях вместо ошибки одного измерения определяется средняя квадратическая ошибка m измерения, вес которой равен единице.
Если дан ряд измерений l1, l2...ln, с ошибками Di и весами рi то можно записать пропорции
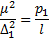
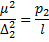
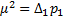
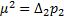
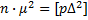 то
то 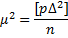 (90)
(90)
Если в ряде измерений получены отклонения V от общей арифметической средины, то
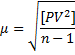 это обобщение формулы Бесселя (91)
это обобщение формулы Бесселя (91)
Поэтому средняя квадратическая ошибка общей арифметической средины вычисляется по формуле
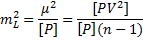 (92)
(92)
Date: 2015-09-19; view: 1321; Нарушение авторских прав