Две меры механического движения. Работа силы. Мощность

В динамике рассматриваются два случая преобразования механического движения материальной точки или системы точек:

1) механическое движение переносится с одной механической системы на другую;

2) механическое движение превращается в другую форму движения материи (в форму потенциальной энергии, теплоты, электричества и т.д.).

Каждый из этих случаев преобразования механического движения имеет свои измерители как механического движения, так и действия силы. Когда рассматривается преобразование механического движения без перехода его в другую форму движения, мерой механического движения является вектор количества движения материальной точки или механической системы .

Мерой действия силы в этом случае является вектор импульса силы . Когда механическое движение превращается в другую форму движения материи, в качестве меры механического движения выступает кинетическая энергия материальной точки или механической системы.

Из элементарного курса физики известно, что кинетическая энергия материальной точки массой 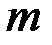,движущейся со скоростью 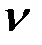, равна половине произведения массы этой точки на квадрат скорости ее движения:

. (8.7)

Работа силы. Мерой действия силы при превращении механического движения в другую форму движения является работа силы, которая также рассматривается в элементарном курсе физики.

В данном разделе рассмотрены различные случаи вычисления работы сил и сформулирована теорема об изменении кинетической энергии как материальной точки, так и механической системы.

Итак, существуют две различные меры механического движения: количество движения 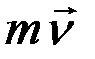и кинетическая энергия 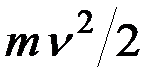– и две различные меры действия силы: импульс силы 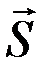и работа силы 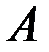. Следует отметить, что измерителями механического движения и действия силы в первом случае являются векторные величины и 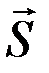,а во втором случае – скалярные величины 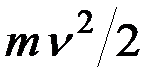и .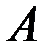

Так как изменение величины связано с работой приложенных к телу сил, то работа является количественной мерой превращения механического движения в какую-либо другую форму движения.

Рассмотрим сначала вычисление работы силы, постоянной по модулю и направлению, на прямолинейном перемещении её точки приложения. Предположим, что точка приложения постоянной силы 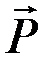перемещается по прямой из в 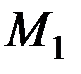(рис. 22), а вектор силы составляет с вектором перемещения 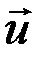угол .

Рис. 22

Работа силы в этом случае равна произведению модуля силы на длину пути, пройденного точкой приложения силы, и на косинус угла между направлениями вектора силы и вектора перемещения точки ее приложения:

. (8.8)

Если угол 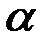острый, то работа силы положительна, а если тупой, то отрицательна; т.е. работа положительна, когда сила ускоряет движение, и отрицательна, когда она замедляет движение.

Из векторной алгебры известно, что скалярное произведение двух векторов равно

.

Следовательно, работа силы на перемещении равна

. (8.9)

Итак, работа постоянной по модулю и направлению силы на прямолинейном перемещении определяется скалярным произведением вектора силы на вектор перемещения точки её приложения.

Если направления силы и перемещения совпадают, т.е. 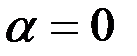, то

.

Если направление силы перпендикулярно направлению перемещения, т.е. 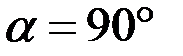, то

.

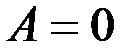Если направление силы противоположно направлению перемещения, т.е. 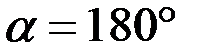, то

.

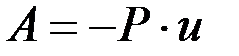Графический способ вычисления работы. Если сила зависит от расстояния S и известен график зависимости 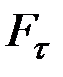от S ( 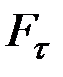– проекция вектора силы 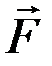на касательную к траектории движения точки), то работу силы можно вычислить графически. Пусть в положении 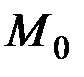точка находится от начала отсчета на расстоянии S ₀, а в положении 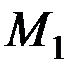– на расстоянии S ₁ (рис. 23). Тогда, учитывая геометрический смысл интеграла, получим:

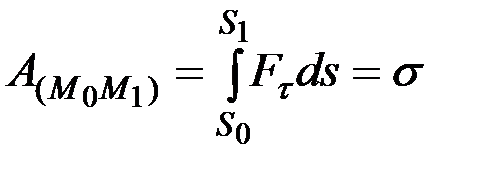, (8.10)

где – величина заштрихованной на рис. 23 площади, умноженной на масштабный коэффициент.

Рис. 23

Мощность. Мощностью называется величина, определяющая работу, совершаемую силой в единицу времени. Если работа совершается равномерно, то мощность

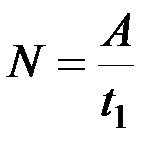, (8.11)

где 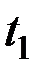– время, в течение которого произведена работа 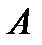.В общем случае

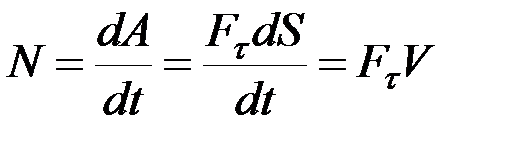. (8.12)

Следовательно, мощность равна произведению касательной составляющей силы на скорость движения.

Date: 2015-09-03; view: 1706; Нарушение авторских прав