Параметры торможения

В потоке жидкости могут существовать точки или области, скорость жидкости W в которых равна нулю. Это может быть критическая точка на поверхности обтекаемого тела, в которой по определению W=0. При истечении жидкости через отверстие или сопло из ёмкости большого объёма, жидкость внутри этой ёмкости практически везде, кроме области, непосредственно прилегающей к отверстию или соплу, можно считать неподвижной, принимая, что W=0.

Рассмотрим энергоизолированное течение жидкости вдоль линии тока между двумя точкам, в одной из которых скорость жидкости имела конечное значение (W>0), а в другой в результате торможения жидкость остановилась и её скорость стала равна нулю (W=0). Последнюю точку будем называть «точкой торможения» и все параметры жидкости в этой точке называть «параметрами торможения» и отмечать далее звёздочкой (*). Если исходить из одномерной постановки задачи, то нам надо рассматривать изменение параметров жидкости не строго на линии тока, соединяющей указанные точки, а в некоторой «окрестности» этой линии, т.е., по существу, в элементарной струйке. Запишем интегральное уравнение энергии для участка элементарной струйки, соответствующего рассматриваемому течению:

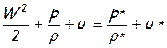или ,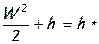

где удельная потенциальная энергия выражена через энтальпию жидкости .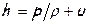

Поскольку в точке торможения кинетическая энергия жидкости полностью переходит в потенциальную (W®0), то в этой точке энтальпия h^* определяет уже не только потенциальную энергию, но и весь запас энергии единицы массы жидкости, т.е. её полную удельную энергию. Поэтому энтальпию в точке торможения или «энтальпию торможения» называют ещё «полной энтальпией».

В случае течения совершенного газа, который имеет постоянные теплоёмкости C_p и C_v, показатель адиабаты (изоэнтропы) 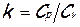, удовлетворяет уравнению состояния (уравнению Менделеева-Клапейрона) 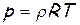, где удельная газовая постоянная 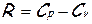, с учетом очевидного соотношения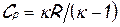 энтальпия может быть представлена следующим образом:

,

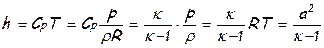где 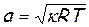- скорость звука.

Тогда уравнение энергии для элементарной струйки примет вид:

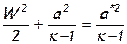или ,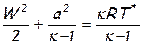

где a^* и T^* - соответственно скорость звука и температура в точке торможения или «температура торможения».

Если допустить, что процесс торможения жидкости является обратимым и, следовательно, энтропия жидкости S при этом не изменяется, т.е. торможение происходит в режиме, так называемого, «изоэнтропийного течения», то параметры жидкости, которые она будет иметь в результате такого торможения, принято называть «параметрами изоэнтропийного торможения». Условию изоэнтропийности (dS=0) полностью удовлетворяет только энергоизолированное течение идеальной жидкости, поскольку только в этом случае отсутствует и внешний (dq_e=0)и внутренний теплообмен (нет трения и dq_r=dl_r=0), общий приток тепла к жидкости dq=dq_e+dq_r=0 и, следовательно, dS=dq/T=0. Таким образом, характерным для изоэнтропийного торможения является то, что оно не сопровождается диссипацией энергии, т.е. необратимым процессом преобразования механической энергии в тепло. Происходит лишь «обратимое», т.е. «допускающее возврат к исходным параметрам» изменение соотношения в жидкости внешних или механических составляющих - потенциальной (p/r® p^*/r^*), кинетической (W²/2®0), и внутренней (u=C_vT® C_vT^*) составляющей полной энергии жидкости.

При изотермическом изоэнтропийном торможении, что, очевидно, может иметь место только в случае энергоизолированного течения идеальной несжимаемой жидкости, будет происходить изменение соотношения только внешних механических составляющих энергии жидкости, т.е. будет происходить лишь переход «кинетической энергии направленного движения» в «потенциальную энергию давления».

Состояние жидкости в точке торможения можно также охарактеризовать и соответствующими температуре торможения T^* величинами давления p^* и плотности r^*. При этом следует особо подчеркнуть, что все упомянутые выше

параметры торможения - a^*, T^*, p^*, r^*, являются константами для каждого заданного энергоизолированного течения идеальной жидкости, т.е., другими словами, они постоянны для всех точек изоэнтропийного течения.

Особую роль играет температура торможенияT^*, которую принято называть также ещё и «полной температурой»,поскольку она однозначно определяет полную удельную энергию жидкости - 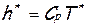. Последняя, напомним, представляет собой сумму потенциальной (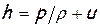) и кинетической (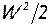) составляющих энергии и в энергоизолированном потоке сохраняет свое значение во всей области течения. Причем независимо от того, является ли течение «идеальным», при котором трения не существует по определению, или имеет место «реальный» необратимый процесс течения с сопутствующими ему «потерями энергии» на преодоление сопротивления сил трения, возникающих в вязкой жидкости. Это объясняется тем, что энергия, расходуемая движущейся жидкостью на преодоление любых сопротивлений, полностью превращается в тепло, которое воспринимается самой же жидкостью, т.е. «расходуемая энергия» в итоге всё равно остается в потоке, претерпевая только необратимое превращение в тепло. Таким образом, преодоление сопротивления сил трения вязкой жидкостью не может изменить полной энергии жидкости, а лишь вызывает необратимое качественное превращение её внешней механической (кинетической - 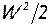) энергии во внутреннюю тепловую (потенциальную - u) энергию. Только в таком контексте можно говорить о «потерях энергии», связанных с трением в жидкости: происходит лишь потеря «механической энергии направленного движения», точнее необратимый переход её в «тепловую энергию покоя», а не потеря энергии вообще. Не надо забывать, что мы рассматриваем энергоизолированное течение и, стало быть, по определению, энергия «теряться», т.е. передаваться за пределы рассматриваемой системы не может!

Полная температура определяется соотношением

,

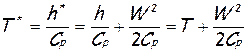где в общем случае все параметры – h^*, h, T^*, T и W, относятся к одному и тому же сечению элементарной струйки. Однако в расчетной практике наибольшее распространение получили производные от приведенного здесь соотношения формулы, представляющие отношение полной и термодинамической температуры в потоке сжимаемой жидкости как функцию той или иной безразмерной скорости (обычно - числа Маха, приведенной λ или относительной Λ скорости).

Вторым, после температуры торможения, важнейшим параметром является давление торможения p^*, которое, по аналогии с температурой торможения T^*, обычно называют «полным давлением», поскольку в изоэнтропийном потоке этот параметр также однозначно определяет полную энергию жидкости. В отличие от температуры торможения T^*, которая, так же как и энтальпия – h^*, имеет вполне определённое значение, постоянное вдоль любого энергоизолированного потока, полное давление p^* и плотность r^* в общем случае могут принимать любые значения в зависимости от характера течения («характера процесса»), но их отношение p^*/r^* тем не менее должно оставаться постоянным. Для изоэнтропийного процесса связь между давлением и плотностью устанавливается уравнением изоэнтропы .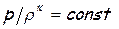

Используя уравнение изоэнтропы, выразим плотность жидкости r через давление в потоке p

;

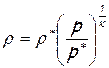отношение давления к плотности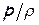

;

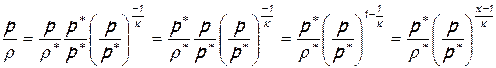и из уравнения энергии для элементарной струйки «на участке торможения»:

,

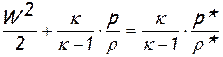получим соотношение, однозначно связывающее основные газодинамические параметры движущейся жидкости – давление p и скорость W, с параметрами изоэнтропийного торможения:

.

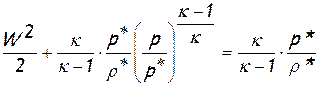Последнее уравнение обычно называют интегральным уравнением Бернулли или «интегралом» Бернулли для сжимаемой жидкости, поскольку оно может быть получено в результате интегрирования вдоль элементарной струйки (линии тока) непосредственно дифференциального уравнения движения идеальной жидкости. В отличие от приведенного выше уравнения энергии, которое связывает три параметра (скорость, давление и плотность), интеграл Бернулли связывает два параметра (скорость и давление), но справедлив только для изоэнтропийного течения. Напомним, что уравнение энергии составлено для энергоизолированной элементарной струйки и справедливо также и для неизоэнтропийных течений.

В случае несжимаемой жидкости (r=const) интеграл Бернулли принимает особенно простой вид:

,

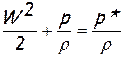откуда могут быть получены простые соотношения, выражающие связь между полным давлением p^*, термодинамическим или статическим давлениемp и скоростью W в сечении элементарной струйки несжимаемой жидкости:

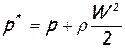или ,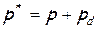

где 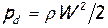- так называемое «динамическое давление» или «динамический напор» жидкости. Таким образом, полное давление p^*, определяемое полную энергию несжимаемой жидкости, складывается из «потенциальной» части этой энергии - статического давления в жидкости p, и «кинетической» составляющей энергии жидкости – динамического давления p_d . Напомним, что здесь рассматривалась исключительно невесомая жидкость!

Поскольку полученное количественное соотношение между давлением, скоростью и параметрами торможения сжимаемой жидкости в форме интеграла Бернулли достаточно громоздко (содержит дробную степень!), то его непосредственное использование в расчетной практике и преобразование, с целью получения явных зависимостей в общем виде, зачастую представляют значительные трудности. Проблема существенно упрощается в случае использования так называемых «газодинамических функций» и «изоэнтропических формул», устанавливающих связь между действительными параметрами и параметрами изоэнтропийного торможения в зависимости от безразмерных скоростей течения жидкости - числа Маха, приведенной λ или относительной Λ (число Чаплыгина)скорости.

Поясним понятие параметров торможения с помощью тепловой h-S диаграммы (см. рис.22). Пусть точка 1 соответствует статическим или термодинамическим параметрам – h, p, T, жидкости, движущейся со скоростью W. Тогда, если полностью затормозить эту жидкость (W=0) без необратимых потерь энергии, т.е. изоэнтропийно (dS=0), то параметрам торможения – h^*, p^*, T^*, полученным в результате осуществления такого идеального процесса, на тепловой диаграмме можно будет поставить в соответствие некоторую точку 0. Очевидно, что положение этой точки можно определить, отложив от точки 1 вверх отрезок, пропорциональный величине W²/2. Температуру T^* и давление p^* изоэнтропийного торможения (температуру и давление в точке 0) можно определить расчетным путем: по уравнению энергии – температуру, а давление - из уравнения изоэнтропы.

Любой реальный процесс торможения жидкости происходит с необратимыми потерями энергии, т.е. неизоэнтропийно (dS>0). Величина потерь в том или ином случае может быть ничтожно малой, но в любом реальном процессе эти потери есть.

Такой реальный процесс может быть условно изображен на тепловой диаграмме линией 1 – 2. При этом точки 0 и 2 будут принадлежать одной и той же линии постоянной энтальпии («изоэнтальпе»), поскольку из уравнения энергии следует, что величина полной энтальпии (полной энергии) жидкости в энергоизолированном процессе её торможения не зависит от того, как происходит торможение – с потерями или без. В конце концов, вся кинетическая энергия, в том числе и «потерянная», все равно переходит во внутреннюю тепловую энергию жидкости, так как теплообмена с внешней средой нет. Температура торможения также не зависит от характера процесса торможения жидкости, если она (жидкость) термодинамически совершенна. Но, как видно из рисунка, давление торможения в точке 2 несколько меньше аналогичного параметра в точке 0: p₂^*< p₀^*, т.е. величина давления торможения зависит от характера процесса торможения. В энергетически изолированных течениях (h^*=const) «гидравлические сопротивления» приводят к увеличению энтропии и снижению полного давления.

В заключении следует особо подчеркнуть, что при определении параметров торможения не обязательно имеется в виду реальное торможение потока. Также не обязательно приписывать им смысл параметров жидкости в некоторой конкретной точке торможения, которой в общем случае в рассматриваемом потоке может и не быть.

Параметры торможения следует понимать как расчетные параметры, которые мы получили бы, если бы смогли полностью затормозить рассматриваемый поток жидкости без необратимыхпреобразований механической энергии.

Параметры торможения можно формально вычислить в любой точке потока по соответствующим формулам. Так, например, параметры изоэнтропийного торможения можно вычислить в данной точке потока, хотя само течение может и не быть изоэнтропийным. Вместе с тем важно отметить, что параметры изоэнтропийного торможения являются физическими понятиями, т.е. соответствующие параметры могут быть измерены, хотя, конечно, с определенной погрешностью, так как при измерении нельзя полностью исключить теплообмен. Измерение параметров изоэнтропийного торможения имеет большое значение при проведении газодинамических экспериментов.