
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Распространение волн малых возмущений (звуковых волн) в дозвуковом, звуковом и сверхзвуковом потоках
|
|
Движение жидкости со скоростями, превышающими скорость звука, существенно отличается от дозвукового движения. Наиболее заметно эти особенности проявляются в характере распространения звуковых волн в жидкости.
В неподвижном газе слабые возмущения распространяются во все стороны в виде продольных волн давления сферической формы, в центре которых находится источник возмущения. Поскольку звук передается посредством таких волн, они называются звуковыми. В потоке газа распространение слабых возмущений происходит несколько иначе, в связи с тем, что источник возмущений непрерывно перемещается относительно той среды, в которой распространяются волны. Поскольку это связано с относительным движением, то совершенно безразлично, перемещается ли обтекаемое тело в неподвижной среде или на неподвижный объект набегает поток газа.
На рисунке 53 изображены четыре схемы распространения волн: одна — в неподвижном газе и три — в движущемся с дозвуковой, звуковой и сверхзвуковой скоростью.
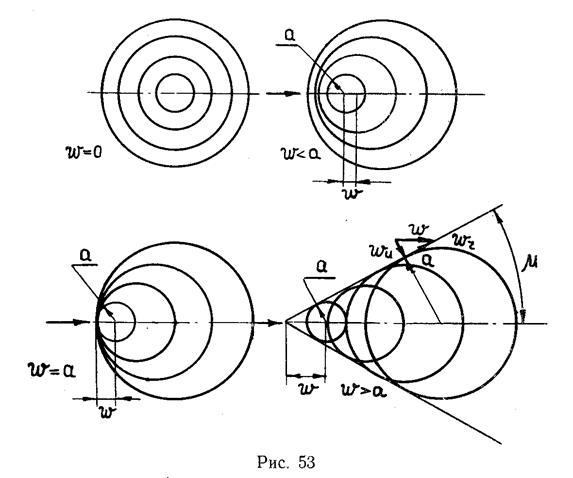
Если w < а, то возмущения распространяются во все стороны, в том числе и вверх по течению. Правда, вниз по течению абсолютная скорость распространения волн получается больше, так как скорость волны складывается со скоростью течения газа.
При обтекании различных тел несжимаемой жидкостью или дозвуковым потоком газа жидкость, как показывают наблюдения, начинает огибать препятствие, еще находясь впереди него на некотором расстоянии. Это отклонение потока вызвано теми возмущениями (волнами давления), которые от носка обтекаемого тела распространяются вверх по течению.
Если скорость потока равна скорости распространения звука w = а, то центр каждой образовавшейся волны плывет вниз по течению с той же скоростью, с которой волна перемещается относительно газа. Поэтому возмущения распространяются только вниз по течению и вбок, но не проникают выше того места, где образуются волны, а, достигнув его, концентрируются там. Это место называют иногда звуковым барьером, придавая данному названию смысл некоторой преграды, не пропускающей слабые возмущения вверх по течению [1]. При w > а слабые волны, скорость которых равна звуковой, сносятся вниз по течению сверхзвуковым потоком, поэтому возмущенная зона ограничена некоторым конусом, за пределами которого поток остается невозмущенным. Этот конус называется конусом слабых возмущений, конусом влияния или конусом Маха. Образующие конуса носят название линий слабых возмущений или линий Маха. В плоском потоке вместо конуса рассматривается угол малых возмущений или угол Маха.
Рассматривая угол слабых возмущений на рисунке 53, можно сделать такие выводы:
1) синус угла слабых возмущений равен отношению скорости звука к скорости потока, что следует непосредственно из чертежа; иначе говоря,
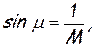 (4.68)
(4.68)
2) составляющая скорости набегающего потока, перпендикулярная линии слабых возмущений, равна местной скорости распространения звука
wu = а, (4.69)
так как только в этом случае линии слабых возмущений будут занимать устойчивое положение, не расходясь и не сближаясь.
Линии слабых возмущений существуют только в сверхзвуковом потоке. Дифференциальное уравнение потенциала скорости для этого потока решается методом характеристик. Характеристиками дифференциального уравнения являются линии, имеющие вполне определенный физический смысл. Это такие линии, проведенные в потоке, у которых касательные в каждой точке совпадают по направлению с линиями слабых возмущений в этих же точках. В общем случае характеристики криволинейны, но могут быть и такие течения, в которых они прямолинейны и, следовательно, полностью совпадают с линиями слабых возмущений. В этом частном случае характеристики и линии слабых возмущений отождествляют.
& [2] Глава 4 §6[3] с.36…40. [5] с.?…?.
& [6] с.183…184. [7] с.119…120. [8] с.?…?.
Date: 2015-09-03; view: 1722; Нарушение авторских прав