Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Расчет спектра собственных колебаний по уточненной схеме
|
|
Для начала сосредоточим массы стержней в их средних и крайних точках, причем средней точке каждого стержня придадим половину его массы, а крайним – по ¼ этой величины. Обозначим эти массы согласно рисунку 5.
Рисунок 6 – Расположение и обозначение сосредоточенных масс
Подсчитаем величину каждой массы mi и занесем значения в таблицу 1.
Таблица 1 – Значения сосредоточенных масс
| Номер массы | Величина, кг |
| 1529+8,798=1537,798 | |
| 17,595 | |
| 8,798*2+17,595=35,19 | |
| 17,595 | |
| 8,798+17,595=26,393 | |
| 35,19 | |
| 35,19 | |
| 17,595 | |
| 17,595 | |
| ∑ | 1740,141 |
Выполним проверку. Как видно из рисунка 5, суммарная длина всех стержней рамы составляет 6L. Тогда масса всей рамы вместе с электродвигателем составит
,
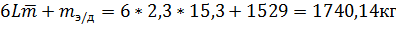что согласуется с таблицей 1.
Пронумеруем динамические степени свободы системы с сосредоточенными массам, и, учитывая наложенные связи, направим соответствующим образом оси обобщенных координат (см. рисунок 6).
Рисунок 7 – Направления осей обобщенных координат
Матрица масс для такой системы (при данной нумерации сосредоточенных масс и динамических степеней свободы) будет иметь вид:
Построим эпюры изгибающих моментов от единичных сил, приложенных к соответствующим сосредоточенным массам по направлениям обобщенных координат (рисунки 7, 8, 9).
Рисунок 8 – Единичные эпюры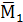 
, 
, 
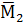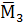
Рисунок 9 – Единичные эпюры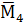 
, 
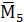
Рисунок 10 – Единичные эпюры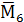 
, 
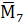
Коэффициенты податливости системы δij определим на ЭВМ.
Проконтролируем результаты расчетов сравнением некоторых di,j, вычисленных вручную и на ЭВМ, а также используя свойство взаимности коэффициентов di,j = dj,i. Например, в результате ручного расчета получено значение коэффициента d11 = d0 
= 3,999×10-6 м/Н. Расчет на ЭВМ дает значение коэффициента 4×10-6 м/Н. Разница объясняется учетом влияния продольных деформаций стержней в машинном расчете, а также погрешностями округления. Ниже в таблице 1 приведены значения коэффициентов в ручном и машинном расчетах (необходимо делать анализ размерностей).
Таблица 1
| Ручной расчет | Расчет на ЭВМ | |
| d11 | 3,999×10-6 | 4×10-6 |
| d22 | 0,665×10-6 | 0,666×10-6 |
| d21 | -0,331×10-6 | -0,333×10-6 |
получим следующий вид матрицы относительной податливости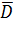 
(обозначена ниже как D1):
Матрицу C определим выражением
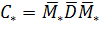(4.1),
где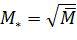 
, и вычислим ее собственные числа λ. Первые три собственных числа: λ1=3,317*105, λ2=4,747*104, λ3=3,353*103. Частоты собственных колебаний найдем так:
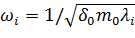(4.2).
Результаты расчетов: ω1=6,272 с-1, ω2=16,58 с-1, ω3=62,383 с-1. Первые две частоты незначительно отличаются от найденных в п. 3.2 в меньшую сторону вследствие учета масс стержней.
Собственные формы колебаний определим по формуле
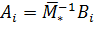(4.3),
где Bi – собственные векторы матрицы С. В данном случае собственные формы примут вид:
С помощью данных векторов построим первые три формы собственных колебаний рамы (рисунок 10).
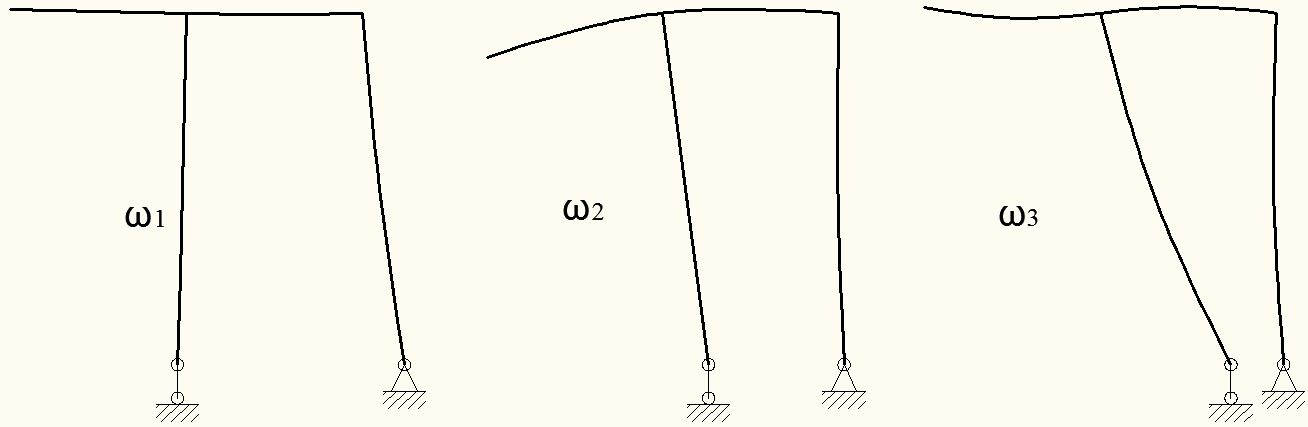
Рисунок 11 – Первые три формы собственных колебаний рамы
Date: 2015-09-03; view: 371; Нарушение авторских прав