
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Краткая теория
|
|
Манипулятор - это кинематическая цепь, образованная последовательным или последовательно-параллельным соединением тел, называемых кинематическими звеньями, и предназначенная для преобразования движения этих звеньев в требуемое (заданное) движение схвата. При этом кинематические звенья соединяются друг с другом подвижно с помощью кинематических пар.
Кинематическая цепь, образующая манипулятор, имеет два оконечных звена: одно из них будет являться основанием - стойкой (ему присваивается нулевой номер), а другое оконечное звено оснащается схватом. Этому оконечному звену присваивается последний п-й номер, равный при последовательном соединении звеньев числу подвижных звеньев манипулятора.
Кинематическое звено - совокупность жестко соединенных друг с другом тел, входящих в состав механизма, в данном случае в состав манипулятора.
Кинематическая пара - подвижное соединение двух кинематических звеньев, допускающее их вполне определенное движение относительно друг друга.
Элементы кинематической пары - поверхности, линии или точки, по которым соприкасаются звенья, образующие данную кинематическую пару.
Кинематическая цепь - это совокупность кинематических звеньев, подвижно соединенных друг с другом с помощью кинематических пар.
Если в кинематической цепи есть кинематические звенья, входящие в одну кинематическую пару, то такая цепь называется разомкнутой, а если же каждое звено входит как минимум в две кинематических пары, то это замкнутая кинематическая цепь.
Манипулятор может быть образован как на основе разомкнутой кинематической цепи (рис. 1а) с последовательным соединением звеньев (антропоморфные человекоподобные роботы) и на основе замкнутой кинематической цепи (рис. 1б) с последовательно-параллельным соединением звеньев (роботы с параллельной кинематикой, в частности, гексаподы на основе платформы Стюарта). Итак, манипулятор - это механизм, представляющий собой разомкнутую или замкнутую кинематическую цепь, предназначенную для получения требуемого движения схвата в пространстве.

а) б)
Рис. 1. Манипулятор а) на основе разомкнутой цепи б) с параллельной кинематикой
Для обеспечения пространственного движения схвата в общем случае достаточно трех переносных степеней подвижности робота, расположенных относительно друг друга определенным образом. Основными минимальными (необходимыми) условиями обеспечения пространственного движения схвата в манипуляторе, образованного парами 5-го класса, являются:
1. наличие двух вращательных пар с непараллельными осями (обычно оси в этом случае перпендикулярны друг другу) и третьей вращательной или поступательной пары, обеспечивающей изменение радиуса сферы (рис. 2а);
2. наличие двух вращательных пар с параллельными осями и третьей поступательной пары, направляющая которой неперпендикулярна осям вращательных пар, или вращательной пары, ось которой непараллельна осям предыдущих пар (рис. 2б);
3. наличие двух поступательных пар с непараллельными направляющими и одной вращательной пары (рис. 2в), ось которой неперпендикулярна плоскости, образованной осями направляющих поступательных пар, или поступательной пары, направляющая которой непараллельна названной плоскости (обычно направляющие перпендикулярны друг другу, а ось вращательной пары параллельна плоскости).
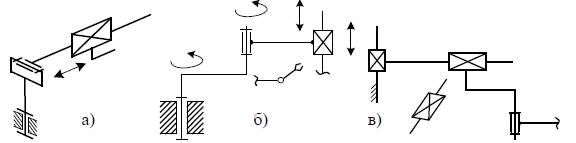
Рис. 2. Переносные движения манипулятора
Переносные степени подвижности удобно классифицировать по системам координат, которую обеспечивает та или иная комбинация кинематических пар манипулятора.
Различают четыре основные системы координат манипуляторов:
1.
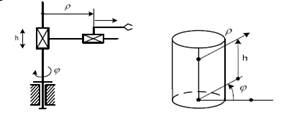 |
Цилиндрическая;
2. Сферическая;
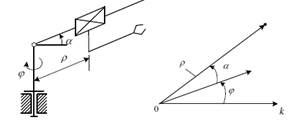 |
3.
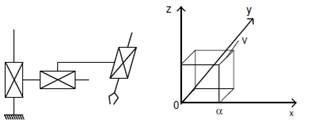 |
Прямоугольная;
4. Ангулярная (угловая).

Если в заданной точке рабочего пространства манипулятора его схват должен иметь вполне определенную ориентацию, то манипулятор необходимо снабдить тремя ориентирующими степенями подвижности. Хотя в промышленных роботах обычно обходятся одной - двумя ориентирующими степенями подвижности.
Чтобы не вносить помехи в положение схвата или свести их к минимуму, ориентирующие степени подвижности делают так, чтобы они как можно меньше перемещали схват.
Правила расположения осей и начал координат специальной системы координат относительно кинематических пар и звеньев манипулятора.
Пронумеруем кинематические звенья A от неподвижного звена до наиболее удаленного, на котором закреплен схват, присвоив им соответственно номера от 0 до n (рис. 3), где n - число подвижных звеньев манипулятора.
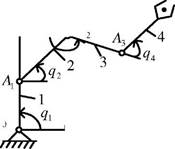
Рис. 3. Нумерация кинематических звеньев
Обозначим кинематические пары символом Аь нижний индекс которого равен меньшему из номеров звеньев, образующих кинематическую пару.
Например, кинематическая пара А1 соединяет кинематические звенья 1 и 2, а кинематическая пара А3 - кинематические звенья 3, 4 и т. д.
Введем понятие оси Zj i-й кинематической пары. Осью Zj i-й вращательной кинематической пары, соединяющей i-ое звено с ^+1)-м является ось шарнира кинематической пары. Эту ось будем считать принадлежащей i-му звену и жестко с ним соединенной. Именно вокруг этой оси вращается ^+1)-е звено относительно i-го.
Осью Zi поступательной пары является какая-либо из прямых, параллельная направляющей данной поступательной пары. Если ось zi не параллельна оси zi-1, то ее рекомендуется направлять так, чтобы она пересекалась с этой осью.
За положительное направление оси zi можно взять любое, в частности, направление снизу вверх, слева направо, в направление к наблюдателю или близкие к ним направления. Важным моментом при расположении системы координат на i-м звене манипулятора является выбор ее начала координат Oi и направление оси xi.
Однородные координаты. Матрица перехода 4x4 кинематической пары.
При составлении математических моделей манипуляторов наибольшее распространение получило матричное исчисление (матричное исчисление было предложено в 1857г. английским ученым Кэли). Долгое время для этой цели использовалось сочетание матриц поворота размером 3x3, элементами которых были направляющие косинусы углов между осями (трех осей одной системы координат относительно трех осей другой), и матриц переноса размером 3x1, элементами которых служили координаты по трем осям начала соответствующей системы координат.
Наличие двух матриц разной размерности и разного назначения привело к необходимости использовать операции умножения и сложения матриц, к усложнению алгоритма вычисления, а следовательно, к увеличению машинного времени, что сказывается на отработке управляющих сигналов в реальном времени и на управляемости робота.
В последние десятилетия стали использовать комплексные матрицы перехода размером 4x4, позволяющие осуществлять поворот и перенос (смещение) одних координат по отношению к другим. В этом случае для описания положения точки в пространстве используются однородные координаты, в которых к обычным координата добавляется четвертая, равная единице, то есть координатами точки будут (xj, yj zj, 1). Если известны однородные координаты (xj, yj, zj, 1) вектора rj некоторой точки Aj в "старой" i-ой системе координат, то однородные координаты (xj-1, yj-1, zj-1, 1) вектора rj-1 этой точки Aj в "новой" системе координат рассчитываются в общем случае по формулам:

В общем случае, чтобы совместить «новое» положение со «старым» i-м положением системы, используя движение «новой» системы к «старой», необходимо шесть независимых перемещений относительно трех осей координат.
Однако при использовании специальных систем координат и так называемых преобразований Денавита-Хартенберга достаточно четырех перемещений, осуществленных в следующей последовательности (рис. 4):
Поворот системы (i-1) вокруг оси Zi-1 против часовой стрелки (если смотреть со стороны оси Zi-1) на угол 0. до тех пор, пока ось Xi-1 не станет параллельной и однонаправленной с осью Xj;
Сдвиг повернутой (ь1)-й системы вдоль оси Zi-1 на величину Si до тех пор, когда ось Xi-1 совпадет с осью Xi;
Сдвиг системы (i-1) вдоль оси Xi на величину ai до совпадения начал координат систем (i-1) и i;
Поворот (ь1)-й системы вокруг оси Xi против часовой стрелки (если смотреть со стороны оси Xi) на угол а до совмещения оси Zi-1 с осью Zi.
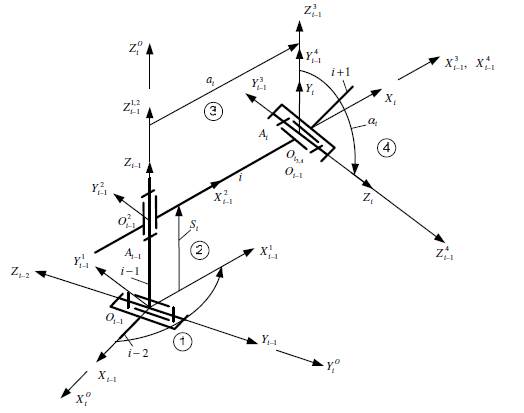
Рис. 4. Преобразований Денавита-Хартенберга
Прямая задача кинематики манипуляторов заключается в определении положения его звеньев в неподвижной (инерциальной) системе координат по известным значениям обобщенных координат и при известных значениях кинематических размеров звеньев.
Важным частным видом прямой задачи кинематики манипулятора является определение положения его схвата, закрепленного на последнем n-м звене манипулятора.
Положение схвата в неподвижной системе координат будет определено полностью, если будут известны координаты его центра Ап и ориентация последнего n-го звена в неподвижной системе координат.
Date: 2015-09-03; view: 949; Нарушение авторских прав