Техническое задание. Дана массивная стальная плоская рама с установленным на ней электродвигателем весом Q=15 кН (рисунок 1)

Дана массивная стальная плоская рама с установленным на ней электродвигателем весом Q=15 кН (рисунок 1). Поперечные сечения всех стержней рамы одинаковы и выполнены в виде составного сечения из двух швеллеров. Вследствие вращения неуравновешенного ротора электродвигателя со скоростью n=214 об/мин возникает центробежная сила величиной Р=2,1 кН, которая вызывает колебания рамы.

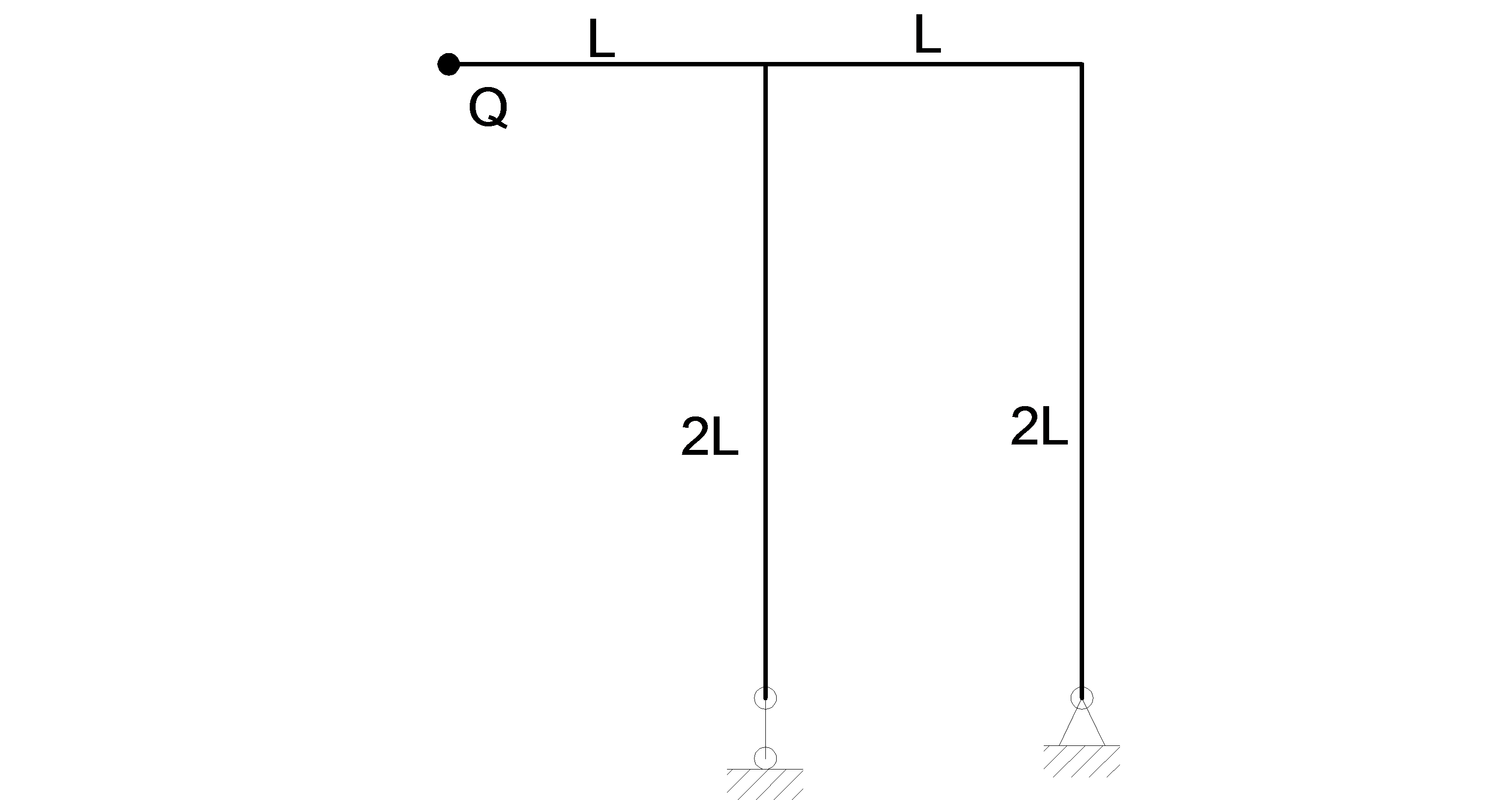
Рисунок 1 – Исследуемая плоская рама

Требуется:

1) подобрать номер швеллера из условия статической прочности;

2) используя упрощенную расчетную схему с двумя степенями свободы, определить собственные частоты колебаний ω₁ и ω₂, формы колебаний, пренебрегая массой стержней рамы;

3) рассчитать спектр собственных колебаний рамы по уточненной схеме, приближенно учитывающей массу стержней рамы;

4) рассматривая стационарный режим колебаний, определить амплитуду установившихся колебаний массы электродвигателя и рассчитать траекторию движения центра масс электродвигателя;

5) построить эпюру амплитудных значений изгибающих моментов, возникающих в раме от действия заданной вибрационной нагрузки при стационарном режиме колебаний;

6) вычислить максимальные динамические напряжения в сечениях рамы (с учетом собственного веса двигателя) и сравнить их с расчетным сопротивлением материала;

7) сравнить значения максимальных динамических напряжений со значениями, полученными из статического расчета и сделать заключение о прочности рамы.

Расчетное сопротивление стали изгибу принять равным R_u= 210 МПа, модуль упругости стали Е = 200 ГПа, длина L=2,3 м.

Динамический расчёт плоской рамы.

Дано: l = 6м,Q = 40кН, F = 4кН,

№ схемы = 6,h =2,5 м, EI = 21000 кНм²;

Задание для плоской рамы:

1) Определить круговую частоту вынужденных колебаний θ, равной 0,9 минимальной частоты собственных колебаний системы;

2) Выполнить расчёт на динамическое воздействие вибрационной нагрузки Fsin(θt);

Решение

1) Определение минимальной частоты собственных колебаний рамы.

Построение эпюр изгибающих моментов в основной системе метода сил от y₁ = 1.

Каноническое уравнение имеет вид:

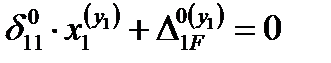
Главный коэффициент – собственные перемещения d₁₁ – находим «перемножением» эпюры 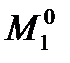самой на себя.

Используем правило и Верещагина, и Симпсона:

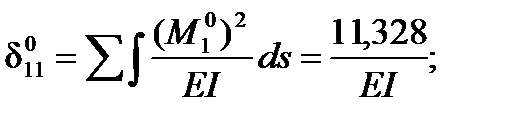
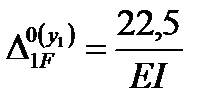
Решая уравнение,

получаем:

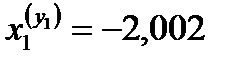
строим эпюру

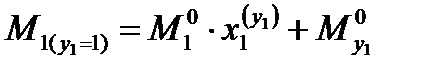
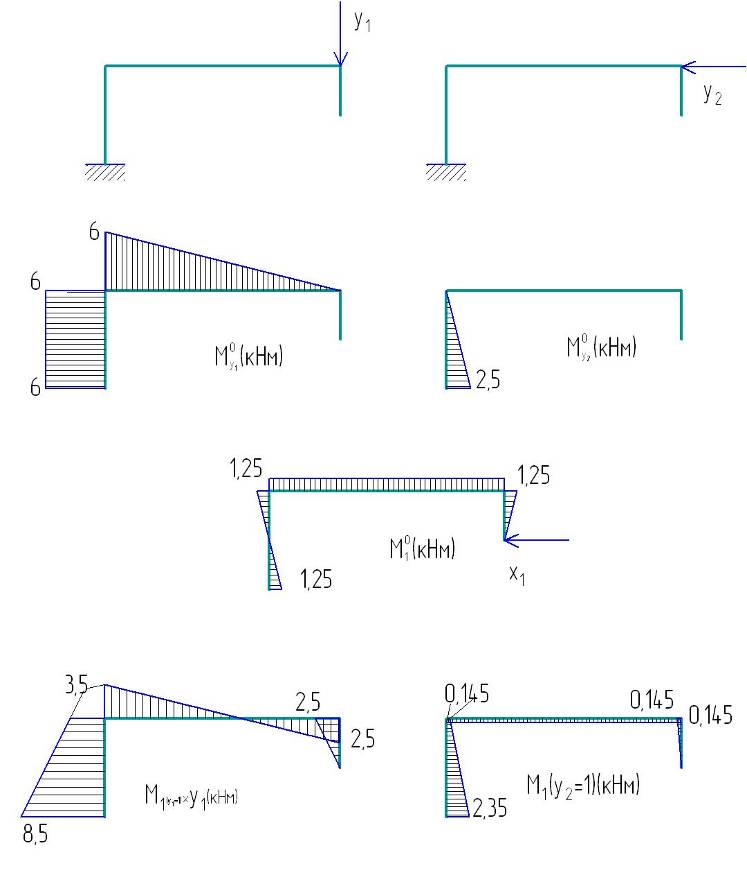
Построение эпюр изгибающих моментов в основной системе метода сил от y₂ = 1.

Каноническое уравнение имеет вид:

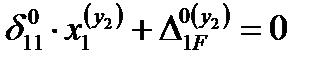
Главный коэффициент – собственные перемещения d₁₁ – находим «перемножением» эпюры 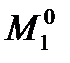самой на себя.

Используем правило и Верещагина, и Симпсона:

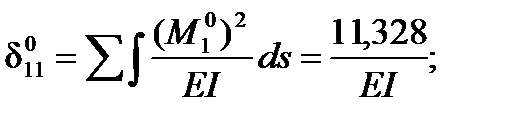
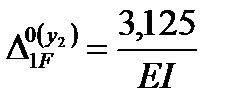
Решая уравнение,

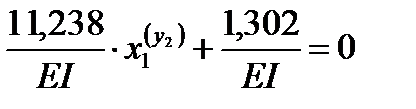
получаем:

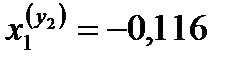
строим эпюру

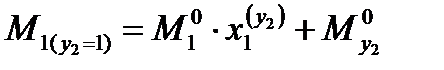
Система уравнений свободных колебаний:

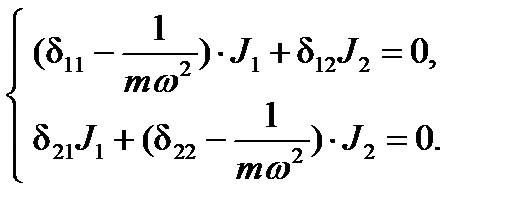
Определяем коэффициенты:

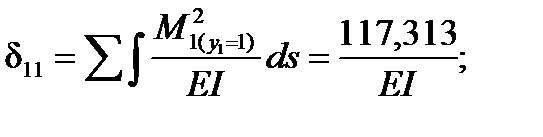
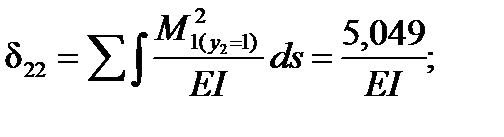
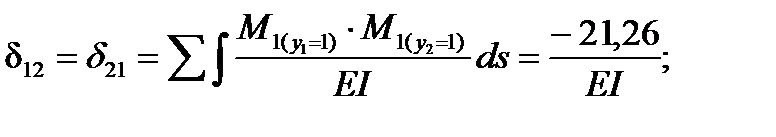
Умножаем оба уравнения на EI:

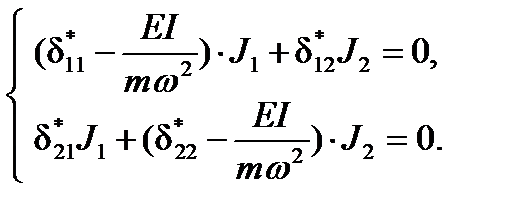
Величину 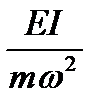обозначаем через λ.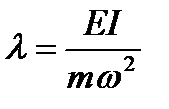

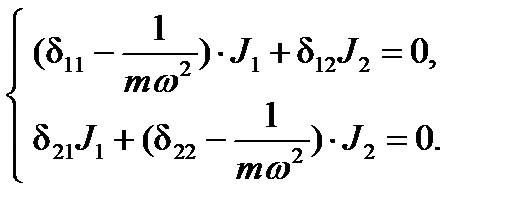
Условие существования ненулевого решения имеет вид:

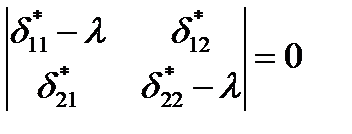
Раскрывая определитель, получаем квадратное уравнение относительно λ:

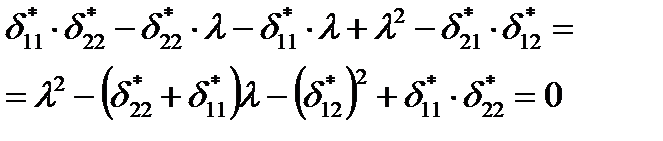
Подставляя численные значения коэффициентов, решаем уравнение:

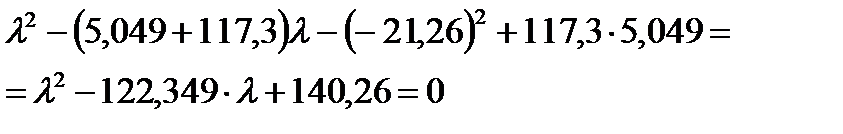
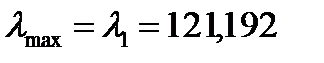
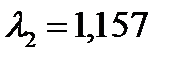
Вычисляем минимальную круговую частоту собственных колебаний рамы:

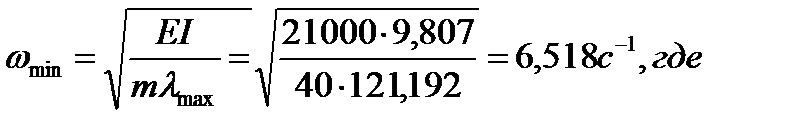
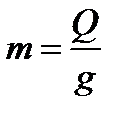
Date: 2015-09-03; view: 471; Нарушение авторских прав