
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Ход работы
|
|
Данные для выполнения лабораторной работы приведены в таблице 1.
Таблица 1. Данные работы
| Условное обозначение структурной схемы | |||
| манипулятора | Система координат | ||
| мнемоническое | цифровое | ||
| В, П||,В^x,В^+0 | 1, 8, 4, 7 | Цилиндрическая | |
Используемые кинематические пары:
1. Вращательная кинематическая пара, образованная стойкой манипулятора и его первым подвижным звеном.
2. Поступательная кинематическая пара, ось которой параллельна оси Z предыдущей кинематической пары.
3. Вращательная кинематическая пара, ось которой перпендикулярна оси Z предыдущей кинематической пары и перекрещивается с этой осью.
4. Вращательная кинематическая пара, ось которой перпендикулярна оси Z предыдущей кинематической пары, пересекается с ней и обеспечивает ротационное движение звена.
Манипулятор используем с четырьмя степенями подвижности (тремя переносными и одной ориентирующей).
Кинематические размеры манипулятора назначаем в миллиметрах и градусах так, чтобы схват не удалялся от некоторой центральной вертикальной оси, связанной со стойкой манипулятора, ориентировочно более чем на 1000 мм.
При назначении кинематических размеров манипулятора указываем кратчайшие расстояния между осями кинематических пар, длины направляющих, пределы изменения обобщенных координат, углы между осями звеньев и осями кинематических пар, т.е. те линейные и угловые размеры звеньев манипулятора, которые определяют взаимное расположение его звеньев и пар и в конечном итоге положение и ориентацию каждого промежуточного звена манипулятора и его схвата относительно неподвижной инерциальной системы координат.
Обозначим кинематические пары символом Ai, нижний индекс которого равен меньшему из номеров звеньев, образующих кинематическую пару.
Описание систем координат:
Система O0X0Y0Z0 выбрана произвольно при обеспечении направления оси Z0 по оси кинематической пары А0.
В системе O1X1Y1Z1 ось Z1 направлена по оси кинематической пары A1 повернута на угол 225 градусов относительно оси предыдущей кинематической пары. начало координат в точке пересечения осей, ось Х1 направлена перпендикулярно осям Z0 и Z1 Направление оси У1 выбрано так чтобы обеспечить правую систему координат.
В системе O2X2Y2Z2 ось Z2 направлена по направляющей кинематической пары A2 которая перекрещивается с осью предыдущей кинематической пары.Ось X2 перпендикулярна осям Z1 и Z2, направление оси У2 выбрано так чтобы обеспечить правую систему координат.
В системе O3X3Y3Z3 ось Z3 направлена по оси кинематической пары A3 перпендикулярно оси предыдущей кинематической пары. Начало координат в точке пересечения осей, ось X3 направлена перпендикулярно осям Z2 и Z3, направление оси У2 выбрано так чтобы обеспечить правую систему координат.
Чтобы определить значения названных параметров для заданной или спроектированной кинематической схемы манипулятора, мысленно совмещаем систему координат Оц Xj-1 Yj-1 Zj-1 с системой координат Oj Xj Yj Zj.
0j - это угол, на который надо повернуть систему (i-1) вокруг оси Zj-1 против часовой стрелки (если смотреть со стороны оси Zj-1) чтобы ось Xj-1 стала параллельной и однонаправленной с осью Xj.
Sj - расстояние на которое нужно переместить (i-1)-ую систему вдоль оси Zj-1 до совпадения оси Xj-1 с осью Xj.
aj - расстояние на которое нужно переместить (i-1)-ую систему вдоль оси Xj до совпадения начал координат систем (j-1) и j;
αj - угол, на который необходимо повернуть (i-1)-ую систему вокруг оси Xj против часовой стрелки (если смотреть со стороны оси Xj) до совмещения оси Zj-1 с осью Zj.
Обобщенная координата - qj.
Схема изображена на рис. 5.
Таблица кинематических пар – таблица 2.
Таблица 2. Таблица кинематических пар
| номер (i-1) кинематической пары | тип (i-1) кинематической пары | номер i-го подвижного звена | параметры кинематической пары | |||
| θi (Qi) | Si | ai | αi | |||
| Вращательная | q1 | |||||
| Поступательная | q2 | |||||
| Вращательная | q3 | |||||
| Вращательная | q4 |
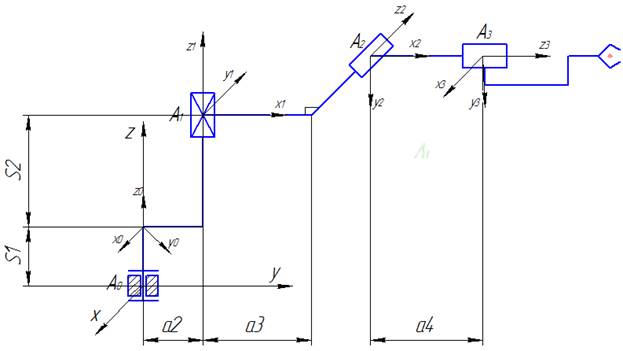
Рис. 5. Схема манипулятора
Зададим исходные значения в программе MathCAD.
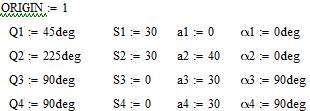
Матрицы перехода для кинематических пар:

Расчет матриц перехода для каждой кинематической пары с выделением из них необходимых значений координат и углов ориентации:
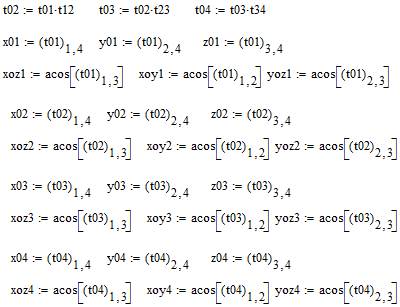
Объединим итоговые данные:
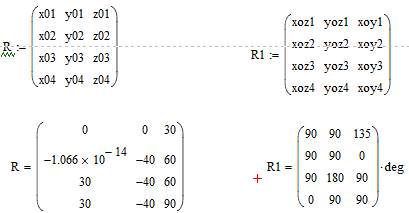
В матрице R содержатся координаты кинематических пар, а в матрице R1 направляющие углы.
При изменении начальных данных, результат будет пересчитываться автоматически.
Построим модель манипулятора в программе FRONT. Модель манипулятора – рис.6. Исходные данные для расчета – (Рис.7)Диаграммы абсолютные – рис.8, диаграммы обобщенные – рис. 9.
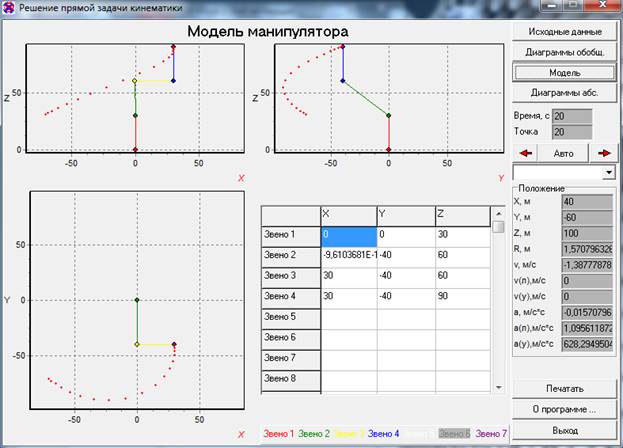
Рис. 6. Модель манипулятора
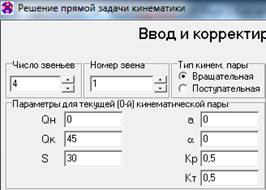
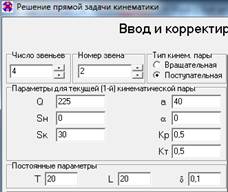


Рис.7 Данные для расчета

Рис. 8. Диаграммы абсолютные

Рис. 9. Диаграммы обобщенные
Заключение
В данной работе разработана кинематическая схема манипулятора и математическая модель кинематики манипулятора. Решена первая задача в программе MathCAD. Произведено построение модели, проверка результата решения первой задачи. Задача решена правильно.
Список литературы
1. Механика промышленных роботов. Кн. 1: Кинематика и динамика / Е.И. Воробьев, С. А. Попов, Г.И. Шевелева.-М.: Высш. школа, 1988.-304с.
2. Шахинпур М. Курс робототехники: Пер. с англ.-М.: Мир, 1990.-527с.
3. Фу К., Гонсалес Р., Ли К., Робототехника: Пер. с англ.-М.: Мир, 1989.-624с.
4. Хомченко В.Г. Решение прямой и обратной задач кинематики манипуляторов промышленных роботов: Омск, ОмГТУ, 1995.-26с.
Date: 2015-09-03; view: 908; Нарушение авторских прав