Метод кинетостатики (Принцип Даламбера)

Для решения задач динамики несвободной материальной точки удобным является метод кинетостатики. Содержание этого метода заключается в следующем. Записываем основное уравнение (3.1) динамики точки в виде

.

Введя обозначение , получаем

. (3.47)

Вектор 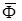, равный по модулю произведению массы точки на ее ускорение и направленный противоположно вектору ускорения, называется силой инерции.

Равенство (3.47) представляет собой уравнение движения материальной точки, записанное в форме условия равновесия сил. В этом и заключается существо метода кинетостатики.

Метод кинетостатики является формальным приемом сведения уравнения динамики к форме уравнения статики.

Реакция связи, в соответствии с уравнением (3.47), равна

.

Для решения конкретных задач векторное уравнение (3.47) необходимо спроецировать на соответствующие оси координат, в частности, на оси декартовой системы координат:

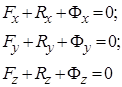(3.48)

и на оси естественного трехгранника:

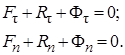(3.49)

Так же как и для одной материальной точки, дифференциальным уравнениям движения материальной системы можно придать форму уравнений статики. Этот метод часто применяется в инженерных расчетах, особенно при определении динамических реакций опор твердого тела.

Рассматриваем материальную систему, состоящую из n материальных точек.

Для каждой точки запишем основное уравнение динамики –

, (k = 1,2, ..., n)

и придадим вид уравнений статики

, (3.50)

где сила инерции .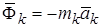

Складывая почленно все уравнения (3.50), получим

.

Первая сумма 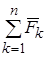равна главному вектору 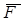всех активных сил, приложенных к системе.

Вторая сумма - главному вектору 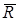реакций связей.

Третья сумма 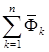- главному вектору 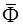сил инерции.

Учитывая это, записываем уравнение кинетостатики

, (3.51)

которое можно прочитать следующим образом:

В каждый момент времени движения материальной системы сумма главных векторов активных сил, реакций связей и сил инерции равна нулю.

Выберем произвольный неподвижный центр О, и положение каждой точки 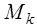определим с помощью радиуса вектора 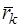. Умножая каждое из уравнений (3.50) векторно слева на соответствующий 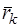и складывая почленно все произведения, получаем

.

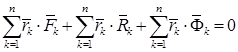Первая сумма равна главному моменту 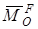всех активных сил, приложенных к системе, вторая сумма – главному моменту всех реакций связей системы, а последняя – главному моменту 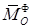сил инерции. Следовательно, имеем

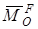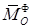+ + =0, (3.52)

то есть в каждый момент времени движения материальной системы сумма главных моментов активных сил, реакций связей и сил инерции равна нулю.

При решении конкретных задач от двух векторных уравнений (3.51), (3.52) – переходят к шести уравнениям в проекциях на оси декартовых координат:

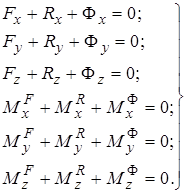(3.53)

За оси координат можно выбрать любую систему декартовых осей, как неподвижных, так и перемещающихся произвольным образом в пространстве, но только каждый раз следует правильно определять проекции главного вектора и главного момента 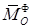сил инерции.

Движение твердого тела полностью определяется этими шестью уравнениями кинетостатики, так же как равновесие твердого тела вполне определяется аналогичными шестью уравнениями, за исключением проекций главного вектора сил инерции и проекций главного момента сил инерции .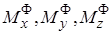

Если рассматриваемая система состоит из нескольких тел, то уравнения кинетостатики можно составить для всей системы и для каждого тела в отдельности.

Пример. Тело массой m может скользить по поверхности призмы, имеющей угол наклона (рис. 3.15). С каким ускорением 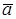должна двигаться призма по горизонтальной поверхности, чтобы тело относительно призмы оставалось неподвижным? Трение скольжения между телом и призмой отсутствует.

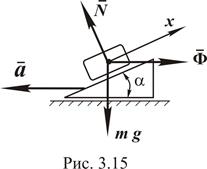
Решение. Изображаем действующие на тело силы: - сила тяжести, - нормальная реакция и - сила инерции, которая по модулю равна произведению массы тела на ускорение движения, то есть 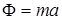и направлена в противоположную сторону вектора ускорения .

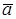С телом связываем ось x, направленную перпендикулярно реакции 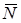, так как по условию реакцию N находить не требуется.

Проецируем все силы на ось x:

,

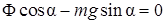то есть записываем уравнение кинетостатики, откуда находим силу инерции

и затем ускорение призмы

,

.

Видим, что ускорение должно быть тем больше, чем больше угол 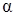. При 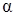, стремящемся к 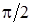, ускорение стремится к бесконечности.

Пример. Центр тяжести С махового колеса смещен относительно его оси вращения на величину 1 мм. Ось вращения вала горизонтальна (рис. 3.16). Масса колеса m = 300 г, колесо находится на валу посередине, между подшипниками, и вращается равномерно, делая n = 1200 об/мин.

Найти статические и добавочные динамические реакции подшипников.

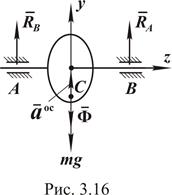
Решение. Вначале определим статические реакции подшипников, направленные перпендикулярно оси вала, обозначив их 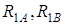. Проецируем все силы на ось y:

.

Здесь сила инерции не учитывается. Поскольку маховик находится в середине, между подшипниками, то статические реакции равны между собой и их значения определяются так:

.

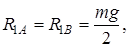
Для определения добавочных динамических реакций воспользуемся методом кинетостатики, введя силу инерции 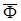маховика. Так как маховик вращается равномерно, то центр тяжести С имеет только осестремительное (нормальное) ускорение , направленное к оси вала и равное .

Здесь - угловая скорость вращения маховика; ОС - смещение центра тяжести маховика относительно оси вращения.

Следовательно, сила инерции маховика направлена в противоположную сторону ускорения 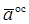, поэтому ее еще называют центробежной силой инерции. По модулю она равна

.

Определяем угловую скорость

,

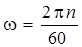или

.

Записываем уравнение кинетостатики в проекции на ось y

.

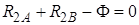Здесь сила тяжести не учитывалась.

Находим добавочные динамические реакции:

;

;

.

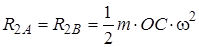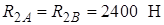Сравнивая статические и добавочные динамические реакции, видим, что последние в 1,6 раза больше первых. К тому же следует заметить, что динамические реакции пропорциональны квадрату угловой скорости, то есть при ее повышении они будут возрастать по квадратичному закону.

Date: 2015-09-03; view: 1387; Нарушение авторских прав