
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Моменты инерции тел простейшей геометрической формы
|
|
Моментом инерции материальной точки относительно некоторой оси называется произведение массы m этой точки на квадрат ее расстояния h до оси:
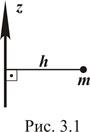
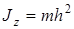 . (3.8)
. (3.8)
Моментом инерции материальной системы относительно оси называется сумма моментов инерции всех точек системы относительно тойже оси:
 . (3.9)
. (3.9)
При непрерывном распределении массы сумма переходит в интеграл.
Момент инерции относительно оси представляет определенно положительную величину. Размерность момента инерции в системе СИ равна 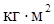 .
.
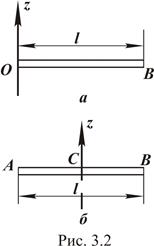 Момент инерции однородного тонкого стержня массы М и длины l относительно оси z, проходящей перпендикулярно стержню через его конец (рис. 3.2, а), равен
Момент инерции однородного тонкого стержня массы М и длины l относительно оси z, проходящей перпендикулярно стержню через его конец (рис. 3.2, а), равен
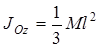 (3.10)
(3.10)
и относительно оси, проходящей через его центр тяжести (рис. 3.2, б), равен
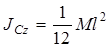 . (3.11)
. (3.11)
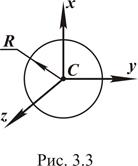
Момент инерции материального круга смассой М и радиусом R относительно оси z, перпендикулярной плоскости круга и проходящей через его центр тяжести (см. рис. 3.3), равен
 . (3.12)
. (3.12)
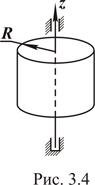
Момент инерции однородного круглого цилиндра (рис. 3.4) относительно продольной оси z равен
 , (3.13)
, (3.13)
где М - масса цилиндра; R - радиус.
Моменты инерции относительно параллельных осей. Существует простая связь между моментами инерции тела относительно параллельных осей, одна из которых проходит через центр масс, а именно момент инерции тела относительно некоторой оси равен сумме момента инерции тела относительно оси, проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояния между осями.
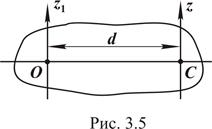
Пусть 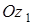 - ось, относительно которой определяется момент инерции тела (рис. 3.5), а
- ось, относительно которой определяется момент инерции тела (рис. 3.5), а 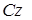 - ось, проходящая через центр масс тела, параллельно первой. Тогда
- ось, проходящая через центр масс тела, параллельно первой. Тогда
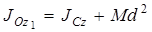 , (3.14)
, (3.14)
где d - расстояние между осями.
Пример. Определим момент инерции материального круга относительно оси, перпендикулярной плоскости круга и проходящей через точку, находящуюся на расстоянии R от его центра (см. рис. 3.6):

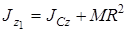 ,
,
так как
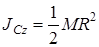 , то
, то
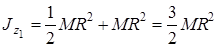 .
.
Date: 2015-09-03; view: 1484; Нарушение авторских прав