Работа силы. Мощность

В курсе физики понятие работы вводится следующим образом. Пусть материальная точка М движется по прямой линии ВС и на нее действует сила 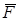, постоянная по модулю и направлению (рис. 3.7).

Угол между силой и скоростью точки обозначим через 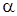. Тогда работа постоянной силы 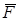на прямолинейном перемещении точки 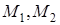определяется как произведение модуля силы на величину перемещения 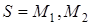и на косинус угла между ними, то есть

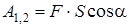. (3.15)

Это же равенство можно записать в виде скалярного произведения:

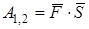, (3.16)

где - вектор перемещения точки.

В системе СИ единицей измерения работы является Джоуль, 1 Дж = 1 Нм.

Формулы (3.9) и (3.10) справедливы в случае действия постоянной силы как по модулю, так и по направлению, а также тогда, когда точка движется только прямолинейно. В случае переменной силы и криволинейной траектории движения точки определяется вначале элементарная работа

, (3.17)

где dS - дифференциал перемещения точки. Так как дифференциал перемещения dS равен модулю дифференциала радиуса-вектора 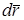, то есть dS = dr, то элементарную работу можно записать как

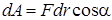
или через скалярное произведение

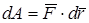, (3.18)

а также через проекции векторов

. (3.19)

Мощность N силы 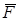определяется как скорость изменения работы:

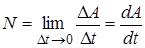, (3.20)

или

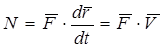, (3.21)

то есть мощность N равна скалярному произведению силы 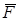на скорость точки. Единицей измерения мощности в системе CИ является Ватт, 1 Вт = 1 Дж/с.

3.6. Работа сил,
приложенных к материальной точке и твёрдому телу

Работа силы тяжести. Пусть точка М, на которую действует сила тяжести, перемещается из положения в положение (рис. 3.8).

Проекции силы на оси координат равны 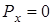, , 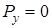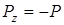. Используя выражение (3.19), определяем

.

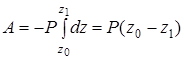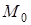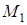Если точка выше , то 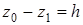, где h величина вертикального перемещения точки; если же точка 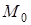ниже точки 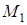, то .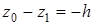

Поэтому можно записать

. (3.22)

Следовательно, работа силы тяжести равна произведению модуля силы на вертикальное перемещение точки её приложения, взятое с соответствующим знаком. Если точка перемещается вверх, то знак минус, если вниз, - то плюс.

Работа силы тяжести не зависит от вида траектории перемещения точки.

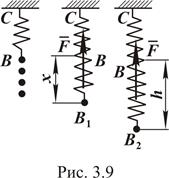Работа силы упругости. Рассмотрим пружину ВС, конец C которой закреплён неподвижно (рис. 3.9). При растяжении пружины возникают силы упругости, и на тело, вызывающее растяжение, действует реакция пружины 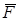. Эта сила направлена противоположно перемещению свободного конца пружины, а её модуль пропорционален удлинению пружины:

,

где с - коэффициент жесткости пружины.

Ось x направим по оси пружины, приняв за начало координат конец недеформированной пружины В. Проекция силы 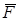на ось х определяется как

.

Вычислим работу силы упругости на перемещении, используя понятие элементарной работы (3.19):

.

Проекции силы упругости на оси:

;

;

,

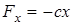отсюда элементарная работа силы упругости

,

а работа силы упругости на перемещении 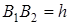определяется как

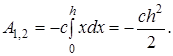(3.23)

Работа силы упругости отрицательна в том случае, когда деформация увеличивается, то есть когда сила упругости направлена противоположно перемещению её точки приложения, и положительна, когда деформация уменьшается.

Работа силы, приложенной к вращающемуся телу. Пусть сила 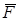приложена в некоторой точке тела, отстоящей от оси вращения z на величину h (см. рис. 3.10).

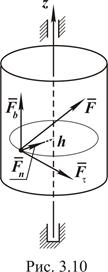Точка приложения силы описывает при своём движении окружность радиуса h. Разложим силу 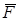по осям естественного трёхгранника и обозначим её составляющие через 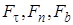. Работа составляющих 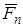и равна нулю, так как эти силы перпендикулярны к перемещению точки их приложения. Следовательно, работа силы равна работе eё касательной составляющей.

Для элементарной работы имеем

,

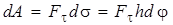где 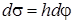- дифференциал дуговой координаты точки приложения силы, а 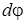- дифференциал угла поворота тела. Учитывая, что произведение 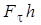равно моменту силы относительно оси вращения тела, получаем

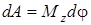. (3.24)

Элементарная работа силы, приложенной к вращающемуся телу, равна моменту этой силы относительно оси вращения, умноженному на дифференциал угла поворота тела. Работа силы 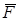на конечном углу поворота определяется как

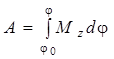, (3.25)

где 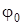и 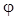- начальное и конечное значение угла поворота тела.

Если момент является постоянной величиной, то есть 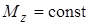, то

. (3.26)

Делим обе части равенства (3.24) на и получаем выражение для мощности силы, приложенной к вращающемуся телу:

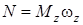, . (3.27)

Мощность силы 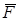, приложенной к вращающемуся телу, равна произведению момента 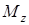этой силы относительно оси вращения на угловую скорость тела.

3.7. Теорема об изменении кинетической энергии
материальной точки

Определим связь между работой сил, приложенных к материальной точке, и изменением её скорости движения. Для этого воспользуемся основным уравнением динамики точки

,

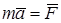или

,

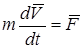где 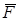- равнодействующая всех сил, приложенных к материальной точке. Умножим скалярно обе части этого выражения на дифференциал радиуса-вектора :

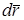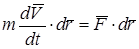. (3.28)

Видно, что правая часть является элементарной работой dA сил, действующих на точку. Левую часть можно представить в виде

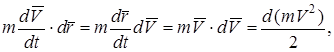
при этом учтено, что 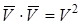. С учётом этого равенство (3.28) записывается в форме

. (3.29)

В левой части

(3.30)

есть кинетическая энергия материальной точки. С учётом (3.24) выражение (3.29) принимает вид

(3.31)

и представляет собой математическую запись теоремы об изменении кинетической энергии точки в дифференциальной форме: полный дифференциал кинетической энергии материальной точки равен элементарной работе всех действующих на эту точку сил.

Разделив обе части равенства (3.31) на dt, получаем

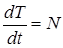, (3.32)

так как

.

Таким образом, полная производная по времени от кинетической энергии материальной точки равна мощности всех действующих на точку сил.

Пусть материальная точка М перемещается по кривой ВС (см. рис. 3.11) от положения 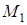до положения 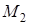. Обозначим через 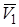и скорость точки в положениях 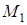и 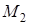соответственно и проинтегрируем обе части равенства (3.29):

.

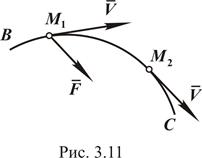
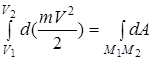Правая часть этого равенства равна работе 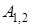силы на перемещении 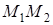. Таким образом, после интегрирования и подстановки пределов имеем

, (3.33)

то есть изменение кинетической энергии материальной точки, при переходе её из начального положения в конечное, равно работе силы, приложенной к точке. Это есть интегральная форма теоремы.

Date: 2015-09-03; view: 954; Нарушение авторских прав