Кинетическая энергия материальной системы

Как было установлено, кинетическая энергия материальной точки определяется как

,

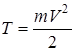то есть половина произведения массы m точки на квадрат её скорости.

Кинетической энергией материальной системы называется сумма кинетических энергий всех точек, входящих в систему, таким образом,

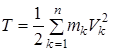. (3.34)

Здесь скорости 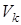определяются относительно неподвижной системы координат, то есть это абсолютные скорости. Из кинематики сложного движения точки известно, что абсолютное движение можно представить состоящим из переносного и относительного движений. Такой подход довольно часто позволяет упростить вычисление кинетической энергии системы.

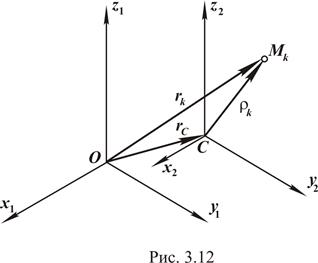
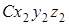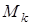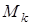Итак, движение системы рассматриваем относительно неподвижных осей (см. рис. 3.12). Вводим подвижные координатные оси , перемещающиеся поступательно относительно неподвижных осей, причём начало координат совпадает с центром масс. Пусть - одна из точек материальной системы массы . Положение точки относительно неподвижной системы координат определяется радиусом-вектором 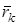, а относительно подвижной - радиусом-вектором .

На основании теоремы о сложении скоростей абсолютная скорость точки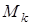

, (3.35)

где 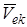- переносная скорость; 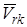- относительная скорость.

Так как подвижная система координат 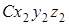совершает поступательное движение, то переносные скорости всех точек одинаковы и равны скорости , отсюда

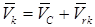, (3.36)

подставив (3.36) в выражение кинетической энергии (3.34), имеем

.

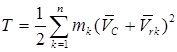Возведём скобку в квадрат и разобьём сумму на три части:

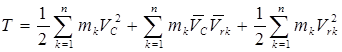. (3.37)

Здесь учтено, что скалярный квадрат любого вектора равен квадрату его модуля, то есть

;

.

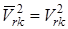Последнее слагаемое – - есть кинетическая энергия относительного движения.

В первом слагаемом множитель 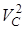не зависит от индекса суммирования и его можно вынести за знак суммы, то есть

.

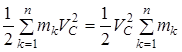Сумма есть масса М всей системы, отсюда

,

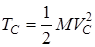что представляет собой кинетическую энергию центра масс системы.

Рассматриваем второе слагаемое выражения (3.37). Выносим 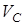за знак суммы, имеем

.

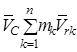Это выражение равно нулю, так как

.

Определяем относительный радиус-вектор центра масс

,

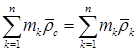где - относительный радиус-вектор, определяющий положение точки с номером k относительно начала подвижной системы координат.

В связи с тем, что центр С масс системы совпадает с началом подвижной системы координат 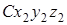, 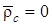и, соответственно,

.

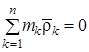Дифференцируя по времени, получаем

.

Таким образом, выражение (3.37) для кинетической энергии принимает вид

. (3.38)

Кинетическая энергия материальной системы в ее абсолютном движении складывается из кинетической энергии (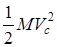) центра масс, в предположении, что в нем сосредоточена масса всей системы, и кинетической энергии 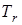системы в ее относительном движении.

Date: 2015-09-03; view: 706; Нарушение авторских прав