
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Кинетическая энергия твердого тела
|
|
Так как твердое тело рассматривается как непрерывно распределенная масса, то все суммы, входящие в выражения для кинетической энергии материальной системы, переходят в интегралы, а масса 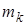 отдельной точки заменяется дифференциалом dm. Поэтому для твердого тела формула (3.32) принимает вид
отдельной точки заменяется дифференциалом dm. Поэтому для твердого тела формула (3.32) принимает вид
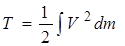 , (3.39)
, (3.39)
где интегрирование производится по всей массе тела.
Определим кинетическую энергию твердого тела при различных видах его движения.
Поступательное движение. При поступательном движении твердого тела скорости всех точек одинаковы. Поэтому в формуле (3.39) 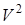 можно вынести за знак интеграла, то есть
можно вынести за знак интеграла, то есть
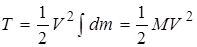 , (3.40)
, (3.40)
где 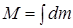 .
.
Таким образом, кинетическая энергия твердого тела, движущегося поступательно, равна половине произведения массы тела на квадрат его скорости.
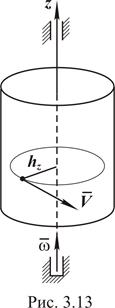
Вращательное движение. При вращательном движении твердого тела вокруг неподвижной оси (рис. 3.13) модуль скорости любой точки определяется по формуле
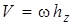 ,
,
где 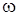 - модуль угловой скорости тела,
- модуль угловой скорости тела, 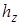 - кратчайшее расстояние от точки до оси вращения z.
- кратчайшее расстояние от точки до оси вращения z.
Подставляя в формулу (3.40) значение скорости V, получаем
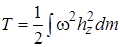 ,
,
или, вынося за знак интеграла 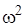 , так как угловая скорость для всех точек тела одинакова, имеем
, так как угловая скорость для всех точек тела одинакова, имеем
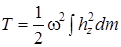 .
.
Интеграл 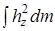 зависит только от характера распределения массы по объему тела и не зависит от кинематического состояния. Он называется моментом инерции тела относительно оси z и обозначается символом
зависит только от характера распределения массы по объему тела и не зависит от кинематического состояния. Он называется моментом инерции тела относительно оси z и обозначается символом 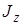 :
:
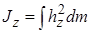 . (3.41)
. (3.41)
Следовательно,
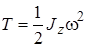 , (3.42)
, (3.42)
то есть кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.
Момент инерции тела представляет меру его инерции во вращательном движении.
Плоскопараллельное движение. При плоском движении твердого тела вектор угловой скорости 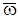 всегда перпендикулярен к плоскости движения. Для определения кинетической энергии тела воспользуемся формулой (3.38)
всегда перпендикулярен к плоскости движения. Для определения кинетической энергии тела воспользуемся формулой (3.38)
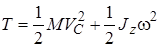 , (3.43)
, (3.43)
учитывая, что момент инерции 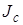 определяется относительно оси, проходящей через центр масс тела.
определяется относительно оси, проходящей через центр масс тела.
3.10. Теорема об изменении кинетической энергии
материальной системы
Установим взаимосвязь между изменением кинетической энергии материальной системы и работой приложенных сил.
Рассматриваем два момента времени: начальный 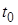 и текущий, или конечный,
и текущий, или конечный, 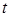 .
.
Пусть модуль скорости точки с индексом k в момент времени 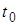 равняется
равняется 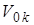 , а в момент времени t -
, а в момент времени t - 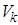 .
.
Записываем для каждой точки теорему об изменении кинетической энергии (3.33):
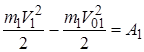 ,
,
………………………
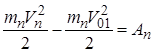 .
.
Складывая почленно все равенства, получаем
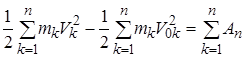 , (3.44)
, (3.44)
или, учитывая выражение для кинетической энергии системы (3.34), имеем
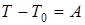 , (3.45)
, (3.45)
где 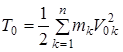 - начальное значение кинетической энергии;
- начальное значение кинетической энергии;
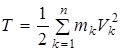 - конечное значение кинетической энергии;
- конечное значение кинетической энергии;
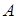 - работа всех внешних и внутренних сил системы.
- работа всех внешних и внутренних сил системы.
Равенство (3.45) представляет математическую запись теоремы об изменении кинетической энергии материальной системы в интегральной форме: изменение кинетической энергии материальной системы при переходе ее из начального в текущее (конечное) положение равно сумме работ на этом перемещении всех действующих на систему сил.
Продифференцируем равенство (3.45) по времени:
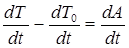 ;
;
так как 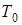 есть величина постоянная, то
есть величина постоянная, то
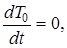
а 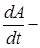 мощность сил, получим
мощность сил, получим
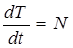 . (3.46)
. (3.46)
Это уравнение представляет математическую запись теоремы об изменении кинетической энергии в дифференциальной форме: производная кинетической энергии по времени равна сумме мощностей всех сил, приложенных к системе.
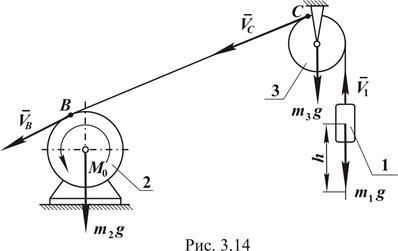
Пример. Груз 1 массой 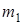 поднимается с помощью электрической лебедки (см. рис. 3.14). Барабан 2 приводится во вращение электромотором, который создает постоянный вращающий момент
поднимается с помощью электрической лебедки (см. рис. 3.14). Барабан 2 приводится во вращение электромотором, который создает постоянный вращающий момент 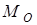 . Моменты инерции блока 3 и барабана 2 относительно их осей вращения равны соответственно
. Моменты инерции блока 3 и барабана 2 относительно их осей вращения равны соответственно 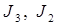 , а их радиусы - R и r. Определить угловую скорость вращения барабана 2 в тот момент, когда груз 1 поднимется на высоту h. В начальный момент система находилась в покое. Массой троса пренебречь.
, а их радиусы - R и r. Определить угловую скорость вращения барабана 2 в тот момент, когда груз 1 поднимется на высоту h. В начальный момент система находилась в покое. Массой троса пренебречь.
Решение. Применим теорему об изменении кинетической энергии материальной системы
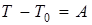 ,
,
и так как в начальный момент система находилась в покое, то
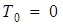 ,
,
поэтому имеем
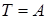 ,
,
где Т - кинетическая энергия системы в конечный момент времени, А - работа сил, действующих на систему. Определяем кинетическую энергию системы
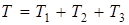 ,
,
где 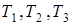 - кинетическая энергия груза, блока и барабана соответственно.
- кинетическая энергия груза, блока и барабана соответственно.
Барабан и блок вращаются вокруг неподвижных осей, поэтому согласно формуле (3.42)
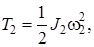
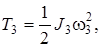
где 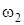 ,
, 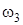 - угловые скорости барабана и блока. Скорость точки В касания троса с барабаном равна
- угловые скорости барабана и блока. Скорость точки В касания троса с барабаном равна 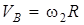 . Эту же скорость имеет и точка С касания троса с блоком, то есть
. Эту же скорость имеет и точка С касания троса с блоком, то есть 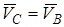 . Зная скорость
. Зная скорость 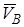 , находим угловую скорость блока
, находим угловую скорость блока
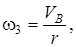
откуда
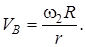
Следовательно,
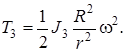
Груз 1 движется поступательно со скоростью
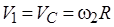 ,
,
так как трос нерастяжим.
Кинетическая энергия груза равна
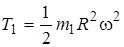 .
.
Подставляя выражения 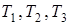 в выражение кинетической энергии системы, получаем
в выражение кинетической энергии системы, получаем
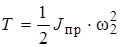 ,
,
где приведенный к оси вращения барабана момент инерции системы определяется равенством
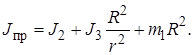
Перейдем теперь к определению работ. Работа сил тяжести барабана и блока, а также реакций их опор равна нулю, так как точки приложения этих сил неподвижны.
Работа силы тяжести груза равна
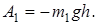
Работу вращающего момента 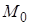 вычисляем по формуле (3.32)
вычисляем по формуле (3.32)
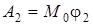 ,
,
где  - угол поворота барабана, равный
- угол поворота барабана, равный 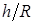 ; таким образом,
; таким образом,
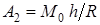 .
.
Работа всех сил, действующих на систему, равна
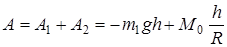 .
.
Подставляя значения Т и А в формулу Т = А, получаем
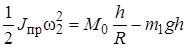 ,
,
откуда находим угловую скорость барабана
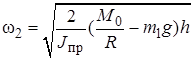 .
.
Date: 2015-09-03; view: 2749; Нарушение авторских прав