Предмет и задачи динамики. Законы динамики

ДИНАМИКА

Предмет и задачи динамики. Законы динамики

Предметом динамики является изучение движения материальных точек, тел и их систем с учётом действующих сил.

Все задачи динамики делятся на две.

Первая задача – закон движения точки задан, требуется найти силы, действующие на эту точку. Вторая задача обратная, силы являются заданными, а требуется найти закон движения.

Динамика построена на законах Ньютона.

Первый закон - изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения.

Фундаментальное значение для всей динамики имеет второй закон Ньютона: сила, действующая на материальную точку, сообщает ей ускорение, которое пропорционально величине силы и имеет направление силы. В аналитической форме этот закон представляется в виде

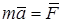, (3.1)

где 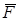- сила, действующая на материальную точку; 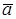- её ускорение; m - масса точки, являющаяся мерой её инертных свойств.

Третий закон Ньютона: две материальные точки взаимодействуют друг с другом так, что силы их взаимодействия равны по величине, противоположны по направлению и имеют общую линию действия.

Единица силы называется Ньютоном, из выражения (3.1) следует, что 1 Н = 1 кг×м/c .

3.2. Дифференциальные уравнения движения
материальной точки

Выражение (3.1) является основным уравнением динамики точки. Положение материальной точки определим радиус-вектором 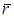. Сила, действующая на точку, может быть функцией радиус-вектора 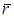, скорости 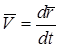(например, сила сопротивления) и времени t.

Следовательно, в общем случае основное уравнение динамики точки (3.1) можно записать в форме

. (3.2)

Это есть дифференциальное уравнение движения материальной точки в векторной форме. Спроецируем обе части уравнения (3.2) на неподвижные оси декартовых координат, получаем три уравнения:

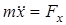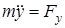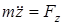, , , (3.3)

где 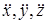- проекции ускорения точки на оси координат,

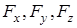- проекции силы на те же оси.

При проецировании уравнения (3.2) на оси естественного трехгранника получается

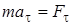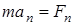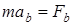, , , (3.4)

где - проекции силы на касательную, нормаль и бинормаль. Из кинематики известно, что

.

С учетом этого уравнения (3.4) принимают вид

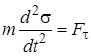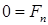, , . (3.5)

Date: 2015-09-03; view: 2557; Нарушение авторских прав