Полнота в смысле Фреше

Определение 1. Последовательность точек 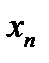эвклидова пространства сходится по норме к точке 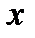, если числовая последовательность 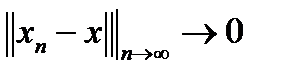, то есть 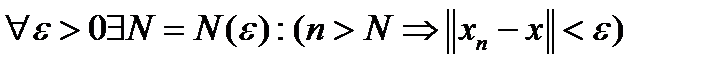. Обозначение используется обычное: .

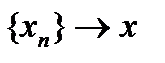Определение 2. Пусть множество M есть подмножество множества Е. Точка 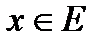называется предельной точкой множества M, если существует последовательность точек множества M, с попарно различными элементами, сходящаяся к x.

Комментарий. Чтобы точка 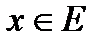была предельнойточкой множества M, надо каким 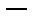либо образом исключить стационарные последовательности 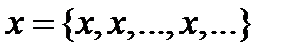, чтобы изолированные точки множества , то есть точки, у которых существует окрестность, не содержащая точек из множества , не могли оказаться предельными. В этом определении представлен один из таких вариантов.

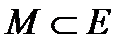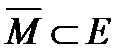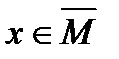Определение 3. Пусть множество . Множество называется замыканием множества , если для любой точки существует последовательность не обязательно различных точек из множества , сходящихся к точке х.

Определение 4. Множество называется замкнутым, если оно совпадает со своим замыканием то есть .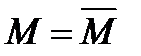

Комментарий. В определении допускаются стационарные, начиная с некоторого номера, последовательности. Поэтому любая изолированная точка множества замкнута. Позже мы рассмотрим этот вопрос подробнее.

Определение 5. Последовательность точек x_n эвклидова пространства 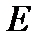называется фундаментальной, если .

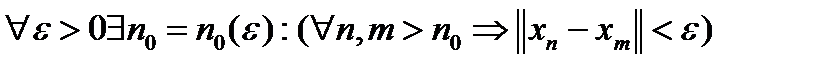Определение 5^*. Последовательность точек x_n эвклидова пространства 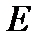называется фундаментальной, если .

Теорема 1. Последовательность точек 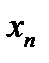эвклидова пространства фундаментальна, если она сходится по норме к точке .

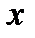Пусть 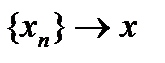. Тогда 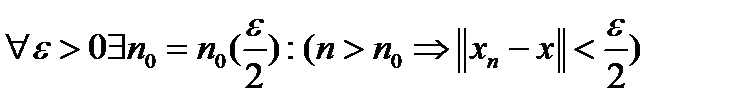. Выберем произвольные 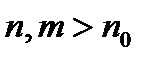. Тогда из неравенства треугольника .

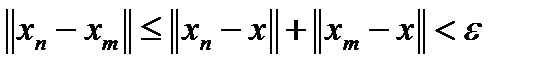Комментарий. Обратное, вообще говоря, неверно. Рассмотрим примеры.

Примеры. 1. Рассмотрим в пространстве всех интегрируемых по Риману функций 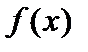на сегменте 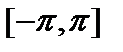подпространство, состоящее из всех многочленов. Пусть 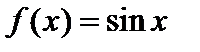. Согласно формуле Тейлора с остаточным членом в форме Лагранжа можем записать 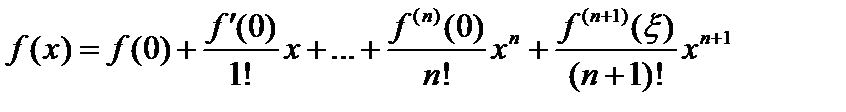, где 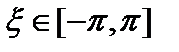.Обозначим через P_n (x) сумму первых n +1 членов в правой части этой формулы. Тогда P_n (x) есть многочлен степени n, причем 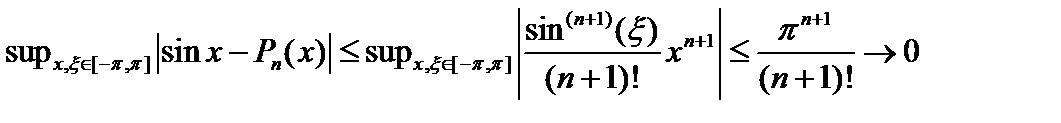при 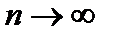.То есть последовательность P_n лежит в подпространстве многочленов, сходится к функции 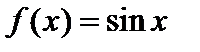, но предельная функция не лежит в пространстве многочленов 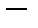синуса среди многочленов нет… Следовательно, рассматриваемое подпространство незамкнуто, хотя последовательность P_n (x) фундаментальна (хотя бы потому, что сходится). Причина в том, что мы из пространства выбросили часть функций, так что в оставшейся части образовались ”дырки”, одной из которых и является синус.

2. Такой же пример даёт множество рациональных чисел, рассматриваемое как подмножество числовой оси 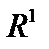. Последовательность Бернулли 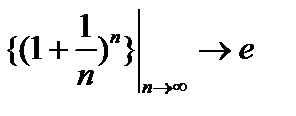, но числа 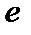среди рациональных чисел нет.

Определение 6. Эвклидово пространство 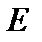называется полным (в смысле Фреше), если всякая его фундаментальная последовательность сходится.

Определение 9. Полное бесконечномерное эвклидово пространство называется гильбертовым.

Комментарий. Понятие полноты и в том и в другом случае, по сути, означает, что элементов, будь то пространства, или последовательности векторов, или еще чего-нибудь, должно быть достаточным для того, чтобы некоторое свойство выполнялось.

Date: 2015-09-03; view: 439; Нарушение авторских прав