Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Геометрия эвклидовых пространств
|
|
Теорема 1. (Неравенство Буняковского 
Коши или неравенство Шварца): 
.
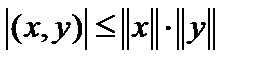. 1. Действительный случай. Пусть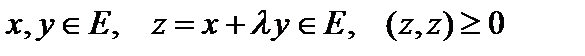 
, то есть 
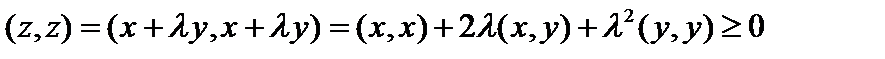. Это квадратное неравенство относительно 
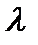выполнено 
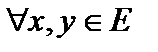если его дискриминант 
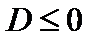, то есть 
.
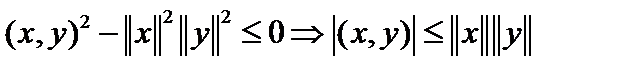2. Комплексный случай.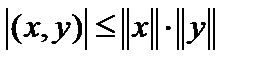 
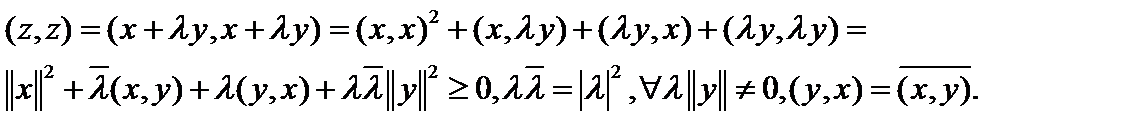Пусть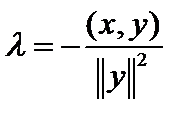 
. Подставив его в неравенство, получим 
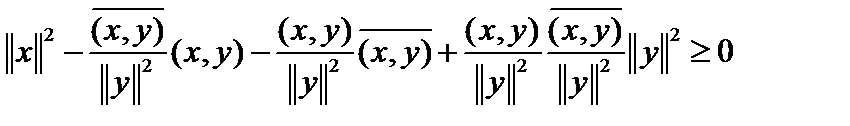, то есть 
.
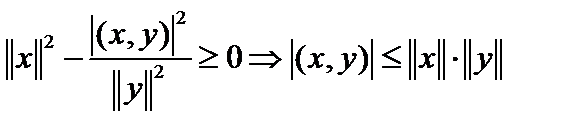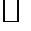
Теорема 2. (Неравенство Минковского или неравенство треугольника):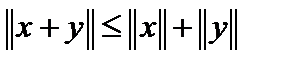 
.
. 
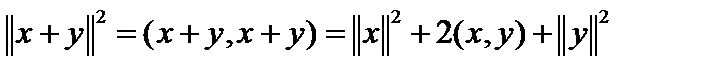, но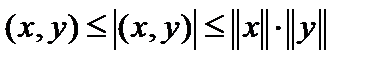 
. Тогда 
.
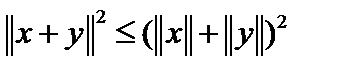Определение 2. Пусть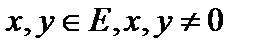 
. Углом между элементам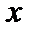и 
и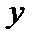 
называют число 
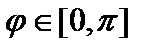, для которого выполняется равенство 
.
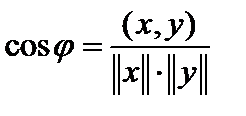Определение 3. Два элемента произвольного евклидова пространства называются ортогональными, если скалярное произведение этих элементов равно нулю.
Ясно, что 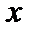и 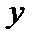ортогональны если и только если 
.
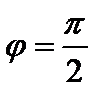Теорема 3. (Равенство параллелограмма):
.
. 
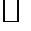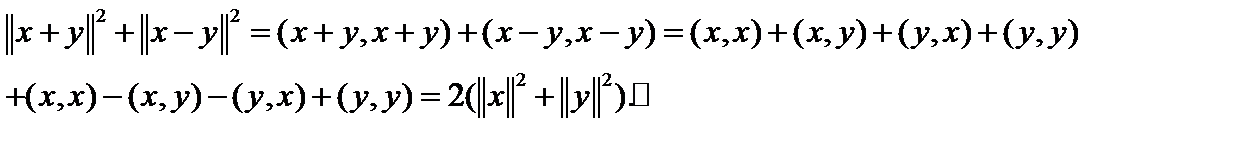
Следствие: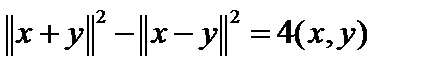 
.
Комментарий. В параллелограмме, построенном на векторах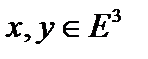 
, где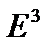 
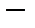обычное геометрическое пространство, диагонали задаются векторам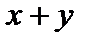и 
и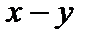 
, а как учат в восьмом классе, сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. Равенство параллелограмма является бесконечномерным обобщением этого факта. При неэвклидовых нормах равенство параллелограмма не выполняется.
Пример. В линейном пространстве последовательностей комплексных чисел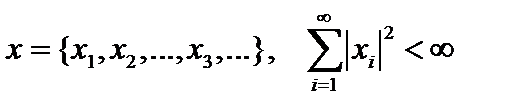 
, скалярное произведение 
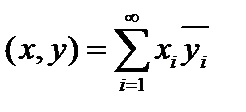. Аксиомы скалярного произведения очевидны. Ряды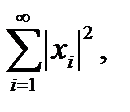 
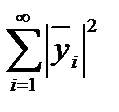сходятся по условию, а из неравенства Буняковского–Коши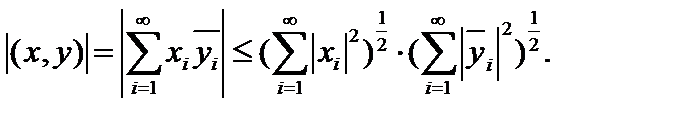 
Date: 2015-09-03; view: 429; Нарушение авторских прав