Линейная структура

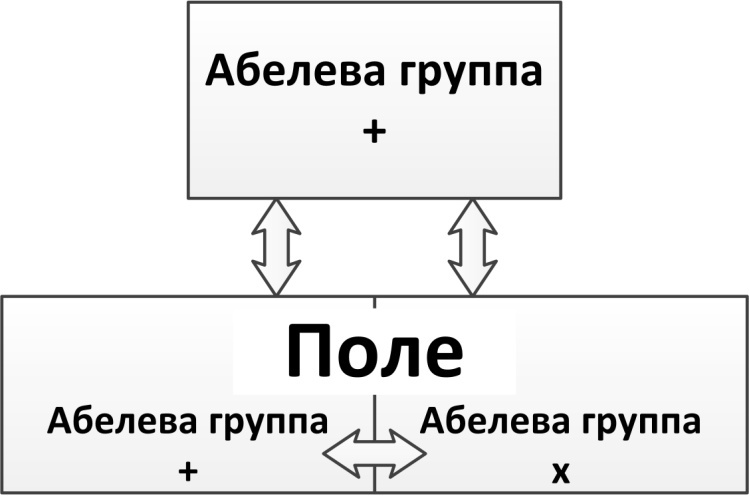
Определение 1. Линейной структурой 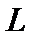(линейным пространством, векторным пространством) называют абелеву аддитивную группу (её элементы 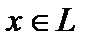называют векторами), определённую над полем произвольной природы (элементы поля называют скалярами 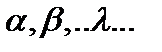), причём 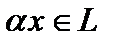, а естественное согласование между группой и полем обеспечивается аксиомами дистрибутивности: 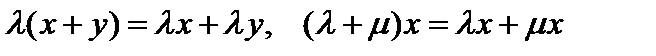, ассоциативности по элементам поля 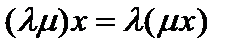и унитарности . Поле вещественных чисел 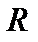и поле комплексных чисел 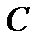называют основными полями, полагая, что поле 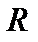стандартно вложено в поле 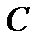. Если основное поле любое, то его обозначают буквой 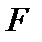. То есть линейная структура это четвёрка .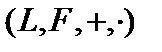

Комментарий. Для краткости обычно вместо 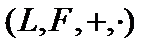говорят 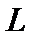. Если абелева аддитивная группа определена над любым кольцом, то такая структура называется модулем. Иногда под векторным пространством понимают абелеву аддитивную группу, определённую над телом. Дадим прямое определение линейной структуры

Определение 1^*. Множество 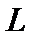называется линейным пространством (линейной структурой), если для любых двух его элементов x, y определен элемент 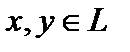(называемый суммой x и y), и для любого элемента 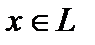и любого числа α определен элемент 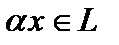, причем выполнены следующие условия:

1) для любых элементов 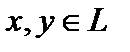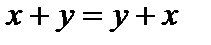(коммутативность сложения); 2) для любых элементов 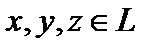(x+y)+z=x+(y+z) (ассоциативность сложения); 3) существует элемент 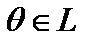(называемый нулевым элементом, или нулем пространства L) такой, что для любого элемента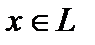 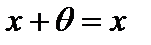(существование нулевого элемента); 4) для любого элемента 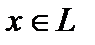существует элемент 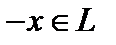(называемый обратным к x) такой, что 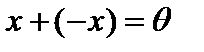(существование обратного элемента); 5) для любых элементов 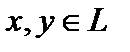и любого числа α α(x+y)=αx+αy (дистрибутивность умножения суммы элементов на число); 6) для любых чисел 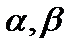любого элемента 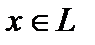(α+β)x=αx+βx (дистрибутивность умножения суммы чисел на элемент); 7) для любых (вещественных) чисел α, β и любого элемента 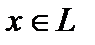(_αβ)x=α(βx) (ассоциативность умножения на число); 8) для любого элемента 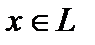1x=x (свойство единицы).

Примеры групп. Примерами групп являются целые, рациональные, действительные, комплексные числа по сложению, ненулевые рациональные, действительные, комплексные числа по умножению. Все эти группы являются абелевыми. Следующий пример групп возникает из векторных пространств. Пусть 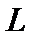— векторное пространство над полем F. Множество невырожденных линейных преобразований векторного пространства 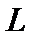образует группу. Легко проверить, что векторные пространства одинаковой размерности n над одним и тем же полем изоморфны пространству строк длины n, а множество невырожденных линейных преобразований совпадает с множеством невырожденных матриц.

Примеры колец. Множество полиномов образуют абелево кольцо с единицей (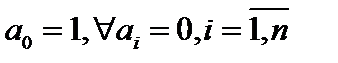),множество рациональных чисел (нет нейтрального и противоположного элементов по умножению).

Date: 2015-09-03; view: 469; Нарушение авторских прав