Полнота системы векторов в смысле Стеклова

Теорема 1. (О линейной независимости ортогональных векторов). Пусть 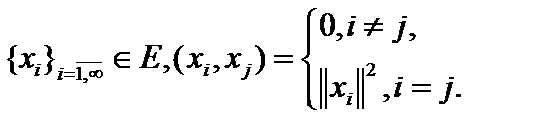Тогда система векторов 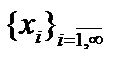линейно независима.

. Составим линейную комбинацию 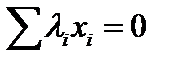и умножим её скалярно на 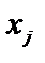: 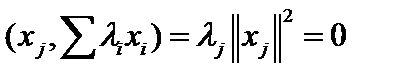, но .

Определение 1. Система векторов 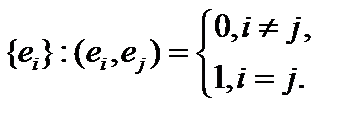или 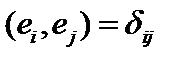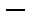символ Кронекера, называется ортонормированной (ОНС).

Определение 2. Для произвольного элемента 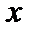произвольного бесконечномерного евклидова пространства и произвольной ортонормированной системы элементов 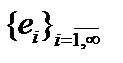рядом Фурье элемента 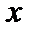по системе 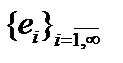называется формально составленная бесконечная сумма (ряд) вида 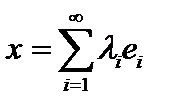в которой действительные числа 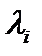называемые коэффициентами Фурье элемента 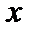по системе 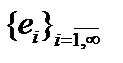, где .

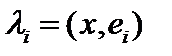Комментарий. Умножив элемент 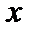скалярно на 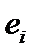и сразу получим, что 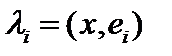. Естественно, возникает вопрос о сходимости этого ряда. Для исследования этого вопроса зафиксируем произвольный номер 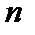и выясним, что отличает 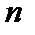-ю частичную сумму ряда Фурье от любой другой линейной комбинации 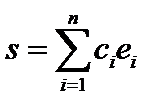первых 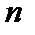элементов ортонормированной системы .

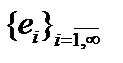Теорема 2. Для любого фиксированного номера 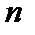среди всех сумм вида 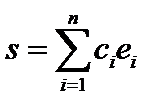наименьшее отклонение от элемента 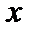по норме данного евклидова пространства имеет n-я частичная сумма ряда Фурье элемента 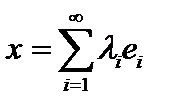при .

Учитывая ортонормированность системы 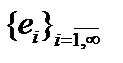иопределение коэффициента Фурье, можно записать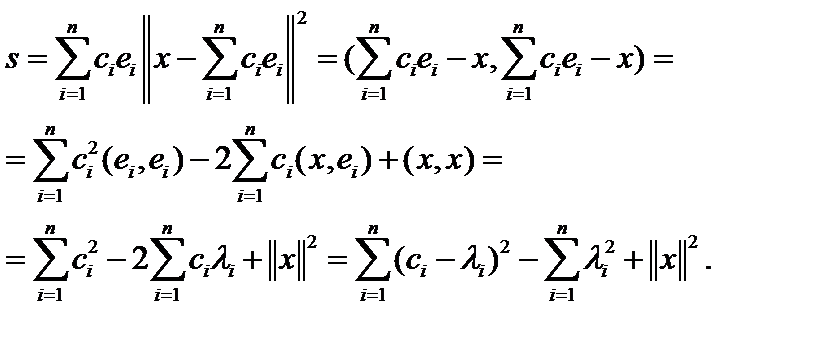

Минимум этого выражения при 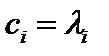так как при этом всегда неотрицательная первая сумма в правой части обращается в нуль, а остальные слагаемые от 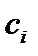не зависят.

Пример. Рассмотрим тригонометрическую систему: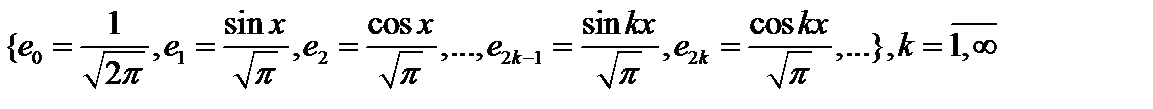

в пространстве всех интегрируемых по Риману функций на сегменте . Легко проверить, что это ОНС, и тогда Ряд Фурье функции 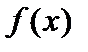имеет вид: 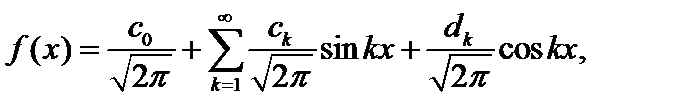где

.

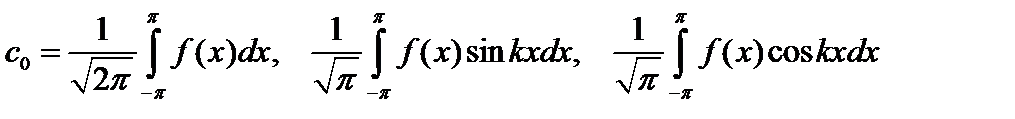Комментарий. Тригонометрический ряд Фурье обычно записывают в виде: 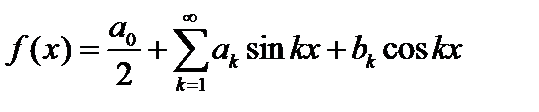. Тогда .

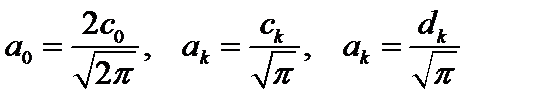Произвольная ОНС в бесконечномерном эвклидовом пространстве без дополнительных предположений, вообще говоря, не является базисом этого пространства. Рассмотрим ОНС 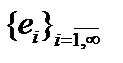где 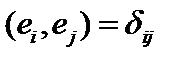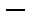символ Кронекера. в произвольном бесконечномерном эвклидовом пространстве 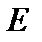. Пусть 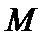– подпространство эвклидова пространства, а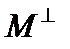 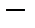подпространство, ортогональное к . Тогда эвклидово пространство 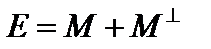. Проекция вектор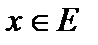а на 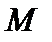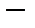вектор 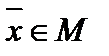, где .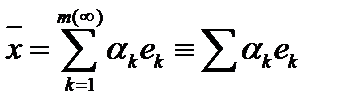

Мы будем искать те значения коэффициентов разложения 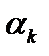, при которых невязка (квадрат невязки) 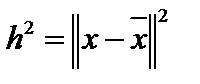будет минимальна:

.

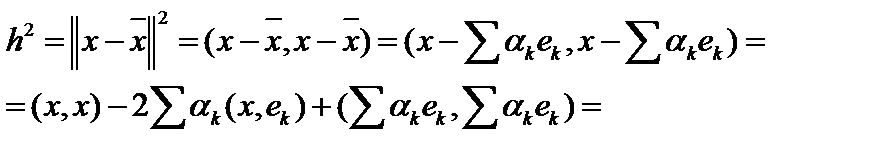
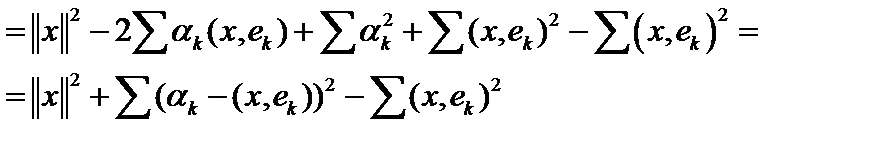Ясно, что это выражение будет принимать минимальное значение при 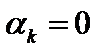, что тривиально, и при 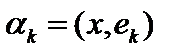. 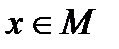Тогда 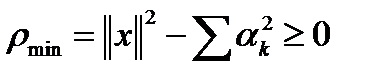. Отсюда получаем неравенство Бесселя 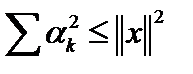. При ортонормированная система векторов (ОНС) называется полной ортонормированной системой в смысле Стеклова (ПОНС). Отсюда можно получить равенство Стеклова – Парсеваля теорему Пифагора для полныхв смысле Стеклова бесконечномерных эвклидовых пространств.

Определение 3. ОНС, для которой выполняется равенство Стеклова–Парсеваля 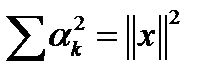называется полной ортонормированной системой в смысле Стеклова (ПОНС).

Определение 4. ПОНС называется ортонормированным базисом пространства (ОНБ). Определение 5. Полная ортонормированная система называется ортонормированным базисом пространства.

Пример. В эвклидовом пространстве последовательностей комплексных чисел 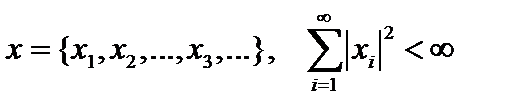ОНБ образует система векторов 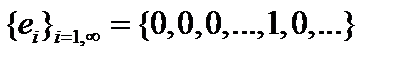. Рассмотрим для 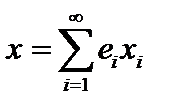частичную сумму ряда 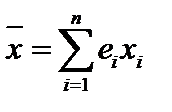. Тогда 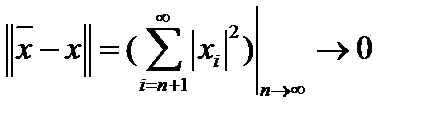как хвост сходящегося ряда. Таким образом, система векторов 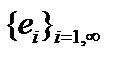является ПОНС и образуетОНБ.

Пример. Тригонометрическая система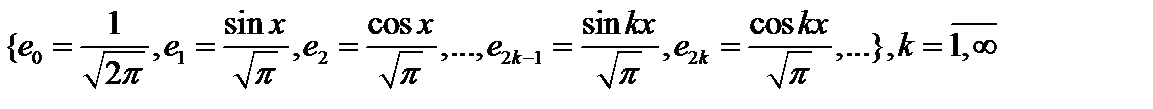

в пространстве всех интегрируемых по Риману функций 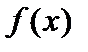на сегменте 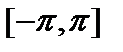является ПОНС и образуетОНБ.

Комментарий. Если 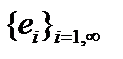– полная система векторов, то не существует отличных от нуля векторов из 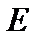, ей ортогональных, так как из 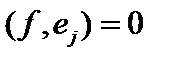для всех 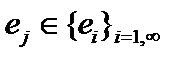следует 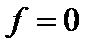. Пусть 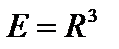. Выберем некоторый вектор . Он, очевидно, не образует полной системы векторов. Подпространство, им порождаемое, есть 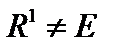, а ортогональное дополнение отлично от нуля и представляет собой плоскость, проходящую через нуль перпендикулярно 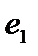(см. рис.а). Выберем в этой плоскости, то есть в ортогональном дополнении, элемент 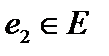и образуем последовательность 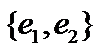. Она также не полна и порождает пространство 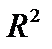, то есть плоскость, а ортогональное дополнение к ней вновь не нуль, а представляет собой прямую, перпендикулярную этой плоскости (см. рис.б). И наконец, когда мы выберем на этой прямой третий вектор , то последовательность 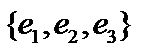станет полной, будет порождать пространство 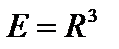, а ортогональное дополнение к ней станет нулевым (рис. в).

Теорема 3 (Грамм Шмидт об ортогонализации). Пусть 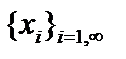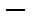линейно независимая система векторов эвклидова пространства 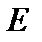. Тогда в пространстве 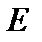существует ОНБ .

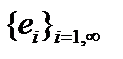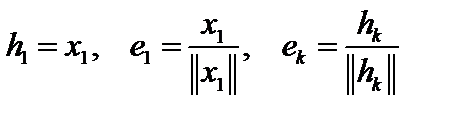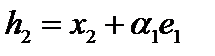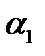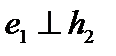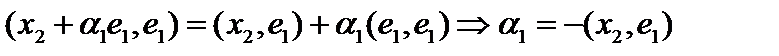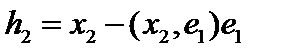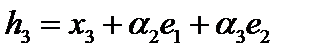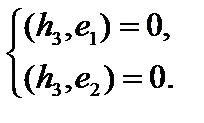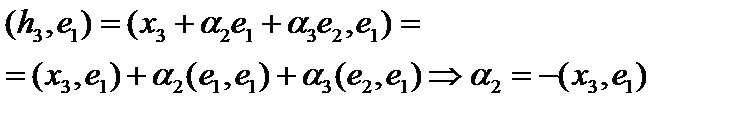Построим этот базис. Обозначим . Построим и выберем так, чтобы , то есть . Тогда . Построим вектор таким образом, чтобы Тогда , а 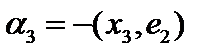Продолжая процедуру, получим 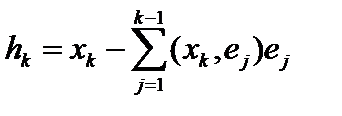.Эту формулу следует доказать методом матиндукции.

Пример. 1. Любую ортогональную систему векторов можно дополнить до ОНБ. Дополнить совокупность векторов 1) 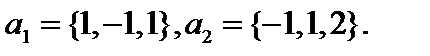2) 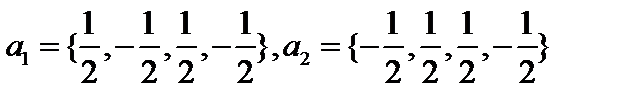до ОНБ.

2. Найти ОНБ линейной оболочки: .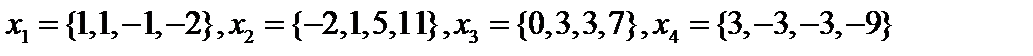

3. Ортогонализировать векторы 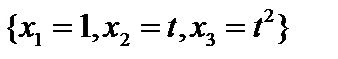в пространстве 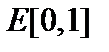, показав их линейную независимость. (Совокупность функций 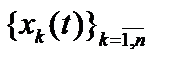линейно независима 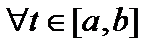, если и только если её вронскиан 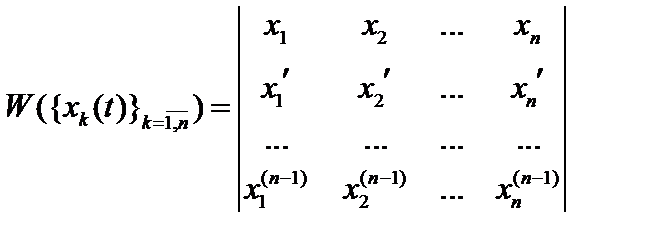не равен нулю.)

Комментарий. Ортогонализированная система векторо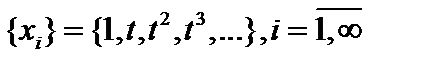в в 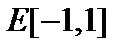называется полиномами Лежандра: 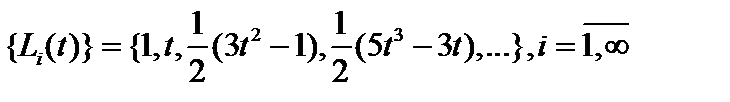, которые появляются при решении многих задач математической физики.

4. Ортогонализировать в 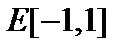систему векторов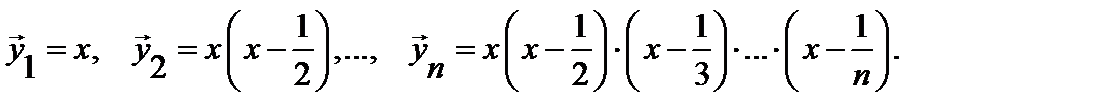

Date: 2015-09-03; view: 1002; Нарушение авторских прав