
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Алгебраические структуры
|
|
Определение 1. Пусть М и S два множества произвольной природы, a x,y,z -три элемента, быть может, разных множеств.
Правило (закон), по которому упорядоченной паре элементов х и у ставится в соответствие элемент z (один и только один), называется бинарной операцией или законом композиции, результат этой операции (элемент z) называется композицией, а элементы х и у называются операнды.
Определение 2. Если 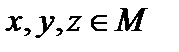 (одному из множеств), то закон композиции называется внутренним а множество М называется замкнутым относительно этого закона (этой бинарной операции).
(одному из множеств), то закон композиции называется внутренним а множество М называется замкнутым относительно этого закона (этой бинарной операции).
Определение 3. Если операнды принадлежат разным множествам, а композиции 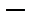 одному из них (например
одному из них (например 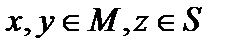 ), то такая бинарная операция называется внешним законом.
), то такая бинарная операция называется внешним законом.
Комментарий. На множестве М и S может быть определено несколько законов, но все многообразие ситуаций реализуется в простейшем случае, когда их не более двух. Один из них (произвольный) называется аддитивным и обозначается  , другой мультипликативный и обозначается
, другой мультипликативный и обозначается 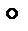 .
.
Множество натуральных чисел с обычными операциями сложения, умножения, возведения в степень - примеры внутренних законов, множество действительных чисел и множество векторов в конечномерном пространстве с операцией произведения числа на вектор 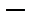 внешний закон. В этом пункте нас будут интересовать только внутренние законы композиции.
внешний закон. В этом пункте нас будут интересовать только внутренние законы композиции.
Определение 4. А лгебраической структурой 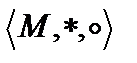 называется множество (носитель структуры) М с заданным на нём одним или двумя внутренними законами композиции, которые обозначаются
называется множество (носитель структуры) М с заданным на нём одним или двумя внутренними законами композиции, которые обозначаются  и
и 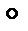 и часто называются “сложение” и “умножение”.
и часто называются “сложение” и “умножение”.
Комментарий. Эти законы композиции можно наделить или нет определенными свойствами, которые, в свою очередь, задают ту или иную структуру множества М, которое называется носителем а лгебраической структуры. Имея дело с а лгебраической структурой (АС), следует соблюдать три правила.
1. Природа и характер носителя АС не обсуждается.
2. Природа и характер операций, порождающих данную АС на
множестве М,не обсуждается.
3. Все рассуждения поводятся только на абстрактном уровне. На
уровне интерпретаций (примеров конкретных АС) утверждение может
быть верно, а на абстрактном уровне нет. Обратное 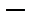 неверно.
неверно.
Свойства внутренних законов композиции:
1. 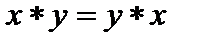
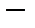 коммутативность.
коммутативность.
2. 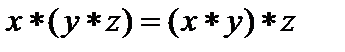
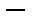 ассоциативность.
ассоциативность.
3. 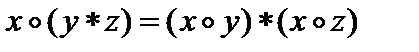
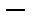 дистрибутивность
дистрибутивность
слева операции 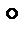 относительно операции
относительно операции  .
.
4. 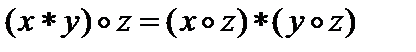
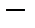 дистрибутивность справа операции
дистрибутивность справа операции 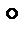 относительно операции
относительно операции  .
.
Аналогично определяется дистрибутивность относительно операции 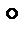 .
.
Примеры. 1. Множество действительных чисел с обычными операциями сложения и умножения. Эти операции коммутативны и ассоциативны. Кромке того 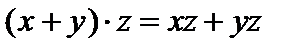 и
и 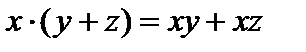 , то есть умножение дистрибутивно справа и слева относительно сложения. Но
, то есть умножение дистрибутивно справа и слева относительно сложения. Но 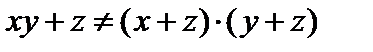 и
и 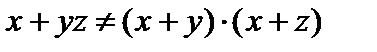 , то есть сложение не дистрибутивно ни справа, ни слева относительно операции умножения.
, то есть сложение не дистрибутивно ни справа, ни слева относительно операции умножения.
2. 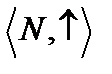
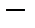 операция возведения в степень не ассоциативна, не коммутативна (
операция возведения в степень не ассоциативна, не коммутативна (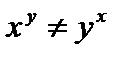 ,
, 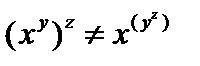 , но дистрибутивна справа относительно операции умножения (
, но дистрибутивна справа относительно операции умножения (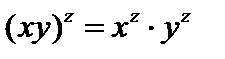 ) и вообще не имеет смысла дистрибутивность слева относительно умножения.
) и вообще не имеет смысла дистрибутивность слева относительно умножения.
3. Операции  и
и  для множеств взаимно дистрибутивны относительно друг друга, ассоциативны и коммутативны.
для множеств взаимно дистрибутивны относительно друг друга, ассоциативны и коммутативны.
Комментарий. Законы композиции наделяют элементы множества М некоторыми свойствами, верными или нет только при этих законах. Другими словами, на множестве М при действии данного закона с его свойствами появляются выделенные элементы, т.е. оно становится структуированным (откуда и понятие АС).
Определение 5. Элемент 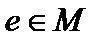 называется нейтральным относительно данного закона
называется нейтральным относительно данного закона  , если
, если 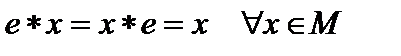 .
.
Примеры. Ноль на множествах  при сложении, единица при умножении,
при сложении, единица при умножении, 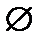 при объединении и при пересечении множеств.
при объединении и при пересечении множеств.
Ясно, что его может и не быть, например, на множестве 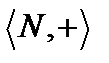 , или нейтральный элемент фактически может быть не определенным элементом множества, а образовывать целый класс элементов этого множества. Рассмотрим, например, множество остатков от деления натурального числа на 3 или, как говорят "вычетов по модулю три". Это множество состоит из классов чисел
, или нейтральный элемент фактически может быть не определенным элементом множества, а образовывать целый класс элементов этого множества. Рассмотрим, например, множество остатков от деления натурального числа на 3 или, как говорят "вычетов по модулю три". Это множество состоит из классов чисел 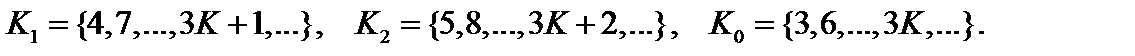 Зададим на этом множестве операцию + с помощью таблицы Кэли (способ задания операций для конечных множеств или классов множеств, заключающийся в непосредственном перечислении результатов операции).
Зададим на этом множестве операцию + с помощью таблицы Кэли (способ задания операций для конечных множеств или классов множеств, заключающийся в непосредственном перечислении результатов операции).
| + | К0 | К1 | К2 |
| К0 | К0 | К1 | К2 |
| К1 | К1 | К2 | К0 |
| К2 | К2 | К0 | К1 |
Видно, что 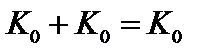 ,
, 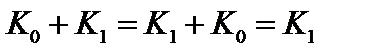 ,
, 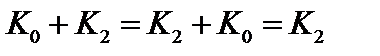 . Элемент К0- нейтральный, но фактически он представляет собой бесконечное множество натуральных чисел, нацело делящихся на три.
. Элемент К0- нейтральный, но фактически он представляет собой бесконечное множество натуральных чисел, нацело делящихся на три.
Теорема 1. Если нейтральный элемент есть, то он единственен.
 аа. Пусть
аа. Пусть 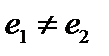 два нейтральных элемента относительно операции
два нейтральных элемента относительно операции  . Тогда
. Тогда  . Положив в первом равенстве
. Положив в первом равенстве 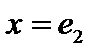 , получим
, получим  . Положив во втором равенстве
. Положив во втором равенстве 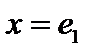 , получим
, получим 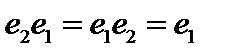 , то есть
, то есть 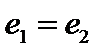 .■
.■
Определение 6. Пусть множество М содержит нейтральный элемент 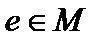 относительно операции
относительно операции  . Элемент
. Элемент 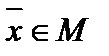 называется симметричным (обратным, противоположным) элементу
называется симметричным (обратным, противоположным) элементу 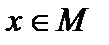 , если
, если 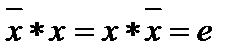 .
.
Примеры. На множестве (Z,+) нейтральный элемент 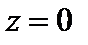 , а симметричным
, а симметричным 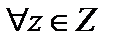 является элемент
является элемент 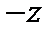 , на множестве
, на множестве 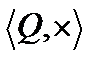 нейтральный элемент
нейтральный элемент 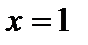 , но не все
, но не все 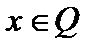 имеет симметричный элемент
имеет симметричный элемент 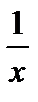 (
(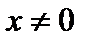 , то есть элемент
, то есть элемент 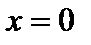 не имеет симметричного), на множестве
не имеет симметричного), на множестве 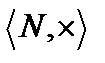 нейтральный элемент
нейтральный элемент 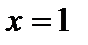 , а симметричного нет.
, а симметричного нет.
Естественно, нейтральный элемент группоида симметричен, самому себе, т.к. по определению как нейтрального так и симметричного элемента если 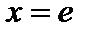 , тогда
, тогда 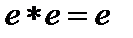 ,
, 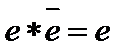 , то есть
, то есть 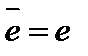 .
.
Определяя на множестве произвольной природы М один или два закона композиции, наделяя эти законы какими-то из перечисленных свойств и задавая структуру М относительно этих свойств, мы получим различные АС, перечисленные в таблице, задающей аксиомы АС.
| Название АС | I закон (аддитивный) | II закон мультипликативный) | |||||||
| ассо-циа-тив-ность | ком-мута-тив- ность | Нейт-раль-ный | сим- мет- ричный | ассо-циа-тив-ность | ком-мута-тив- ность | Нейт-раль-ный | сим- мет- ричный | ||
| Полугруппа | X | ||||||||
| Абелева полугруппа | X | X | |||||||
| Абелева полугруппа с нулем | X | X | X | ||||||
| Группа | X | X | X |
| Абелева группа | X | X | X | X | |||||
| Кольцо | X | X | X | X | X | ||||
| Абелево кольцо | X | X | X | X | X | X | |||
| Абелево кольцо с единицей | X | X | X | X | X | X | X | ||
| Тело | X | X | X | X | X | X | X | ||
| Поле | X | X | X | X | X | X | X | X |
Значёк Х означает, что данный закон обладает этими свойствами, а множество М имеет относительно этого закона соответствующие элементы. При этом полагается, что
1. Мультипликативный закон, если он определен,
дистрибутивен слева и справа относительно аддитивного.
2. Симметричный элемент мультипликативного закона
определен для всех элементов носителя АС (множества М),
кроме нейтрального относительно аддитивного закона.
Date: 2015-09-03; view: 1000; Нарушение авторских прав