Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Теорема об изменении количества движения для системы
|
|
Рассмотрим механическую систему из n точек. Пусть к каждой точке системы массой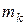 
и движущейся со скоростью 
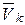приложены равнодействующая всех внешних 
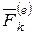и всех внутренних 
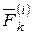сил. Применяя теорему об изменении количества движения для каждой точки системы (4.8), получим
, 
.
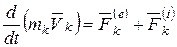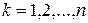Суммируя по всем точкам системы и учитывая, что сумма производных равна производной от суммы, получим
.
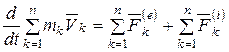Учитывая свойство внутренних сил системы (4.1) и определение количества движения (4.5) системы
, 
,
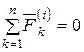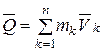получим
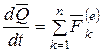. (4.11)
Формула (4.11) выражает теорему об изменении количества движения для системы в дифференциальной форме. Эта теорема формулируется следующим образом: производная по времени от вектора количества движения системы равна векторной сумме всех внешних сил, действующих на систему.
Проецируя (4.11) на оси декартовой системы координат, получим
,
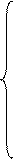
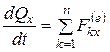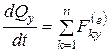, (4.11/)
.
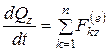Таким образом, производная по времени от проекции вектора количества движения системы на какую-либо координатную ось равна сумме проекций всех внешних сил системы на ту же ось.
Умножая обе части (4.11) на dt, получим
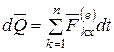. (4.12)
То есть дифференциал от вектора количества движения системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на рассматриваемую механическую систему.
Интегрируя (4.12) по времени от нуля до t, получим т еорему об изменении количества движения (теорему импульсов) для системы в конечной или интегральной форме
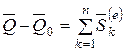, (4.13)
где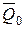 
– вектор количества движения системы в момент t 0 = 0,
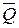– вектор количества движения системы в момент t,
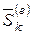– импульс внешней силы, действующей на k – ю точку за время t;
.
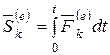Т еорема об изменении количества движения для системы в интегральной форме (4.13) формулируется следующим образом: изменение вектора количества движения системы за какое-либо время равно векторной сумме всех импульсов внешних сил, действующих на систему за то же время.
Проецируя (4.13) на оси декартовой системы координат, получим
, 
, 
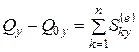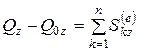. (4.13/)
Внешние силы системы не входят явно в теорему об изменении количества движения системы и, следовательно, не могут напрямую влиять на изменение количества движения системы. Они могут влиять на изменение количества движения только через внешние силы.
Date: 2015-09-03; view: 317; Нарушение авторских прав