
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Понятие о внутренних и внешних силах системы
|
|
Введем понятие внешних и внутренних сил механической системы.
Внешние силы механической системы 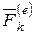 - это силы, с которыми действуют на точки рассматриваемой системы тела и точки, не входящие в рассматриваемую систему.
- это силы, с которыми действуют на точки рассматриваемой системы тела и точки, не входящие в рассматриваемую систему.
Внутренние силы механической системы 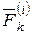 - это силы взаимодействия между точками рассматриваемой системы.
- это силы взаимодействия между точками рассматриваемой системы.
Внешние и внутренние силы могут включать в себя как активные силы, так и реакции связей.
Рассмотрим простейшее свойство внутренних сил, сформулированное как теорема о главном векторе и главном моменте внутренних сил системы.
Главный вектор и главный момент всех внутренних сил системы относительно произвольно выбранного центра равны нулю при любом состоянии системы.
Докажем эту теорему.
Рассмотрим систему, состоящую из n точек, где n – любое конечное число точек. Рассмотрим две произвольные точки системы A 1 и A 2 (рис. 11).
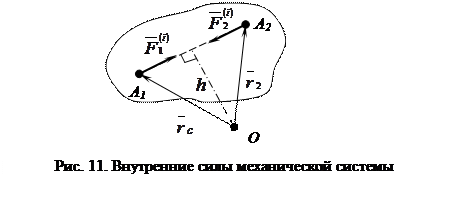 |
Так как силы действия и противодействия всегда равны друг другу по модулю, противоположны по направлению и действуют вдоль одной прямой линии соединяющей взаимодействующие точки, то для точек А 1 и А 2 справедливо равенство
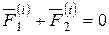 .
.
Главный вектор внутренних сил 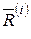 состоит из векторной суммы таких сил действия и противодействия, так как вся система состоит из пар взаимодействующих точек. Следовательно, для главного вектора, получим
состоит из векторной суммы таких сил действия и противодействия, так как вся система состоит из пар взаимодействующих точек. Следовательно, для главного вектора, получим
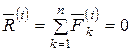 . (4.1)
. (4.1)
Проецируя на координатные оси, получим:
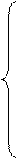
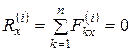 ;
;
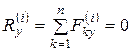 ; (4.1/)
; (4.1/)
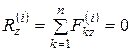 .
.
Внешние силы тоже являются силами взаимодействия, но для них силы действия приложены к точкам рассматриваемой системы, а силы противодействия приложены к телам и точкам не входящим в эту систему.
Рассмотрим теперь сумму моментов сил 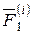 и
и 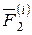 относительно произвольной точки O. Очевидно, что
относительно произвольной точки O. Очевидно, что
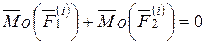 ,
,
так как обе силы имеют одинаковые плечи и противоположные направления векторных моментов.
Главный момент внутренних сил 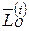 относительно точки O состоит из векторной суммы таких выражений, равных нулю, поэтому получим
относительно точки O состоит из векторной суммы таких выражений, равных нулю, поэтому получим
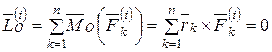 . (4.2)
. (4.2)
Проецируя на оси координат, получим
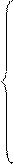 |
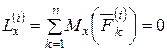 ,
,
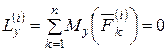 , (4.2/)
, (4.2/)
 .
.
2. Дифференциальные уравнения движения системы
Пусть известны внутренние и внешние силы, действующие на систему, состоящую из n точек. В каждой точке системы заменим действие внешних сил равнодействующей 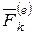 , а действие внутренних сил равнодействующей
, а действие внутренних сил равнодействующей 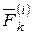 (рис. 13). Тогда для произвольной k –й точки системы дифференциальное уравнение движения в векторной форме на основании формулы (2.2) примет вид
(рис. 13). Тогда для произвольной k –й точки системы дифференциальное уравнение движения в векторной форме на основании формулы (2.2) примет вид
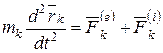 ;
; 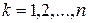 . (4.3)
. (4.3)
Систему n дифференциальных уравнений (4.3) называют дифференциальными уравнениями движения механической системы в векторной форме.
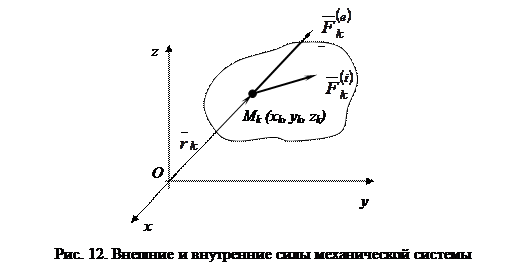 |
Если спроектировать систему векторных дифференциальных уравнений (4.3) на прямоугольные декартовы оси координат, то получим систему 3 n дифференциальных уравнений, описывающих движение точек механической системы.
Для нахождения движения механической системы по заданным силам и начальным условиям нужно проинтегрировать систему 3 n дифференциальных уравнений. Эту задачу в общем виде не удается точно решить даже для одной точки. Она исключительно сложна в случае двух материальных точек и неразрешима для системы трех взаимодействующих точек.
В некоторых случаях из дифференциальных уравнений движения системы можно получить первые интегралы соотношения, в которые не входят производные второго порядка от координат по времени.
Если известны первые интегралы, то задача интегрирования системы дифференциальных уравнений упрощается. Первые интегралы не всегда могут полностью описать движения всех точек системы, но характеризуют важные стороны движения системы в целом.
Первые интегралы удобно получать из так называемых общих теорем динамики. Общие теоремы являются следствиями системы дифференциальных уравнений движения точки или соответственно системы точек. Даже когда из общих теорем нельзя определить первые интегралы, они дают ценную информацию о движении точки или системы.
Date: 2015-09-03; view: 627; Нарушение авторских прав