Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Определения и общие формулы
|
|
Моментом инерции массы системы относительно точки (полюса) O называется сумма произведений масс точек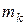 
на квадраты их расстояний 
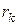до точки O. Момент инерции массы системы относительно точки определяют по формуле
(3.3)
Моментом инерции массы системы относительно оси Oz называется сумма произведений масс точек 
на квадраты их расстояний 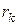до оси Oz. Момент инерции массы системы относительно оси определяют по формуле
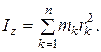(3.4)
Моментом инерции массы системы относительно плоскости xOy называется сумма произведений масс точек 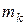на квадраты их расстояний 
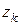до плоскости xOy. Момент инерции массы системы относительно плоскости определяют по формуле
(3.5)
Моментом инерции массы твердого тела относительно какой-либо оси Oz является предел суммы произведений всех элементов массы тела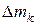 
на квадраты соответствующих расстояний 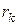до этой оси Oz при условии, что каждый элемент массы стремится к нулю. Момент инерции массы твердого тела относительно плоскости определяют по формулам
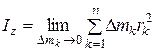, (3.6)
. (3.7)
В Международной системе единиц момент инерции измеряется в кг · м2,
.
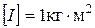При решении задач момент инерции твердого тела относительно оси представляют как произведение массы тела на квадрат некоторого расстояния, называемым радиусом инерции,
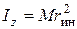. (3.8)
где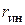 
– радиус инерции тела относительно оси,
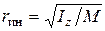. (3.9)
Учитывая зависимость радиус-вектора точки от ее координат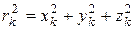 
, для момента инерции механической системы относительно начала координат по формуле (3.3) получим,
,
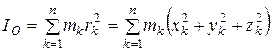где 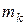- масса k -й точки системы,
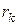- радиус вектор k -й точки системы,
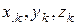- координаты k -й точки системы.
Осевые моменты инерции системы можно выразить формулами
; 
; 
.
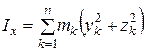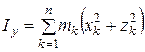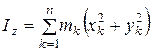Складывая осевые моменты инерции, получим
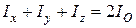. (3.10)
Формула (3.10) выражает связь между моментами инерции относительно осей координат и моментом инерции относительно начала координат.
Date: 2015-09-03; view: 428; Нарушение авторских прав