Теорема о моментах инерции относительно параллельных осей

(Теорема Штейнера)

Рассмотрим моменты инерции механической системы относительно осей параллельных систем координат (рис. 10). Рассмотрим две системы прямоугольных взаимно параллельных осей Oxyz и Cx ^/ y ^/ z ^/.

Пусть начало системы координат Cx ^/ y ^/ z ^/ находится в центре масс механической системы, в точке С.

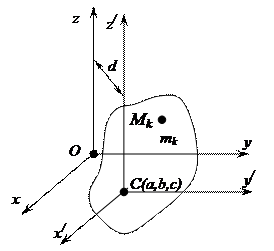Рис. 10. Моменты инерции относительно координатных осей

По определению момента инерции относительно оси, получим

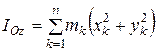
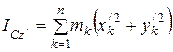
где 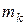– масса точки ,

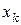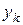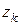, , – координаты точки относительно системы координат Oxyz,

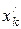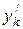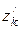, , – координаты точки 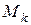относительно системы координат Cx^/y^/z^/.

Обозначим координаты центра масс механической системы, точки С, относительно осей координат Oxyz как a, b, c. Тогда, для взаимно параллельных осей координаты одной и той же точки связаны следующими соотношениями параллельного переноса:

, , .

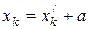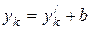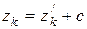Подставив эти выражения координат в выражение момента инерции 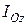после преобразований, получим

,

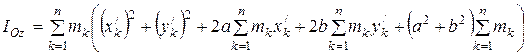где 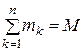– масса системы,

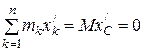– так как ,

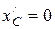– так как ,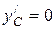

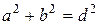– расстояние между осями Oz и Cz ^/.

Учитывая приведенные выражения окончательно, получим

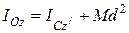. (3.11)

Формула (3.11) выражает теорему Штейнера, устанавливающую зависимость моментов инерции относительно параллельных осей, одна из которых проходит через центр масс.

Момент инерции системы относительно произвольной оси равен сумме момента инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями.

Date: 2015-09-03; view: 684; Нарушение авторских прав