Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Вторая основная задача динамики материальной точки
|
|
Вторую основную задачу динамики материальной точки формулируют следующим образом: по заданной массе и действующей на точку силе необходимо определить закон движения, а также траекторию этой точки.
Рассмотрим решение этой задачи в декартовой прямоугольной системе координат.
В общем случае сила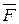 
, а следовательно, и ее проекции на координатные оси, зависят от времени, координат движущейся точки и ее скорости. Поэтому уравнения (2.3) принимают вид
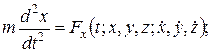
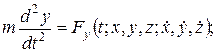(2.3/)
.
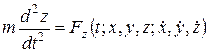Из теории дифференциальных уравнений известно, что решение одного дифференциального уравнения второго порядка содержит две произвольные постоянные. Для системы трех дифференциальных уравнений (2.3/) очевидно будет шесть произвольных постоянных: С 1, С 2, С 3, С 4, С 5, С 6.
Таким образом, после интегрирования системы (2.3/) получаем, что каждая из координат движущейся точки x, y, z зависит от времени t и шести произвольных постоянных:
 |
,
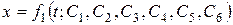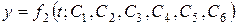, (2.5)
.
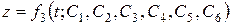Продифференцировав уравнения (2.5) по времени, определяют проекции скорости точки на координатные оси по формулам:
 |
.
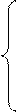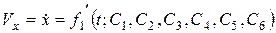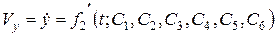, (2.6)
.
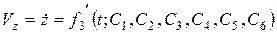Таким образом, задание силы не определяет конкретного движения материальной точки, а выделяет целый класс возможных движений, характеризующийся шестью произвольными постоянными. Действующая сила определяет только ускорение движущийся точки, а ее скорость и положение на траектории зависят от начальных условий по времени (начальное положение и начальная скорость (рис. 4)), которые имеют вид
|
; 
, 
, 
;
, 
, 
.
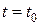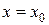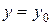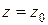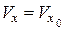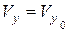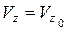Используя начальные условия (2.7), а также системы (2.5) и (2.6), получаем шесть уравнений для определения шести произвольных постоянных:
 |
|
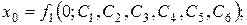
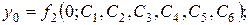
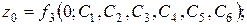
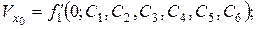
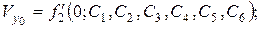
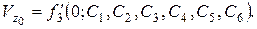
В общем случае задача интегрирования системы трех обыкновенных дифференциальных уравнений второго порядка (2.3/) является довольно сложной. Поэтому, если возможно интегрирование этой системы производят в два этапа. Рассмотрим эти этапы.
1. Первый этап – этап первых интегралов (уровень скоростей).
Представим систему уравнений (2.3/) в виде
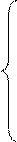
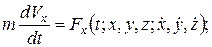
(2.3//)
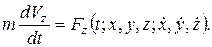
В результате интегрирования системы (2.3//) определяются проекции скоростей на оси декартовой системы координат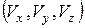 
. Эти проекции называются первыми интегралами системы. Они содержит три произвольных постоянных С 1, С 2, С 3:
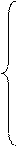
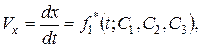
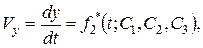(2.3///)
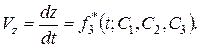
Постоянные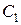 
, 
, 
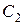определяют из начальных условий по времени (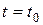
; 
, 
, 
).
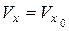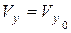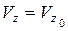2. Второй этап (уровень координат).
На втором этапе интегрируют систему уравнений (2.3///) и определяют закон движения точки в координатной форме. Это решение содержит еще три произвольных постоянных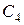 
, 
, 
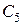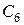и имеет вид
 |
,
,
.
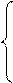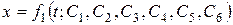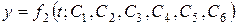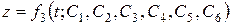Постоянные ,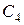 
, 
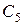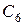определяются из начальных условий по времени (; 
, 
, 
).
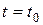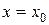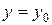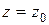Date: 2015-09-03; view: 405; Нарушение авторских прав