Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Решения. 1.Так как х0=1, то разложение будет по степеням (х-1), поэтому преобразуем исходную функцию следующим образом:
|
|
1) 
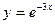, х0=1.
1.Так как х0=1, то разложение будет по степеням (х-1), поэтому преобразуем исходную функцию следующим образом:
= 
= 
.
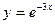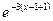Теперь обратимся к таблице «Разложения в ряд Маклорена некоторых элементарных функций». В стандартном разложении функции 
заменяем х на 
.
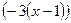Получаем:
Полученный ряд умножаем на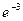 
:
= = 
.
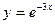2. Определим радиус сходимости полученного ряда.
Известно, что ряд 
(это ряд для функции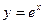 
) сходится при 
.
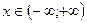В нашем случае: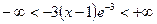 
. Откуда получаем 
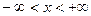– интервал сходимости, то есть ряд 
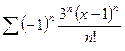сходится на всей числовой оси.
2) 
, х0=-3.
1. Подготовим функцию к разложению по степеням (х+3) и воспользуемся уже «готовым» разложением в ряд Маклорена функции 
.
.
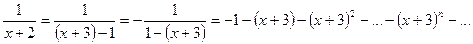2. Определим радиус сходимости полученного ряда.
Известно, что ряд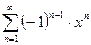 
(это ряд для функции ) сходится при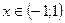 
. В нашем случае 
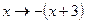, тогда 
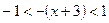. Решая, получаем: 
. Итак, интервал сходимости: 
. Радиус сходимости равен 1.
3) 
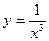, х0=4.
1. = 
= 
= 
.
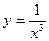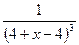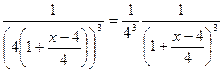Используем биномиальный ряд. В нашем случае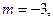 
. Получаем:
= 
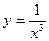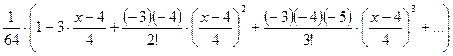
2. Определим радиус сходимости полученного ряда.
Как известно, биномиальный ряд сходится при 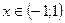. Получаем:
.
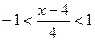
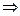
Итак, интервал сходимости: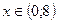 
. Радиус сходимости равен 4.
4) 
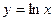, х0=3.
1. Преобразуем исходную фнкцию следующим образом:
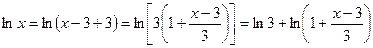. Теперь в разложении функции 
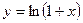заменим х на 
и к результату прибавим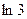 
. Получаем:
= 
.
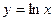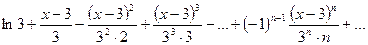2. Определим радиус сходимости полученного ряда.
Ряд 
для функции 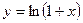сходится при 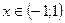. Значит, наш ряд сходится при 
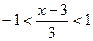. Решая это неравенство, получаем интервал сходимости: 
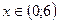. Радиус сходимости равен 3.
5. Вычислить приближенное значение (заданной под номером N5) функции в данной точке х, используя разложение этой функции в ряд Маклорена и, отбросив все слагаемые, начиная с х6. Результат округлить до 10-3 и сравнить с точным значением функции, вычисленным непосредственно или при помощи таблиц, если:
1) 
, 
;
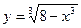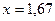2) 
, 
.
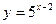Date: 2015-09-02; view: 369; Нарушение авторских прав