Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Решения. Проверяем выполнение признака Лейбница:
|
|
1) 
.
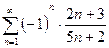Проверяем выполнение признака Лейбница:
Члены ряда по модулю образуют убывающую последовательность:
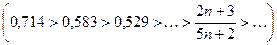
Но предел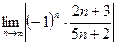 
= 
= 
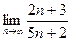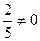
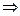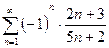ряд – расходится.
2) 
.
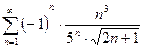1. Проверяем выполнение признака Лейбница:
Члены ряда по модулю образуют убывающую последовательность:
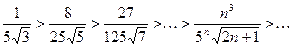вычислим приближенно на калькуляторе: 
, 
, 
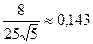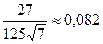, … и т.д. Несмотря на то, что в начале ряда его члены не образуют убывающую последовательность, следует иметь в виду, что «хвост» ряда все равно будет состоять из таких членов, которые все-таки образуют убывающую последовательность. Это видно из формулы общего члена, взятого по модулю:
.
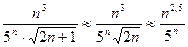Из двух функци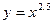й 
и 
«быстрее растет» . Значит, при увеличении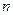 
знаменатель дроби 
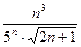всегда больше числителя, следовательно, сама дробь уменьшается.
Находим предел:
= 
= 
=
= 
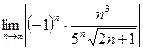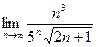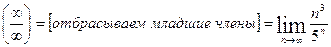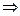ряд сходится по признаку Лейбница.
2. Составляем ряд из абсолютных величин чденов данного ряда и исследуем его сходимость.
.
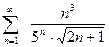Используем признак Даламбера:
= 
= 
= 
= 
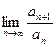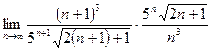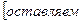
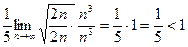– ряд сходится.
3.Вывод: исходный ряд 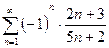– сходится абсолютно.
3) 
.
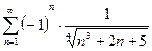1. Проверяем выполнение признака Лейбница:
Члены ряда по модулю образуют бесконечно убывающую последовательность:
При увеличении 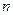числитель дроби 
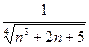становится все больше, значит, сама дробь – все меньше.
Находим предел:
= 
= 
= 
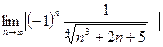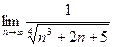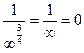
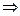ряд сходится по признаку Лейбница.
2. Проверим сходимость соответствующего знакоположительного ряда.
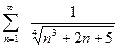
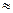
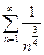– ряд расходится как обобщенный гармоничский с показателем 
.
3. Вывод: исходный ряд 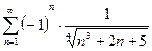– сходится условно.
3. Найти радиус сходимости степенного ряда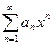 
с заданным (под номером N3) коэффициентом 
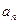. Проверить сходимость (абсолютную и условную) этого ряда в концах интервала сходимости, если:
1) 
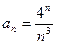; 2) 
; 3)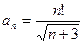 
.
Date: 2015-09-02; view: 398; Нарушение авторских прав