Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Решения
|
|
1) 
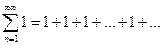расходится, т.к. 
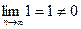(выполнен необходимый признак сходимости).
2) 
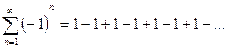– расходится, т.к. 
не существует (то есть 
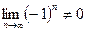точно, значит, выполнен необходимый признак сходимости).
3) 
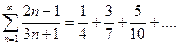– расходится, т.к. 
.
4) 
, 
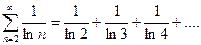ряд может сходиться, но может и расходиться. Необходимый признак сходимости ответа не дал. Пробуем применить какой-либо из достаточных признаков, например, признак сравнения. Для этого сравним наш ряд с рядом 
, про который уже известно, что он расходится (это гармонический ряд, см. таблицу «эталонные ряды»).
Очевидно, что при 
выполняется следующее соотношение
.
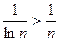Меньший ряд расходится, следовательно, расходится и больший ряд .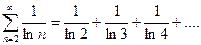
5) 
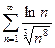– ряд сходится, т.к. 
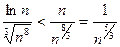при , а ряд 
– сходится как обобщенный гармонический с показателем 
.
6) 
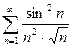– ряд сходится, т.к. 
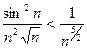, а ряд 
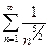– сходится как обобщенный гармонический с показателем 
.
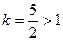7) 
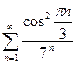– ряд сходится, т.к. 
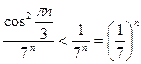при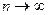 
, а ряд 
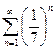– сходится как геометрический при 
.
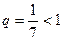8) 
– ряд расходится, т.к. члены его для достаточно больших n эквивалентны членам обобщенного гармонического ряда:
,
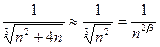а ряд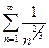 
– расходится (показатель 
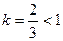). Применили 2-ой признак сравнения (предельный).
Итак: 
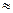
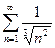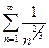= – расходится как обобщенный гармоничский с показателем .
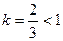9) 
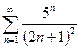. Здесь уместно применить признак Даламбера.
, 
.
= 
= 
= 
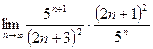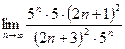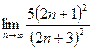– ряд расходится.
10) 
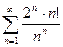. По признаку Даламбера
= 
= 
= 
=
= 
= 
= 
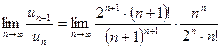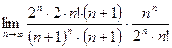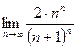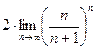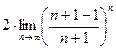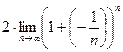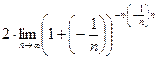=(по 2-му замечательному пределу)= 
= 
= 
= 
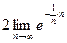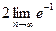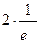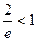
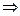исходный ряд сходится.
11) 
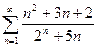. Применяя признак Даламбера, можно предварительно упростить выражение для общего члена ряда, оставля только главные члены. В знаменателе оставим 2n, т.к. показательная функция 
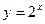«растет быстрее», чем линейная функция 
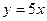. В числителе оставим 
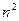. Получаем:
.
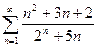
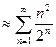Найдем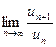 
= 
= 
= 
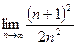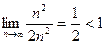– ряд сходится.
12) 
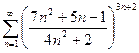. По признаку Коши (радикальному):
= 
= 
= 
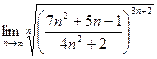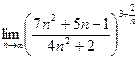ряд расходится.
13) 
. Применим интегральный признак Коши. Для этого найдем несобственный интеграл. Для этого сначала найдем соответствующий неопределенный интеграл:
= 
=
= 
= 
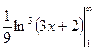– интеграл и вместе с ним исходный ряд расходятся.
2. Исследовать на абсолютную и условную сходимость знакочередующийся ряд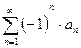 
с заданным (под номером N2) общим членом 
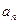, если:
1) 
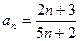; 2) 
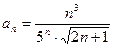; 3)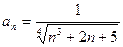 
.
Date: 2015-09-02; view: 307; Нарушение авторских прав