Теорема Абеля

Если степенной ряд сходится при х=х₁, то он сходится для всех .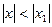

Если степенной ряд расходится при х=х₂, то он расходится для всех .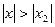

Из теоремы Абеля следует, что существует такое значение 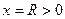, что для 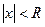степенной ряд сходится, а для 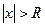расходится.

Это число R называется радиусом сходимости степенного ряда.

Интервал называется интервалом сходимости.

Ряд вида

называется степенным рядом общего вида. Для такого ряда интервал сходимости опрделяется неравенством 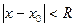, то есть интервал сходимости: .

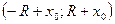Радиус сходимости может быть равен нулю, и тогда ряд сходится только в одной точке, но может быть и неограниченно большим 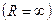. В последнем случае ряд сходится на всей числовой оси.

Для нахождения интервала сходимости степенного ряда удобно пользоваться достаточными признаками сходимости знакоположиельных рядов и, в частности, признаками Даламбера и Коши. В соответствии с этими признаками степенной ряд сходится, ес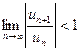ли

или .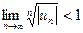

Эти условия и применяются для нахождения интервала сходимости степенного ряда.

Отметим, что нахождение интервала сходимости также включает и проверку сходимости ряда на концах полученного интервала.

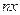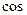
Замечание. При нахождении интервала сходимости рядов, содержащих выражения типа , и т.п. можно предварительно упростить выражение для общего члена ряда, используя таблицу эквивалентных бесконечно малых величин. Если же в выражение для общего члена ряда входят , , 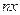таблицей эквивалентных бесконечно малых величин пользоваться нельзя, так как аргумент не является бесконечно малой величиной. В таких случаях полезными могут оказаться оценки: , , .

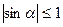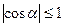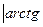
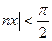Таблица эквивалентных бесконечно малых величин.

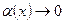
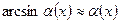
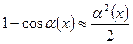
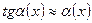
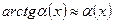
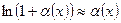
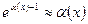
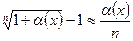
Date: 2015-09-02; view: 311; Нарушение авторских прав