Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Решения. 1. Используем признак Даламбера
|
|
1) 
.
1. Используем признак Даламбера. Составим предел отношения последующего члена ряда к предыдущему и потребуем, чтобы он был по модулю меньше единицы.
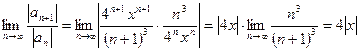. Теперь потребуем, чтобы 
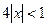откуда 
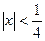. Получаем интервал значений х, в котором ряд сходится 
.
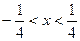2. Проверяем сходимость ряда на концах интервала. Для этого подставляем значения 
в исходный ряд, получаем числовой ряд и исследуем его сходимость одним из признаков сходимости числовых рядов.
А) При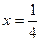 
имеем ряд = 
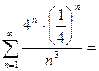
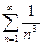. Данный ряд сходится как обобщенный гармонический с показателем 
.
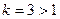Б) При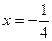 
имеем ряд = 
= 
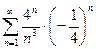. Данный ряд сходится абсолютно, т. к. сходится соответствующий знакоположительный ряд.
3. Вывод: оба конца интервала принадлежат интервалу сходимости, т.е. ряд сходится в закрытом интервале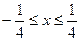 
.
2) 
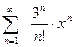. Воспользуемся признаком Даламбера.
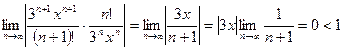. Предел равен нулю для любых значений х, поэтому ряд сходится на всей числовой прямой 
.
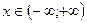3) 
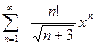. По признаку Даламбера 
= 
=
= 
= 
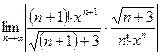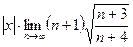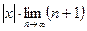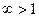. Ряд расходится на всей числовой оси, кроме одной точки 
.
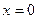4. Разложить данную (под номером N4 ) функцию в ряд Тейлора в заданной точке х0 и определить радиус сходимости полученного ряда, если:
1) 
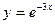, х0=1; 2) 
, х0=-3; 3)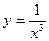 
, х0=4; 4) 
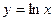, х0=3.
Date: 2015-09-02; view: 421; Нарушение авторских прав