
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Інтегрування раціональних функцій
|
|
Нагадаємо, що раціональною функцією або раціональним дробом називається відношення многочленів:
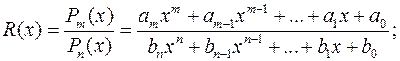
де  - многочлен степеня
- многочлен степеня  , а
, а  - многочлен степеня
- многочлен степеня 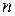 . Якщо
. Якщо 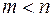 , то раціональний дріб називається правильним, в противному разі
, то раціональний дріб називається правильним, в противному разі 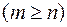 - неправильним. З неправильного раціонального дробу можна завжди виділити цілу частину (многочлен), подавши даний дріб у вигляді суми многочлена і правильного раціонального дробу. Оскільки інтеграл від многочлена обчислюється безпосереднім інтегруванням, то задача інтегрування будь-якої раціональної функції зводиться до інтегрування правильного раціонального дробу.
- неправильним. З неправильного раціонального дробу можна завжди виділити цілу частину (многочлен), подавши даний дріб у вигляді суми многочлена і правильного раціонального дробу. Оскільки інтеграл від многочлена обчислюється безпосереднім інтегруванням, то задача інтегрування будь-якої раціональної функції зводиться до інтегрування правильного раціонального дробу.
Раніше було показано, що правильний раціональний дріб завжди можна розкласти на суму простих дробів чотирьох типів. В результаті інтеграл від правильного раціонального дробу подається у вигляді суми інтегралів від простих дробів і таким чином обчислення інтеграла від раціональної функції зводиться до обчислення інтегралів від простих дробів.
Розглянемо ці інтеграли.
1) Простий дріб 1 типу:
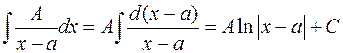 .
.
2) Простий дріб 2 типу:
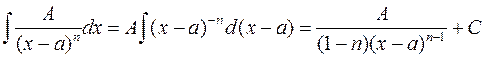 .
.
3) Простий дріб 3 типу:
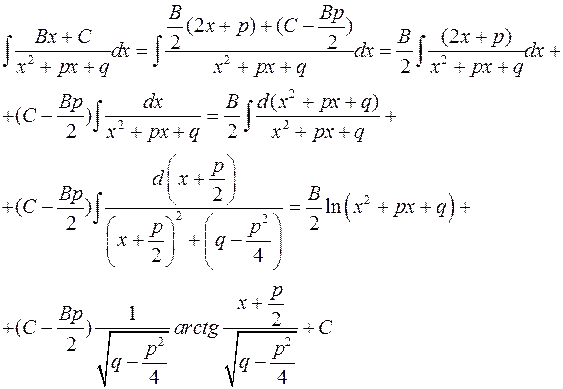
Зазначимо, що тут тричлен 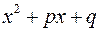 не має дійсних коренів, тому його дискримінант
не має дійсних коренів, тому його дискримінант  а значить
а значить 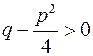 .
.
4) Простий дріб 4 типу:
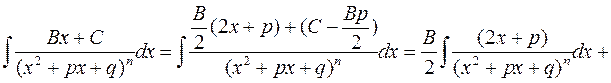
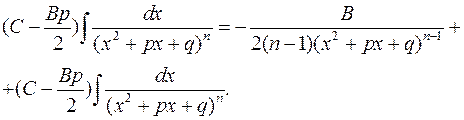

Щоб завершити обчислення інтеграла потрібно обчислити інтеграл у правій частині. Для цього існує формула зниження степеня (рекурентна формула):
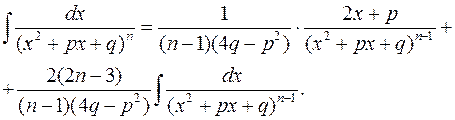
Повторне застосування цієї формули приводить кінець кінцем до інтеграла 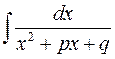 , який обчислюється як показано вище.
, який обчислюється як показано вище.
Таким чином кожен простий дріб має первісну, яка виражається в скінченному вигляді через елементарні функції: раціональну функцію, логарифм і арктангенс. Це означає, що будь-яка раціональна функція за встановленим алгоритмом інтегрується в елементарних функціях. Якщо підінтегральна функція не є раціональною, але можна вказати підстановку, яка приводить заданий інтеграл до інтеграла від раціональної функції, то цим задача обчислення інтеграла цілком розв’язується (інтеграл, як кажуть, «раціоналізується»).
Приклад. Знайти інтеграл 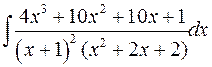 .
.
Під знаком інтеграла правильний раціональний дріб, розкладемо його в суму простих дробів

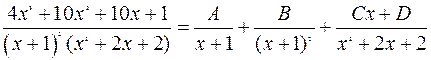 .
.
Зведемо праву частину до спільного знаменника і прирівняємо чисельники лівої і правої частини:
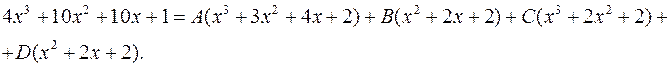 Порівнюючи коефіцієнти при однакових степенях
Порівнюючи коефіцієнти при однакових степенях 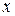 , отримуємо систему рівнянь
, отримуємо систему рівнянь
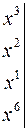
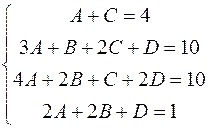 .
.
Розв’язок цієї системи 
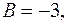

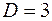 .
.
Тоді 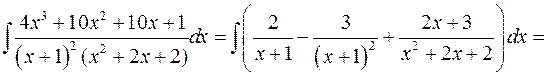
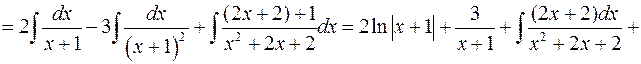
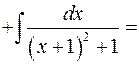
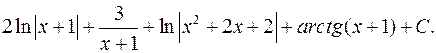
6. Інтегрування деяких ірраціональних функцій
Означенн я. Раціональною функціє  від
від 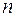 змінних
змінних  називається така функція, в якій над цими змінними і сталими числами виконується скінченне число чотирьох арифметичних дій.
називається така функція, в якій над цими змінними і сталими числами виконується скінченне число чотирьох арифметичних дій.
Наприклад, раціональною функцією відносно змінних 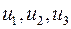 є функція
є функція 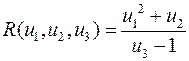 .
.
Якщо змінні 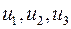 в свою чергу є функціями від
в свою чергу є функціями від 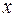 , то ми говоримо про раціональну функцію відносно цих функцій. Так, функція
, то ми говоримо про раціональну функцію відносно цих функцій. Так, функція 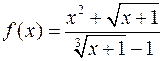 є раціональною функцію від функцій
є раціональною функцію від функцій 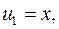
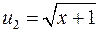 ,
, 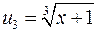 , тобто
, тобто 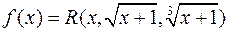 але відносно змінної
але відносно змінної 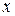 ця функція не є раціональною.
ця функція не є раціональною.
Розглянемо деякі випадки, коли інтеграли від ірраціональних функцій належною підстановкою зводяться до інтегралів від раціональних функцій («раціоналізуються»).
1) Інтеграли вигляду 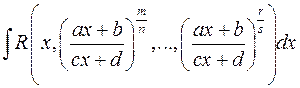 раціоналізуються підстановкою
раціоналізуються підстановкою 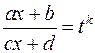 , де
, де 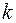 - спільний знаменник дробів
- спільний знаменник дробів 


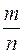 ,…,
,…, 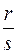 .
.
Справді, якщо 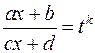 , то виражаючи
, то виражаючи 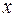 через
через 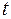 , одержуємо
, одержуємо 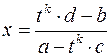 ,
, 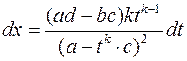 тобто
тобто 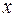 і
і 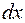 виражаються через раціональні функції від
виражаються через раціональні функції від 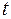 . Далі, кожний степінь дробу
. Далі, кожний степінь дробу  виражається через цілий степінь змінної
виражається через цілий степінь змінної 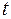 , і в результаті підінтегральна функція перетворюється в раціональну функцію від
, і в результаті підінтегральна функція перетворюється в раціональну функцію від  , що і було метою підстановки.
, що і було метою підстановки.
Приклад. Знайти інтеграл  .
.
Виконаємо заміну змінної, поклавши 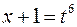 , тоді
, тоді  ,
, 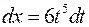 .
.
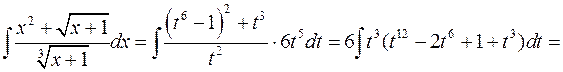
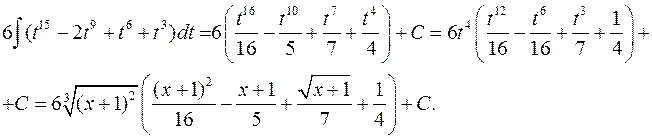
2) Інтеграли вигляду 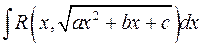 .
.
Якщо тричлен 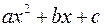 має дійсні корені
має дійсні корені  і
і 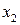 , то
, то  , і інтеграл приймає вигляд
, і інтеграл приймає вигляд 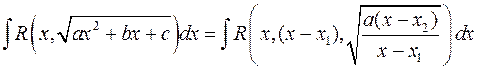 , а це інтеграл уже розглянутого вигляду. Як у цьому випадку, так і у випадку відсутності дійсних коренів у тричлена
, а це інтеграл уже розглянутого вигляду. Як у цьому випадку, так і у випадку відсутності дійсних коренів у тричлена 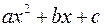 , даний інтеграл можна раціоналізувати за допомогою підстановок Ейлера:
, даний інтеграл можна раціоналізувати за допомогою підстановок Ейлера:
1) якщо 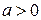 , то
, то 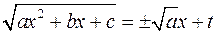 .
.
2) Якщо 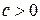 , то
, то 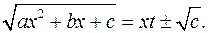
Приклад. Знайти інтеграл 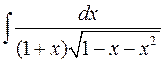 . Застосуємо другу підстановку Ейлера:
. Застосуємо другу підстановку Ейлера: 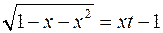 , тоді
, тоді 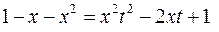 , звідки
, звідки 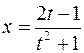 ,
,  ,
, 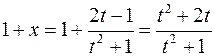 ,
, 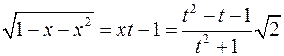 .
.
В результаті отримуємо
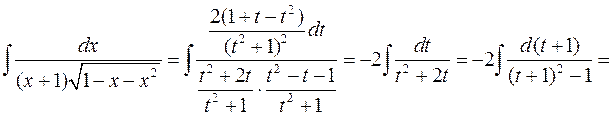
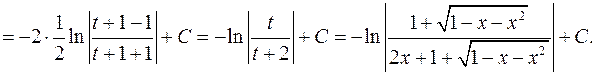
Підстановки Ейлера завжди дозволяють раціоналізувати інтеграли вигляду 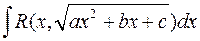 , але застосування цих підстановок часто пов’язане з дуже громіздкими обчисленнями. Досить часто менш трудомістким виявляється обчислення таких інтегралів за допомогою так званих тригонометричних підстановок. При цому інтеграл
, але застосування цих підстановок часто пов’язане з дуже громіздкими обчисленнями. Досить часто менш трудомістким виявляється обчислення таких інтегралів за допомогою так званих тригонометричних підстановок. При цому інтеграл 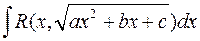 спочатку підстановкою
спочатку підстановкою 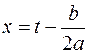 (вилученням повного квадрата в підкорінному виразі) зводиться до одного з таких інтегралів:
(вилученням повного квадрата в підкорінному виразі) зводиться до одного з таких інтегралів:
а) 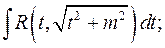 б)
б)  в)
в) 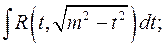 ,
,
a ці інтеграли перетворюються в інтеграли вигляду 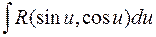 підстановками відповідно а)
підстановками відповідно а) 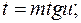 ; б)
; б) 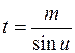 ; в)
; в) 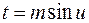 .
.
Про обчислення інтегралів 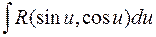 йтиме мова далі.
йтиме мова далі.
Date: 2015-09-02; view: 977; Нарушение авторских прав