
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Первісна функція. Невизначений інтеграл та його властивості
|
|
Інтегральне числення функцій однієї змінної
(конспект лекцій)

Первісна функція. Невизначений інтеграл та його властивості
В диференціальному численні основним завданням було відшукання похідної заданої функції. Але в багатьох питаннях математичного аналізу і його застосувань виникає потреба розв’язати обернену задачу: За даною функцією  знайти таку функцію
знайти таку функцію 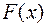 , похідна якої дорівнювала б
, похідна якої дорівнювала б  , тобто
, тобто 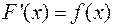 .
.
Приклад. У диференціальному численні було показано, що миттєва швидкість прямолінійного руху точки дорівнює похідній координати точки:  . Але якщо за заданою швидкістю руху точки
. Але якщо за заданою швидкістю руху точки 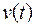 потрібно визначити закон її руху, тобто залежність її координати від часу
потрібно визначити закон її руху, тобто залежність її координати від часу  , то це і означає, що треба знайти таку функцію
, то це і означає, що треба знайти таку функцію  , похідна якої дорівнює заданій функції
, похідна якої дорівнює заданій функції 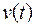 .
. 
Означення. Функція 
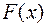 називається первісною для функції
називається первісною для функції  на деякому проміжку
на деякому проміжку 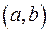 , якщо для всіх значень
, якщо для всіх значень 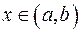 виконується рівність
виконується рівність 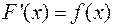 .
.
Приклад. Функція 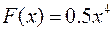 є первісною для функції
є первісною для функції  на всій числовій осі, бо при будь-якому значенні
на всій числовій осі, бо при будь-якому значенні 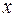 буде
буде 
 .
.
Зазначимо, що функції 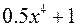 ,
,  і взагалі
і взагалі 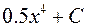 , де
, де 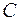 будь-яка стала, також є первісними для
будь-яка стала, також є первісними для  .
.
Розглянутий приклад свідчить, що первісна 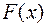 для даної функції
для даної функції 
 визначається неоднозначно. Справді, очевидно, що якщо
визначається неоднозначно. Справді, очевидно, що якщо 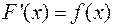 , то і
, то і 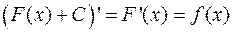 , тобто
, тобто 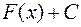 при будь-якій сталій
при будь-якій сталій 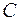 також є первісною для функції
також є первісною для функції  . Виникає питання: чи вичерпує множина функцій вигляду
. Виникає питання: чи вичерпує множина функцій вигляду 
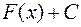 усю сукупність первісних для функції
усю сукупність первісних для функції  ? Виявляється, що так.
? Виявляється, що так.
Теорема. Якщо 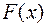 - первісна для функції
- первісна для функції  на деякому проміжку
на деякому проміжку 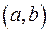 , то будь-яка інша первісна для
, то будь-яка інша первісна для  на тому ж проміжку може буди подана у вигляді
на тому ж проміжку може буди подана у вигляді 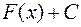 , де
, де 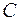 – стала.
– стала.
Нехай  - яка небудь інша первісна для
- яка небудь інша первісна для  на
на 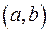 , тобто
, тобто  ,
, 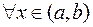 . Позначимо
. Позначимо  . Тоді для будь-якого
. Тоді для будь-якого  :
:
 .
.
Як відомо з диференціального числення, це означає, що  , отже
, отже 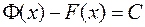 або
або 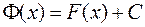 .
.
Означення. Множина всіх первісних для даної функції  на проміжку
на проміжку 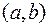 називається невизначеним інтегралом від функції
називається невизначеним інтегралом від функції  на цьому проміжку і позначається
на цьому проміжку і позначається 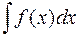 (
( називається підінтегральною функцією,
називається підінтегральною функцією, 
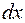 - підінтегральним виразом, а
- підінтегральним виразом, а 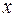 - змінною інтегрування).
- змінною інтегрування).
Згідно з вищезазначеним 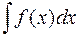 =
= 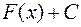 , де
, де 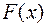 - яка небудь первісна для функції
- яка небудь первісна для функції  , а
, а 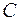 – довільна стала.
– довільна стала.
Відзначимо основні властивості невизначеного інтеграла.
1) Похідна невизначеного інтеграла дорівнює підінтегральній функції: 
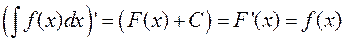 .
.
2) Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу: 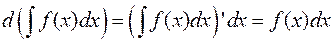 .
.
3) Невизначений інтеграл від диференціала деякої функції дорівнює сумі цієї функції і довільної сталої: 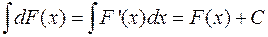 .
.
Перелічені властивості показують, що інтегрування і диференціювання
– взаємно обернені операції.
4) Сталий множник можна виносити за знак інтеграла: 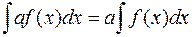 , якщо
, якщо  .
.
5) Невизначений інтеграл від алгебраїчної суми скінченного числа функцій дорівнює алгебраїчній сумі інтегралів від доданків. Наприклад 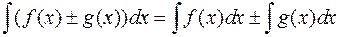 .
.
Властивості 4) і 5) перевіряються почленним диференціюванням відповідних рівностей на підставі 1).
Таблиця інтегралів
У наведеній нижче таблиці основних інтегралів частина формул безпосередньо випливає з таблиці похідних і визначення інтегрування як дії, оберненої до диференціювання, інші перевіряються диференціюванням. Цю таблицю необхідно вивчити, оскільки існуючі методи інтегрування якраз мають метою звести шуканий інтеграл до табличних.
1)  ,
, 
2) 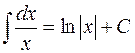 ,
,
3)  , зокрема
, зокрема  ,
,
4)  ,
,
5) 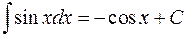 ,
,
6) 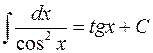 ,
,
7) 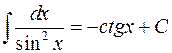 ,
,
8) 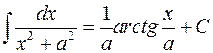 ,
,
9) 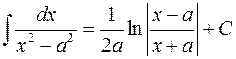 ,
,
10)  ,
,
11) 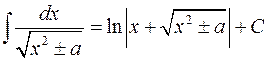 .
.
Основні властивості невизначеного інтеграла разом з наведеною тут таблицею інтегралів уже дозволяють знаходити деякі інтеграли (метод безпосереднього інтегрування).
Приклад. Знайти інтеграли
а)  .
.
б) 
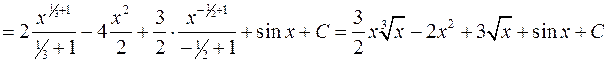 .
.
3. Заміна змінної в невизначеному інтегралі (метод підстановки)
Суть цього методу полягає в переході до нової змінної інтегрування з метою привести заданий інтеграл до «табличного вигляду», тобто до вигляду, що уможливлює безпосереднє інтегрування.
Теорема. Якщо 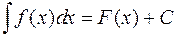 , а
, а  - диференційовна функція, то
- диференційовна функція, то
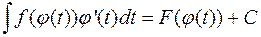 .
.
Справді, 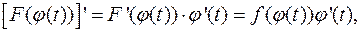 тобто
тобто 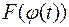 є первісною для
є первісною для 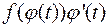 .
.
Таким чином будь-яка формула інтегрування зберігає силу, якщо в ній змінну інтегрування замінити диференційовною функцією від нової змінної. Зазвичай дана теорема використовується одним з двох способів:
1) Заданий інтеграл намагаються подати у вигляді 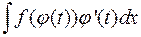 , де для функції
, де для функції  відома первісна
відома первісна 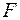 , тоді
, тоді 
 . Цей спосіб називають «впровадження під знак диференціала»:
. Цей спосіб називають «впровадження під знак диференціала»: 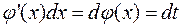 .
.
Приклад. Знайти інтеграл
 .
.
г) Заданий інтеграл 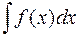 подають у вигляді
подають у вигляді 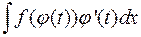 , де функція
, де функція 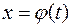 має обернену
має обернену  і для функції
і для функції  відома первісна
відома первісна 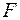 . Тоді
. Тоді
 .
.
Цей спосіб можна назвати «виведення з під знака диференціала»: 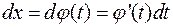 .
.
Приклад. Знайти інтеграл
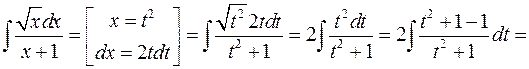
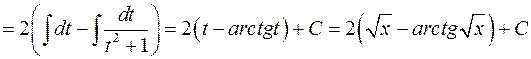
Date: 2015-09-02; view: 837; Нарушение авторских прав