Построения ее графика

Для качественного исследования графика функции y=f (x)

целесообразно провести следующие исследования:

1. Найти область определения функции.

2. Выяснить вопрос о существовании асимптот (вертикальных и наклонных).

3. Найти области возрастания и убывания функции и точки экстремума.

4. Найти области сохранения направления выпуклости и точки перегиба графика.

5. Найти точки пересечения с осью Оx.

Обычно по полученным данным легко строится эскиз графика.

В качестве примера построим график функции

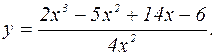
1. Наша функция представляет собой рациональную дробь. Она определена при всех значениях х, при которых знаменатель не обращается в нуль. Область определения функции 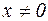(определена везде кроме точки х=0).

2. Выясним, есть ли асимптоты.

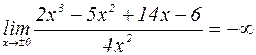
Таким образом, имеется вертикальная асимптота х=0.

А есть ли наклонная асимптота?

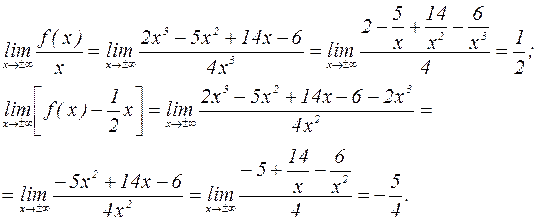
Итак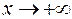, при и при 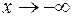график имеет наклонную асимптоту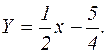

3. Для нахождения области возрастания и убывания вычислим первую производную

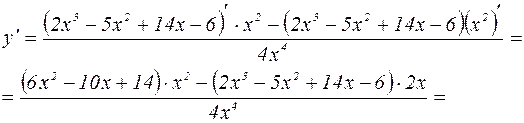
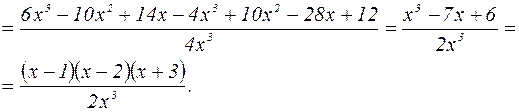
Имея в виду, что при х=0 функция и ее первая производная не существуют, составим таблицу, в которой отразим области сохранения знака первой производной

Область значений х
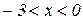
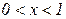
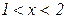
Знак	+	–	+	–	+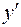
Поведение функции	Возр.	Убыв.	Возр.	Убыв.	Возр.

Из приведенной таблицы очевидно, что функция имеет следующие точки экстремума:

1) максимум при х= –3, при этом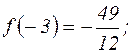

2) максимум при х=1,

3) минимум при х=2,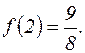

4. Для нахождения областей сохранения выпуклости вычислим вторую производную

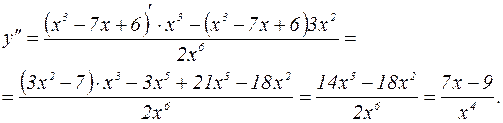
Составим таблицу сохранения знака 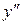(заметим, что при х=0 не существует).

Область значений х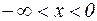
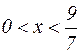
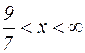
Знак	–	–	+
Направление выпуклости графика	Вверх	Вверх	Вниз

Из этой таблицы очевидно, что график функции имеет перегиб в точке 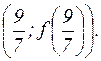При этом

5. Найдем точки пересечения графика с осью Оx. Эти точки соответствуют вещественным корням уравнения

(*)

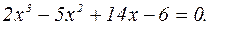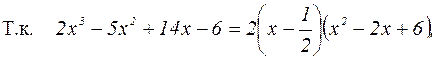а квадратный трехчлен имеет только комплексные корни

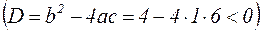, то уравнение (*) имеет единственный вещественный корень , т.е. график пересекает ось Оx только в точке . По полученным данным строим эскиз графика.

Date: 2015-09-02; view: 442; Нарушение авторских прав