
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные теоремы о пределах
|
|
Теорема 1.
Сходящаяся последовательность имеет только один предел.
Доказательство:
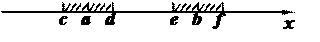 |
Предположим, что сходящаяся последовательность 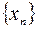 имеет два предела a и b. Выберем возле точек a и b на числовой оси интервалы (c, d) и (e, f), настолько малые, чтобы они не пересекались. Теперь воспользуемся третьим определением предела: если число a является пределом
имеет два предела a и b. Выберем возле точек a и b на числовой оси интервалы (c, d) и (e, f), настолько малые, чтобы они не пересекались. Теперь воспользуемся третьим определением предела: если число a является пределом 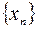 , то вне интервала (c, d) имеется только ограниченное число членов последовательности. Но это означает, что интервал (e, f) не может содержать бесконечное число членов последовательности
, то вне интервала (c, d) имеется только ограниченное число членов последовательности. Но это означает, что интервал (e, f) не может содержать бесконечное число членов последовательности 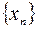 . Это противоречие доказывает, что сходящаяся последовательность может иметь только один предел. Теорема доказана.
. Это противоречие доказывает, что сходящаяся последовательность может иметь только один предел. Теорема доказана.
Теорема 2.
Сходящаяся последовательность ограничена.
Доказательство:
Пусть  . Тогда
. Тогда 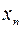 можно представить в виде
можно представить в виде 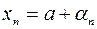 , где
, где 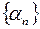 – бесконечно малая последовательность. Но бесконечно малая последовательность ограничена, т.е. найдется A>0, такое, что
– бесконечно малая последовательность. Но бесконечно малая последовательность ограничена, т.е. найдется A>0, такое, что  при всех n. Тогда
при всех n. Тогда 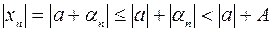 . Это неравенство выполняется для всех n, а это означает ограниченность последовательности
. Это неравенство выполняется для всех n, а это означает ограниченность последовательности 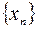 . Теорема доказана.
. Теорема доказана.
Еще несколько теорем о пределах. Пусть даны две сходящихся последовательности 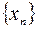 и
и 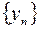 .
.
Значения 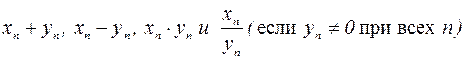 определяют последовательности
определяют последовательности 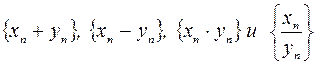 . Справедливы равенства:
. Справедливы равенства:
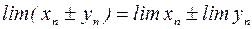 ; (1)
; (1)
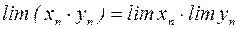 ; (2)
; (2)
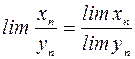 , если
, если 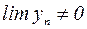 . (3)
. (3)
Эти формулы фактически задают арифметические действия с переменными, имеющими предел.
Доказательство равенства (1):
Пусть  Выберем
Выберем 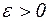 и подберем N так, чтобы при
и подберем N так, чтобы при 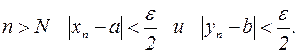 Тогда при
Тогда при 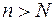
 Равенство доказано.
Равенство доказано.
Доказательство равенства (2):
Представим 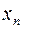 и
и 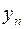 в виде:
в виде: 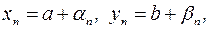 где
где 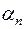 и
и 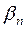 – члены бесконечно малых последовательностей. Тогда
– члены бесконечно малых последовательностей. Тогда 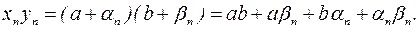 Поэтому
Поэтому 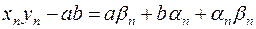 . При этом последовательность
. При этом последовательность 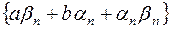 – бесконечно малая последовательность, т.к. бесконечно малой последовательностью является каждая из трех переменных
– бесконечно малая последовательность, т.к. бесконечно малой последовательностью является каждая из трех переменных 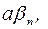
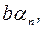
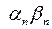 . Поэтому последовательность
. Поэтому последовательность 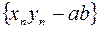 также бесконечно малая, а последовательность
также бесконечно малая, а последовательность 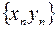 сходится и ab – ее предел. Равенство доказано.
сходится и ab – ее предел. Равенство доказано.
Для доказательства равенства (3) сначала докажем лемму.
Лемма.
Если последовательность 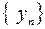 сходится и имеет отличный от нуля предел b, то, начиная с некоторого номера, определена последовательность
сходится и имеет отличный от нуля предел b, то, начиная с некоторого номера, определена последовательность 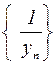 , которая является ограниченной.
, которая является ограниченной.
Доказательство:
Пусть 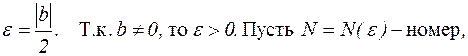 начиная с которого выполняется неравенство
начиная с которого выполняется неравенство 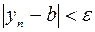 или
или 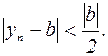 Тогда
Тогда 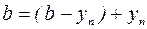 ,
, 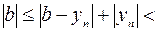
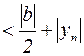 , т.е.
, т.е. 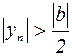 . Поэтому при
. Поэтому при 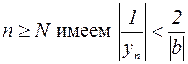 . Следовательно, начиная с этого N мы можем рассматривать последовательность
. Следовательно, начиная с этого N мы можем рассматривать последовательность 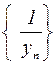 и она ограничена. Лемма доказана.
и она ограничена. Лемма доказана.
Доказательство равенства (3):
Если 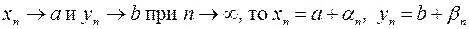 , где
, где 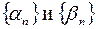 – бесконечно малые последовательности. Тогда
– бесконечно малые последовательности. Тогда


Таким образом  Равенство (3) доказано.
Равенство (3) доказано.
Итак, мы выяснили, что арифметические операции над сходящимися последовательностями приводят к таким же операциям над их пределами. Этот очень важный вывод поможет вычислять пределы различных последовательностей.
Оказывается, что если элементы (члены) сходящихся последовательностей удовлетворяют некоторым неравенствам, то таким же неравенствам удовлетворяют и пределы их последовательностей.
Теорема.
Если элементы сходящейся последовательности 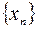 , начиная с некоторого номера, удовлетворяют неравенству
, начиная с некоторого номера, удовлетворяют неравенству  , то и предел a этой последовательности удовлетворяет неравенству
, то и предел a этой последовательности удовлетворяет неравенству  .
.
Доказательство:
Пусть начиная с некоторого номера все элементы 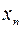 удовлетворяют неравенству
удовлетворяют неравенству 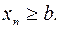 Требуется доказать, что
Требуется доказать, что 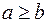 . Предположим противное, т.е. что
. Предположим противное, т.е. что 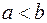 . Введем
. Введем 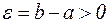 . Для этого
. Для этого 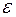 существует номер
существует номер  такой, что при
такой, что при 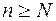
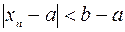 или
или 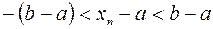 . Из правого неравенства тогда следует, что
. Из правого неравенства тогда следует, что 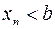 , а это противоречит условию теоремы. Случай
, а это противоречит условию теоремы. Случай  рассматривается аналогично. Теорема доказана.
рассматривается аналогично. Теорема доказана.
Следствие 1.
Если элементы 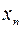 и
и 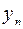 сходящихся последовательностей, начиная с некоторого номера, удовлетворяют неравенству
сходящихся последовательностей, начиная с некоторого номера, удовлетворяют неравенству 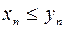 , то и их пределы удовлетворяют такому же неравенству
, то и их пределы удовлетворяют такому же неравенству 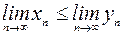 .
.
Следствие 2.
Если все элементы сходящейся последовательности 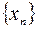 находятся на отрезке
находятся на отрезке 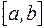 , то и ее предел С также находится на этом отрезке.
, то и ее предел С также находится на этом отрезке.
Теорема.
Пусть 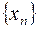 и
и  – сходящиеся последовательности, имеющие общий предел a. Пусть, кроме того, начиная с некоторого номера, элементы последовательности
– сходящиеся последовательности, имеющие общий предел a. Пусть, кроме того, начиная с некоторого номера, элементы последовательности 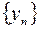 удовлетворяют неравенствам
удовлетворяют неравенствам 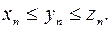 Тогда последовательность
Тогда последовательность 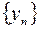 сходится и имеет предел a.
сходится и имеет предел a.
Доказательство:
Пусть N* – номер, начиная с которого выполняются неравенства 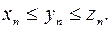 Тогда с этого же номера выполняются неравенства
Тогда с этого же номера выполняются неравенства 
Очевидно, что при 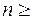 N*
N* 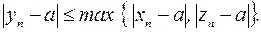
Т.к. 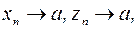 то для любого
то для любого 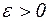 можно указать номера N1 и N2 такие, что при
можно указать номера N1 и N2 такие, что при 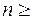 N1
N1 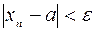 , а при
, а при 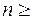 N2
N2 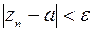 .
.
Пусть 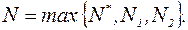 Очевидно, при
Очевидно, при 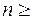 N
N 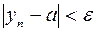 , т.е. последовательность
, т.е. последовательность 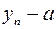 – бесконечно малая последовательность. Теорема доказана.
– бесконечно малая последовательность. Теорема доказана.
Date: 2015-09-02; view: 456; Нарушение авторских прав