
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Бесконечно малые и бесконечно большие последо-
|
|
вательности
Определение.
Последовательность 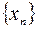 называется бесконечно большой, если для любого А>0 можно указать номер
называется бесконечно большой, если для любого А>0 можно указать номер  такой, что при
такой, что при 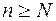 все члены xn этой последовательности удовлетворяют неравенству
все члены xn этой последовательности удовлетворяют неравенству 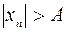 .
.
Замечание.
Любая бесконечно большая последовательность является неограниченной; однако неограниченная последовательность может и не быть бесконечно большой. Пример: последовательность 1, 2, 1, 3, …, 1, n,... является неограниченной, но не является бесконечно большой, т.к. при A>1 неравенство 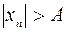 не имеет места для всех членов xn с нечетными номерами.
не имеет места для всех членов xn с нечетными номерами.
Определение.
Последовательность  называется бесконечно малой, если для любого
называется бесконечно малой, если для любого 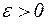 можно указать номер
можно указать номер 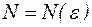 такой, что при
такой, что при 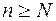 все члены
все члены 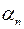 этой последовательности удовлетворяют неравенству
этой последовательности удовлетворяют неравенству 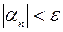 .
.
Примеры:
1) Доказать, что последовательность 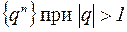 является бесконечно большой, а при
является бесконечно большой, а при 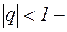 бесконечно малой.
бесконечно малой.
а) Пусть  . Тогда
. Тогда  , где
, где 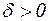 .
.
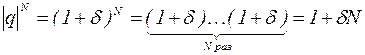 +(положительные члены), т.е.
+(положительные члены), т.е. 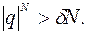 Теперь зафиксируем произвольное число A>0 и выберем N столь большим, чтобы
Теперь зафиксируем произвольное число A>0 и выберем N столь большим, чтобы 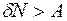 (например, выберем
(например, выберем  ). Тогда
). Тогда 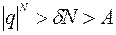 . Но при
. Но при  и
и 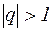
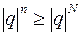 ,т.е.
,т.е.  Утверждение доказано.
Утверждение доказано.
б) Пусть 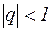 . В этом случае
. В этом случае 
Теперь
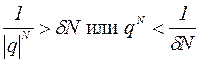 . Зафиксируем произвольное
. Зафиксируем произвольное 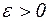 и выберем номер N из условия
и выберем номер N из условия 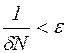 . Т.к.
. Т.к. 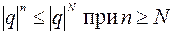 и при
и при 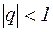 , то из полученных неравенств вытекает, что
, то из полученных неравенств вытекает, что 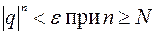 . Утверждение доказано.
. Утверждение доказано.
2) Докажем, что 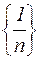 – бесконечно малая последовательность. В самом деле, если
– бесконечно малая последовательность. В самом деле, если 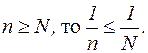 Поэтому по заданному
Поэтому по заданному 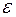 достаточно выбрать номер N из условия
достаточно выбрать номер N из условия 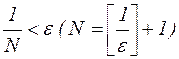 . Тогда при
. Тогда при 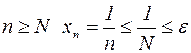 и утверждение доказано.
и утверждение доказано.
Теорема.
Если 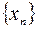 – сходящаяся последовательность и
– сходящаяся последовательность и 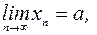 то
то 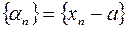 – бесконечно малая последовательность.
– бесконечно малая последовательность.
Доказательство:
Т.к. для любого 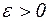 можно найти номер
можно найти номер  такой, что при
такой, что при 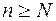 выполняется неравенство
выполняется неравенство 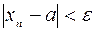 , это и означает, что при
, это и означает, что при 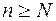
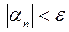 , т.е.
, т.е. 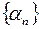 – бесконечно малая последовательность.
– бесконечно малая последовательность.
Из этой теоремы следует, что члены сходящейся последовательности 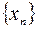 могут быть представлены в виде:
могут быть представлены в виде:

где  – бесконечно малая последователь-ность.
– бесконечно малая последователь-ность.
Date: 2015-09-02; view: 444; Нарушение авторских прав