Монотонные последовательности

Определение.

Последовательность 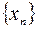называется неубывающей (невозрастающей), если для всех n справедливо неравенство .

Если выполняются строгие неравенства 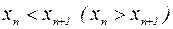, то последовательность называется возрастающей (убывающей). Убывающие, возрастающие, неубывающие и невозрастающие последовательности называются монотонными.

Монотонные последовательности ограничены либо сверху, либо снизу. А именно: невозрастающая последовательность ограничена сверху (своим первым элементом x₁), а неубывающая последовательность ограничена снизу (также элементом x₁).

Если же невозрастающая последовательность ограничена еще и снизу, то она является ограниченной с двух сторон. Точно так же неубывающая последовательность, ограниченная сверху, ограничена с двух сторон.

Теорема.

Если неубывающая (невозрастающая) последовательность 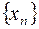ограничена сверху (снизу) числом M(m), то она имеет предел a, причем .

С учетом только что сделанных замечаний эту теорему можно сформулировать так: если монотонная последовательность ограничена с обеих сторон, то она сходится.

Доказательство:

Ограничимся доказательством для неубывающей последовательности 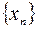. Докажем, что пределом такой последовательности является точная верхняя грань .

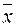Поскольку 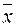– точная верхняя грань множества элементов последовательности 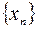, то для любого 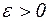можем указать элемент x_N такой, что и 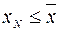. Сопоставим эти неравенства и получим . Т.к. 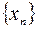– неубывающая последовательность, то при 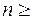N 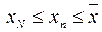. Таким образом, при 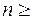N выполняются неравенства 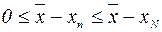и так как 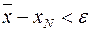, то эти неравенства записываются в виде 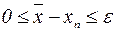, т.е. . Итак, доказано, что число 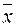– предел последовательности .

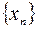Замечание.

Отметим, что для монотонных последовательностей ее элементы приближаются к пределу с одной стороны. Так, для неубывающей последовательности 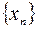, пределом которой является 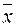, для всех n справедливо неравенство 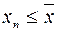. Для немонотонных последовательностей возможно приближение к пределу с обеих сторон. Пример мы уже имели:

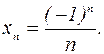
Очевидно, 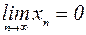, но знаки элементов этой последовательности чередуются.

Следствие из теоремы (принцип вложенных отрезков).

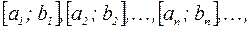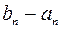Пусть дана бесконечная система отрезков каждый следующий из которых содержится в предыдущем, т.е. . Пусть разность (длина отрезка ) стремится к нулю при .

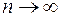Тогда существует, и притом единственная точка С, принадлежащая всем отрезкам этой системы.

Доказательство:

Очевидно, последовательность левых концов отрезков является неубывающей, а последовательность 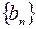правых концов – невозрастающая. Поскольку обе эти последовательности ограничены (все элементы последовательностей и 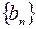находятся на отрезке 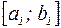), то обе они сходятся.

Из того, что разность 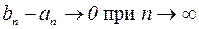вытекает, что обе эти последовательности имеют общий предел С. Тогда ясно, что 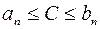, т.е. точка С принадлежит всем сегментам . Утверждение доказано.

Число e.

Прежде, чем дать определение числа e (основания натуральных логарифмов), играющего важную роль в математике, напомню вам формулу бинома Ньютона. Речь идет о возведении двучлена (a+b) в любую натуральную степень n.

Если n=1, то ;

n=2, то ;

n=3, то ;

Т.к. 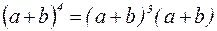, можно получить формулу .

В общем случае справедлива формула, носящая название бинома Ньютона:

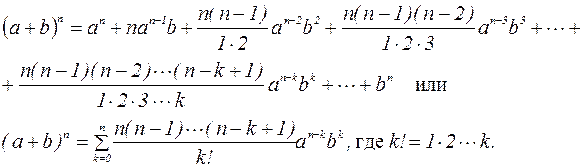
Рассмотрим последовательность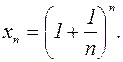

На основании формулы бинома Ньютона:

Отсюда видно, что все члены положительны, так что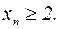

С другой стороны, заменив каждую скобку единицей, мы увеличим это выражение так, что:

.

Теперь заметим, что

т.е. 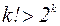при .

Если все знаменатели заменить на 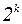, то правая часть только возрастет.

Таким образом,

Таким образом, при всех n.

Теперь покажем, что 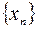– возрастающая последовательность.

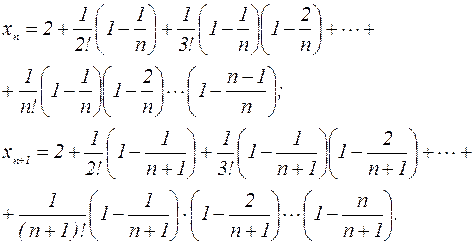
Сравнивая эти выражения, заметим, что в выражении для 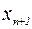на одно положительное слагаемое больше, чем в выражении для . Кроме того, во вторых слагаемых в третьих слагаемых

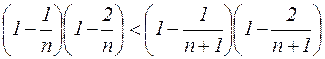и т.д..

Таким образом, каждое слагаемое в меньше соответствующего слагаемого в 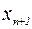. Итак, , т.е. последовательность 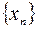– возрастающая. Поскольку она ограниченная, следовательно, сходится к некоторому пределу e, причем e – иррациональное число, – выражается бесконечной не-периодической дробью.

Таким образом, .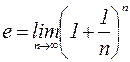

Date: 2015-09-02; view: 417; Нарушение авторских прав