
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифференциальное исчисление
|
|
Лекция № 18. Тема 4: Производная и дифференциал
4.1. Производная функции
Пусть функция  определена в точке х и некоторой её окрест-ности
определена в точке х и некоторой её окрест-ности 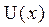 .
.
Определение 1. Производной от функции  в точке х называется предел отношения её приращения
в точке х называется предел отношения её приращения 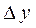 в этой точке к соответствующему приращению аргумента
в этой точке к соответствующему приращению аргумента 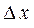 при
при  и обозначается
и обозначается
.  (1)
(1)
Другие обозначения производной: 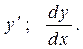
Замечание 1. Очевидно для существования предела (1) необходимо вы-полнение равенства  , где
, где 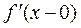 - левая производ-ная (
- левая производ-ная (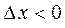 ), а
), а 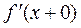 - правая производная (
- правая производная (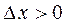 ).
).
Определение 2. Функция  , имеющая конечную производную в точке х, называется дифференцируемой в этой точке, а если она диффе-ренцируемая в каждой точке промежутка
, имеющая конечную производную в точке х, называется дифференцируемой в этой точке, а если она диффе-ренцируемая в каждой точке промежутка 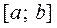 , то она называется диффе-ренцируемой в этом промежутке.
, то она называется диффе-ренцируемой в этом промежутке.
Замечание 2. Не для всех функций существует предел (1).
Например, определим производную функции  в точке
в точке  раскроем знак модуля, вычисляя предел (1) слева и справа,
раскроем знак модуля, вычисляя предел (1) слева и справа,
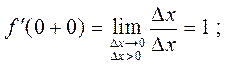
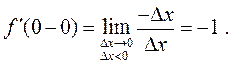
Таким образом, функция  является не дифференцируемой в точке
является не дифференцируемой в точке 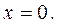
Пример показывает, что не всякая непрерывная функция является дифференцируемой. Верно ли обратное?
Теорема 1. Если функция 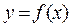 дифференцируемая в некоторой точке x, то она в этой точке непрерывна.
дифференцируемая в некоторой точке x, то она в этой точке непрерывна.
Пусть существует предел (1). Это по теореме о пределе функции означает, что
 , где
, где 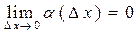 . (2)
. (2)
Из формулы (2) следует 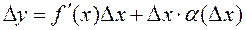 . Переходя к пределу, получаем
. Переходя к пределу, получаем
 , ч.т.д.
, ч.т.д.
Обратное, вообще говоря, неверно (например, функция  ).
).
4.2. Производные основных элементарных функций
Используя определение производной, можно получить значения производных основных элементарных функций. Рассмотрим примеры:
Пример 1. Найти производную функцию 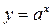 .
.
 .
.
В частности, если 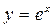 , то
, то  .
.
Пример 2. Аналогично, для функции 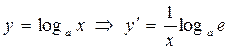 .
.
В частности, если 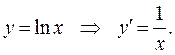
Пример 3. Найти производную функции 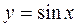 .
.
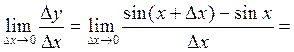
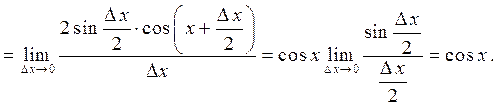
Пример 4. Аналогично, для функции 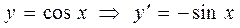 .
.
Приведём таблицу производных элементарных функций:
1. 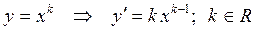 .
.
2.  . 3.
. 3.  .
.
4.  . 5.
. 5. 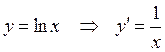 .
.
6. 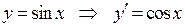 . 7.
. 7.  .
.
8.  . 9.
. 9. 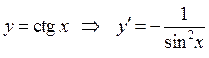 .
.
10.  . 11.
. 11. 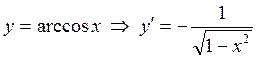 .
.
12. 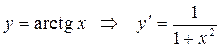 . 13.
. 13. 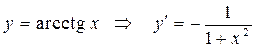 .
.
Формулы (2-7) нами доказаны.
Остальные формулы будут доказаны позже.
4.3. Механический смысл производной
Рассмотрим прямолинейное движение точки М. Пусть в момент времени t точка М находится на расстоянии 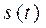 от начального поло-жения М 0.
от начального поло-жения М 0.
t 0 t 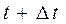



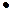
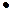
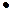 s
s
М 0 М М 1
В последующий момент 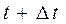 точка М заняла положение М 1 на расстоянии
точка М заняла положение М 1 на расстоянии 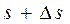 от начального положения. Тогда средняя скорость за
от начального положения. Тогда средняя скорость за 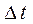 будет
будет 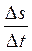 , а скорость
, а скорость 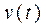 в момент времени t:
в момент времени t:
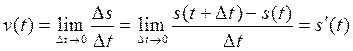 .
.
Таким образом, если функция 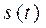 – это путь, проходимый точкой М, то производная
– это путь, проходимый точкой М, то производная 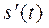 от этой функции – скорость
от этой функции – скорость 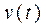 движения точки.
движения точки.
4.4. Геометрический смысл производной
 Пусть функция дифференцируема в точке х.
Пусть функция дифференцируема в точке х.
у 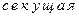
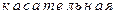
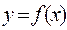
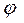
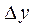
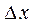
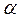
О х 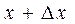 х
х
Из рисунка следует, что 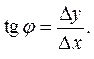 Перейдём к пределу при
Перейдём к пределу при 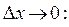
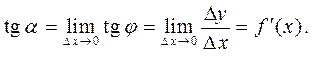
Таким образом, значение производной равно тангенсу угла наклона касательной, проведённой в данной точке. Исходя из этого, уравнение касательной в точке 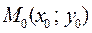 к кривой
к кривой 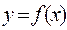 имеет вид
имеет вид
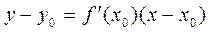 .
.
Прямая, проходящая через точку М 0, перпендикулярно касательной называется нормалью. Её уравнение имеет вид
 .
.
Отметим частный случай:
если 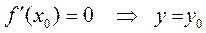 - уравнение касательной,
- уравнение касательной, 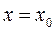 - нормали.
- нормали.
Пример 6. Найти уравнения касательной и нормали к функции 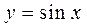 в точке
в точке 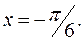
Имеем 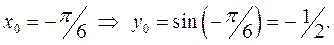
Найдем производную функции 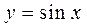
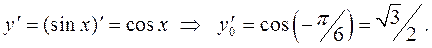
Таким образом, получим
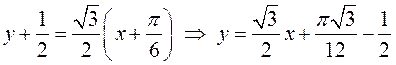 - уравнение касательной,
- уравнение касательной,
 - уравнение нормали.
- уравнение нормали.
4.5. Правила дифференцирования
Пусть функции U и V дифференцируемые.
1. Если  .
.
2. 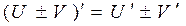 .
.
3. 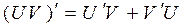 .
.
4. 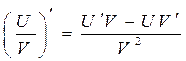 .
.
Докажем последнее правило
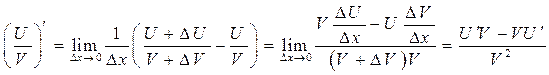 .
.
Пример 5. Найти производные функций 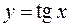 и
и 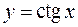
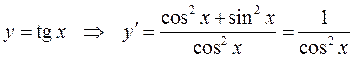 .
.
Аналогично,
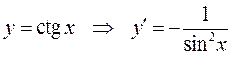 ,
,
т.е. доказаны формулы (8-9) таблицы производных.
4.6. Производная сложной функции
Пусть дана сложная функция  , т.е.
, т.е. 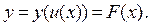
Теорема 2. Если функция 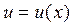 имеет в точке x производную
имеет в точке x производную 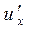 , а функция
, а функция 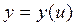 в соответствующей точке и также имеет производную
в соответствующей точке и также имеет производную  , то сложная функция
, то сложная функция 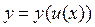 в точке х имеет производную, которая равна
в точке х имеет производную, которая равна
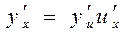 .
.
По условию теоремы существует  . По теореме о пре-деле функции из существования этого предела следует
. По теореме о пре-деле функции из существования этого предела следует
 ,
,
где 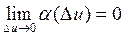 или
или
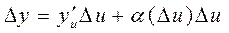 . (3)
. (3)
Разделим выражение (3) на 
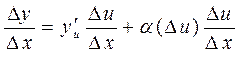 . (4)
. (4)
Переходя к пределу в формуле (4) при 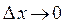 , а тогда в силу непрерывности и
, а тогда в силу непрерывности и 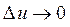 , получим
, получим
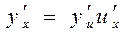 . (5)
. (5)
Замечание 3. Формулу (5) можно обобщить для любого числа суперпозиций функций. Например, если
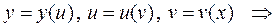
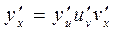 .
.
Пример 7. Найти  , если
, если 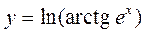 .
.
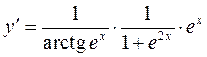 .
.
Пример 8. Найти  , если
, если 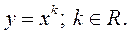
Представим  и по правилу дифференцирования сложной функции получим
и по правилу дифференцирования сложной функции получим
 ,
,
т.е. доказана и первая формула из таблицы производных.
Лекция № 19.
4.7. Производная обратной функции
Теорема. Пусть функция 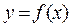 монотонна в некоторой окрестности точки х и
монотонна в некоторой окрестности точки х и 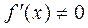 , тогда обратная функция
, тогда обратная функция 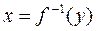 также имеет производную в соответствующей точке х, которая определяется по формуле
также имеет производную в соответствующей точке х, которая определяется по формуле
 . (1)
. (1)
Действительно, в силу монотонности функции 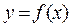 для приращения
для приращения 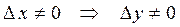 и тогда
и тогда
 . (2)
. (2)
Если  , то в силу непрерывности
, то в силу непрерывности 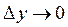 , и, переходя к пределу в выражении (2), получаем формулу (1).
, и, переходя к пределу в выражении (2), получаем формулу (1).
Пример 1. Найти 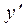 , если
, если 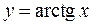 .
.
Обратная к этой функции есть функция 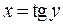 и тогда по формуле (1) получаем
и тогда по формуле (1) получаем
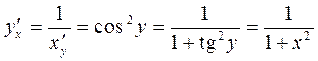 .
.
Для функции 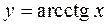 имеем
имеем
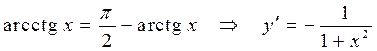 .
.
Аналогично можно доказать формулы (10-11) таблицы производных.
4.8. Производная функции, заданной параметрическими уравнениями
Пусть функция задана параметрическими уравнениями 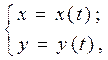
тогда справедлива следующая
Теорема. Если функции 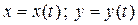 являются дифференцируемы-ми в соответствующей точке, то
являются дифференцируемы-ми в соответствующей точке, то
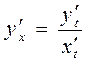 .
.
Пусть функция 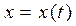 имеет обратную функцию
имеет обратную функцию 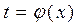 , тогда функция
, тогда функция 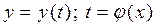 является сложной функцией и по правилу дифференцирования сложной функции (4.6) получаем
является сложной функцией и по правилу дифференцирования сложной функции (4.6) получаем 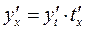 . Если воспользоваться формулой (1), то имеем
. Если воспользоваться формулой (1), то имеем
 .
.
Пример 2. Составить уравнение касательной к линии 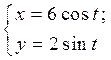 при
при 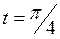 , т.е. в точке
, т.е. в точке  .
.
Имеем
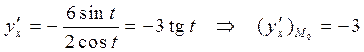 ,
,
тогда уравнение касательной
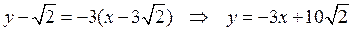 .
.
4.9. Производная функции, заданной неявно
Пусть функция задана неявно
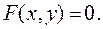 (3)
(3)
Продифференцируем выражение (3) по аргументу х с учётом, что 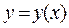 и разрешим полученное соотношение относительно
и разрешим полученное соотношение относительно 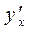 . Покажем эту процедуру на конкретном примере.
. Покажем эту процедуру на конкретном примере.
Пример 3. Найти 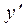 , если
, если  .
.
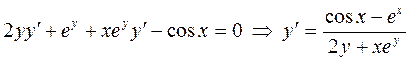 .
.
4.10. Производная степенно-показательной функции
Определение 1. Функция вида 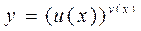 называется степенно-показательной.
называется степенно-показательной.
Прологарифмируем эту функцию
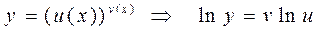 . (4)
. (4)
Дифференцируя обе части выражения (4), получим

или
 (5)
(5)
Рассмотренная операция называется логарифмическим дифференциро-ванием. Формулу (5) можно удобно запомнить как сумму производных от показательной и степенной функций.
Пример 4. Найти 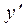 , если
, если 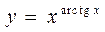 .
.
Прологарифмируем  .
.
Дифференцируя полученное равенство, окончательно имеем
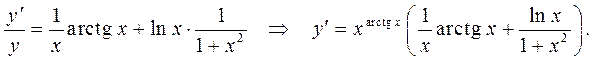
4.11. Производные высших порядков
Если функция  дифференцируема, то функция
дифференцируема, то функция 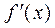 называется производной первого порядка и может также быть дифференцируемой функцией, тогда производная от этой функции называется второй производной от функции
называется производной первого порядка и может также быть дифференцируемой функцией, тогда производная от этой функции называется второй производной от функции  и обозначается
и обозначается
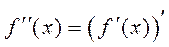 или
или 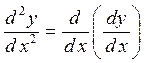 .
.
Вообще производной порядка п от функции  называется первая производная от производной ( п - 1)-го порядка и обозначается
называется первая производная от производной ( п - 1)-го порядка и обозначается
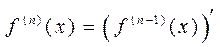 или
или  .
.
Пример 5. Найти п -ю производную от функции 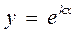 .
.
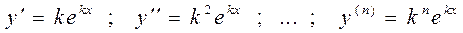 .
.
Пусть функция задана параметрическими уравнениями 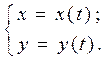
Тогда, как известно,
 .
.
Таким образом, в этом случае можно для нахождения 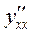 использовать следующие формулы:
использовать следующие формулы:
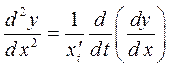 . (6)
. (6)
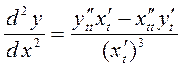 . (7)
. (7)
Формулу (6) удобно использовать, если перед этим уже найдена 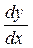 .
.
Пример 6. Найти 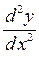 циклоиды
циклоиды 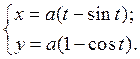
По формуле (7) получаем
 .
.
Нахождение второй производной функции, заданной неявно, рассмот-рим на примере
Пример 7. Найти 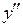 , если
, если 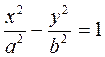 .
.
Продифференцируем это уравнение
 .
.
Продифференцируем найденную первую производную  ещё раз
ещё раз
 .
.
С учётом выражения для  и самой функции окончательно получим
и самой функции окончательно получим
 .
.
Замечание 1. Аналогично можно находить производные высших поряд-ков от функций, заданных неявно или параметрическими уравнениями.
Замечание 2. Как и для производной первого порядка, можно рас-смотреть механический смысл второй производной, а именно, если 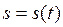 - путь, пройденный материальной точкой, то ускорение
- путь, пройденный материальной точкой, то ускорение  .
.
4.12. Дифференциал функции
Пусть функция 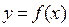 имеет в точке х производную, т.е. существует
имеет в точке х производную, т.е. существует
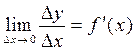 .
.
Тогда по теореме о пределе функции
 ,
,
где 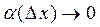 при
при  или
или
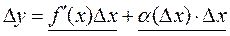 . (8)
. (8)
Второе слагаемое в формуле (8) является б.м.в. более высокого порядка, чем 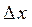 . Первое слагаемое называется главной или линейной частью приращения функции.
. Первое слагаемое называется главной или линейной частью приращения функции.
Определение 2. Главная часть приращения 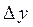 называется дифферен-циалом функции и обозначается
называется дифферен-циалом функции и обозначается
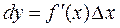 . (9)
. (9)
Тогда формула (8) примет вид
 .
.
В частности, для функции  , т.е. для аргу-мента
, т.е. для аргу-мента  и поэтому окончательно формула (9) принимает вид
и поэтому окончательно формула (9) принимает вид
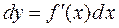 .
.
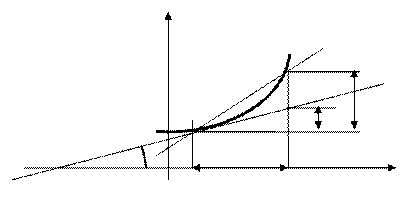 Из рисунка следует геомет- у
Из рисунка следует геомет- у
рический смысл дифференциала. 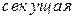
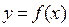
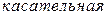
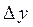
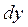
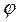
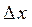 х
х
Таким образом, дифференциал функции 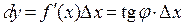 – это приращение ординаты точки, лежащей на касательной.
– это приращение ординаты точки, лежащей на касательной.
Отметим основные свойства дифференциала, которые следуют из соответствующих правил дифференцирования:
1. 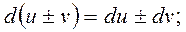
2. 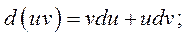
3. 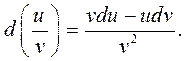
Найдём выражение для дифференциала сложной функции 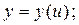
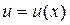 . Тогда
. Тогда  или
или  .
.
Таким образом, форма дифференциала не зависит от того, является ли аргумент функции независимой переменной или функцией другого аргу-мента. Это свойство первого дифференциала называется инвариантностью.
Замечание 3. Из обозначения производной 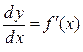 следует, что производную
следует, что производную 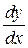 можно рассматривать как отношение дифференциалов.
можно рассматривать как отношение дифференциалов.
Лекция № 20.
Тема 5: Основные теоремы о дифференцируемых функциях
5.1. Теорема Ролля
Теорема. Если функция 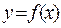 непрерывна на
непрерывна на  , дифференцируема на
, дифференцируема на 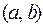 и
и 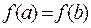 , то существует такая точка
, то существует такая точка 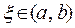 , что
, что 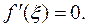
Если 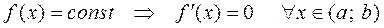 .
.
Поэтому будем считать, что 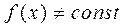 и в силу непрерывности функции
и в силу непрерывности функции  она достигает на
она достигает на 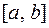 своего наибольшего и наименьшего значений. При этом, так как
своего наибольшего и наименьшего значений. При этом, так как 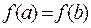 , то хотя бы одно из них дости-гается внутри промежутка
, то хотя бы одно из них дости-гается внутри промежутка 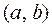 . Пусть это
. Пусть это  .
.
Покажем, что 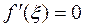 (теорема Ферма). При
(теорема Ферма). При 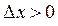 имеем
имеем
 .
.
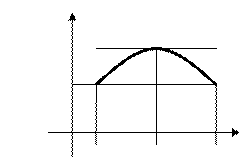 Аналогично, при
Аналогично, при 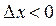
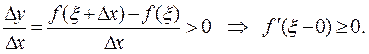
В силу дифференцируемости  имеем у
имеем у
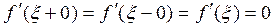 .
.
Замечание 1. Теорема имеет 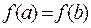
простой геометрический смысл:
существует точка 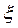 , в которой х
, в которой х
касательная к кривой 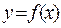 а
а 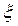 b
b
параллельна оси О х.
5.2. Теорема Лагранжа
Теорема. Если функция 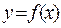 непрерывна на
непрерывна на 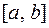 , дифференци-руема на
, дифференци-руема на 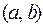 , то существует такая точка
, то существует такая точка 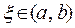 , в которой
, в которой
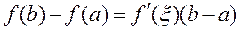 .
.
Составим функцию
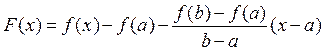 .
.
Так как функция 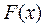 непрерывна на
непрерывна на 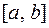 , дифференцируема на
, дифференцируема на 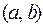 и
и 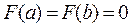 , то по теореме Ролля существует точка
, то по теореме Ролля существует точка 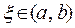 , в которой
, в которой 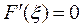 , т.е.
, т.е.
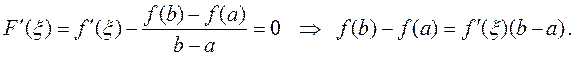
5.3. Правило Лопиталя
Теорема. (Раскрытие неопределённости вида 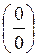 ). Пусть
). Пусть  и
и 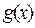 дифференцируемы в окрестности точки x 0 и
дифференцируемы в окрестности точки x 0 и 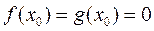 . Тогда, если существует
. Тогда, если существует 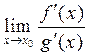 , то существует
, то существует 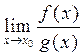 и
и  .
.
Запишем отношение функций 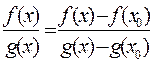 . К числителю и зна-менателю применим теорему Лагранжа
. К числителю и зна-менателю применим теорему Лагранжа 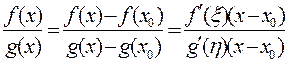 , где
, где 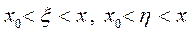 .
.
Если перейти к пределу при 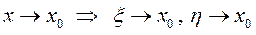 , тогда
, тогда
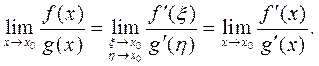
Замечание 2. Правило Лопиталя справедливо и для случая, если 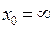 , так как заменой
, так как заменой  он сводится к случаю при
он сводится к случаю при 
Покажем это, 
 .
.
Замечание 3. Теорема имеет место и для неопределённости вида 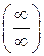 . Неопределенности видов
. Неопределенности видов 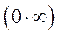 и
и 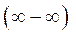 приводятся к рассмотренным
приводятся к рассмотренным
случаям путём алгебраических преобразований.
Например, с неопределённостью вида 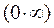 поступают следующим образом:
поступают следующим образом: 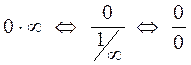 .
.
При неопределённостях вида:  применяют лога-рифмирование, т.е. вместо предела функции
применяют лога-рифмирование, т.е. вместо предела функции 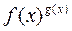 рассматривается предел
рассматривается предел
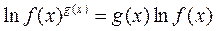 .
.
Замечание 4. Требование существования предела в правиле Лопиталя существенно. Так, например, правило Лопиталя нельзя применить к пределу
 , так как не существует
, так как не существует  . В тоже время
. В тоже время

Пример 1. 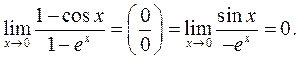
Пример 2. 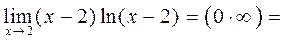
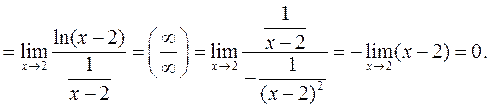
Пример 3. 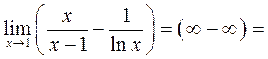
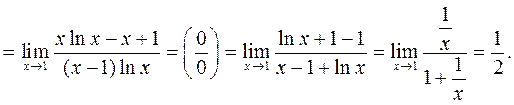
Пример 4. 
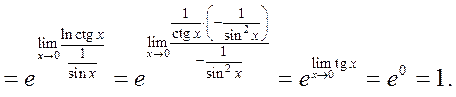
5.4. Формула Тейлора
Для функции  , которая имеет производные до (п + 1)-го порядка включительно в некоторой окрестности точки х 0, найдём многочлен сте-пени п, который удовлетворяет следующим условиям:
, которая имеет производные до (п + 1)-го порядка включительно в некоторой окрестности точки х 0, найдём многочлен сте-пени п, который удовлетворяет следующим условиям:
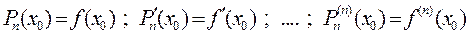 . (1)
. (1)
Будем его искать в виде
 . (2)
. (2)
Определим из условий (1) коэффициенты 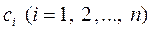 в выра-жении (2), дифференцируя его и подставляя значение
в выра-жении (2), дифференцируя его и подставляя значение 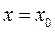 .
.
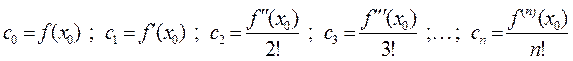 .
.
И тогда получим
 . (3)
. (3)
Естественно ожидать, что многочлен (3) в окрестности точки х 0 мало отличается от функции  . Обозначим разность
. Обозначим разность 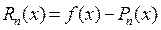 , которая называется остаточным членом.
, которая называется остаточным членом.
Остаточный член в форме Лагранжа имеет вид

где  . Если остаточный член мал, то имеем приближенную формулу
. Если остаточный член мал, то имеем приближенную формулу 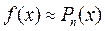 .
.
Пример 5. Составить формулу Тейлора для функции 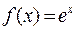 в окрест-ности точки
в окрест-ности точки  и вычислить с точностью
и вычислить с точностью 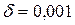 значение
значение 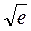 .
.
Учитывая, что  и
и 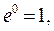 получим
получим
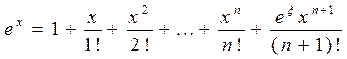 .
.
Положим в этой формуле
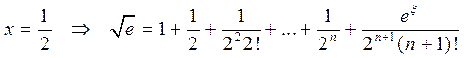 ,
,
где 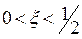 . Из оценки остаточного члена определим п, т.е. решим неравенство
. Из оценки остаточного члена определим п, т.е. решим неравенство
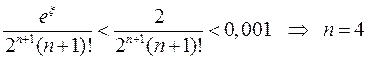
и тогда окончательно получим

Лекция № 21. Тема 6: Исследование поведения функций
6.1. Возрастание и убывание функций
Теорема. Если дифференцируемая на  функция
функция  возрастает (убывает), то
возрастает (убывает), то  выполняется
выполняется 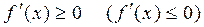 . Верно и обратное.
. Верно и обратное.
Пусть 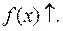 Тогда отношение
Тогда отношение 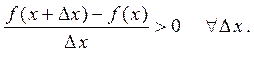
Переходя к пределу, получаем 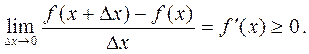
Аналогично доказывается случай 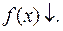
Докажем обратное утверждение. Пусть  , а
, а  . По теореме Лагранжа имеем
. По теореме Лагранжа имеем
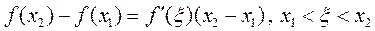 .
.
Отсюда, с учётом знака правой части, имеем 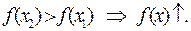
Аналогично доказывается случай 
Замечание 1. В некоторых точках может быть 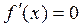 , так как производная является пределом.
, так как производная является пределом.
Пример 1. Найти интервалы возрастания и убывания функции

Находим производную заданной функции 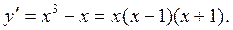
Знаки производной определим методом интервалов:
 |
- + - +

-1 0 1 х
Тогда имеем 
6.2. Экстремум функции. Необходимое условие
Определение 1. Точка х 0 называется точкой максимума (минимума) функции  , если в некоторой окрестности этой точки выполняется
, если в некоторой окрестности этой точки выполняется  .
.
Определение 2. Точки максимума 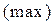 и точки минимума
и точки минимума 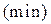 называются точками экстремума функции
называются точками экстремума функции  , а соответствующие значения функции – экстремальными значениями.
, а соответствующие значения функции – экстремальными значениями.
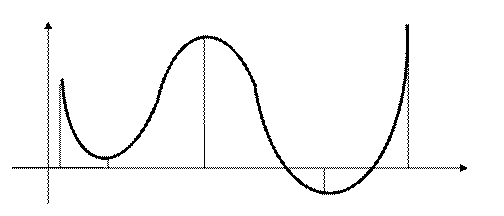 Замечание 2. Не следует, вообще говоря, считать, что максимум и минимум функции являются соответственно её наибольшим и наимень-шим значениями.
Замечание 2. Не следует, вообще говоря, считать, что максимум и минимум функции являются соответственно её наибольшим и наимень-шим значениями.
y
0 а х 1 х 2 х 3 b x
Здесь х 1, х 3 - точки минимума, х 2 - точка максимума функции  , а
, а

Из теоремы Ролля следует необходимое условие существования экстремума функции:
Если функция  дифференцируемая и имеет экстремум в точке х 0, то в этой точке
дифференцируемая и имеет экстремум в точке х 0, то в этой точке 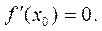
Как обстоит дело в точках, где производная не существует? Например, очевидно, что функция  имеет минимум при
имеет минимум при 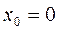 , где она не дифференцируемая.
, где она не дифференцируемая.
Таким образом, окончательно можем сформулировать
Необходимое условие экстремума. Если непрерывная функция  имеет в точке х 0 экстремум, то в этой точке
имеет в точке х 0 экстремум, то в этой точке 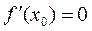 либо не существует.
либо не существует.
Определение 3. Точки, в которых 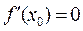 называются стационар-ными. Стационарные точки и точки, в которых производная не сущест-вует, называются критическими.
называются стационар-ными. Стационарные точки и точки, в которых производная не сущест-вует, называются критическими.
Замечание 3. Очевидно, что не всякая критическая точка является точкой экстремума. Например, 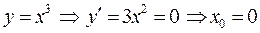 - критическая точка, которая не является точкой экстремума (см. график функции
- критическая точка, которая не является точкой экстремума (см. график функции 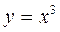 ).
).
Как выделить из критических точек точки экстремума? Для этого существуют достаточные условия экстремума.
6.3. Достаточные условия экстремума
Так как точка максимума разделяет интервалы возрастания и убывания, а точка минимума - убывания и возрастания, то получаем
Первое достаточное условие экстремума. Если при переходе через критическую точку слева направо производная меняет знак с плюса на минус, то это точка 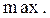 Если – с минуса на плюс, то это точка
Если – с минуса на плюс, то это точка 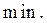
Второе достаточное условие экстремума. Пусть точка х 0 является стационарной точкой функции  , которая имеет непрерывную произ-водную второго порядка в окрестности этой точки. Тогда, если
, которая имеет непрерывную произ-водную второго порядка в окрестности этой точки. Тогда, если 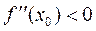 , то точка х 0 – точка
, то точка х 0 – точка  если
если 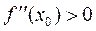 , то -
, то - 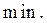
Действительно, запишем для функции  формулу Тейлора при
формулу Тейлора при  в окрестности точки х 0:
в окрестности точки х 0:
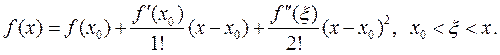
Так как точка х 0 является стационарной точкой функции  , то
, то 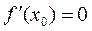 и из формулы Тейлора следует
и из формулы Тейлора следует

Отсюда в силу непрерывности 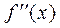 имеем:
имеем:
1. Если 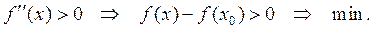
2. Если 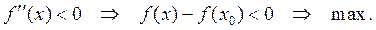
Пример 2. Исследовать на экстремум функцию  .
.
Найдём производную данной функции
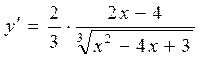 ,
,
из которой определим критические точки: 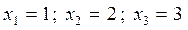 .
.
Построим таблицу
| х | 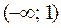
| 
| 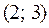
| 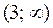
| |||
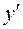
| - | 
| + | - | 
| + | |
| у | 
| 
| 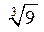
| 
| 
| ||
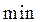
| 
| 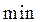
|
Итак, функция  имеет экстремум (максимум), равный
имеет экстремум (максимум), равный 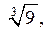 в точке
в точке 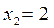 и два экстремума (минимума), равных 0, в точках
и два экстремума (минимума), равных 0, в точках  Или сокращенно:
Или сокращенно: 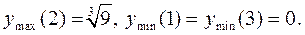
6.4. Наибольшее и наименьшее значения функции на отрезке
Пусть задана непрерывная на 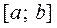 функция
функция  . Она достигает своих наибольшего и наименьшего значений либо во внутренних крити-ческих точках либо на концах отрезка
. Она достигает своих наибольшего и наименьшего значений либо во внутренних крити-ческих точках либо на концах отрезка 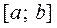 . Отсюда следует
. Отсюда следует
Правило. Для того, чтобы найти наибольшее (наименьшее) значение  на
на 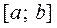 необходимо:
необходимо:
1. Найти критические точки, принадлежащие данному отрезку 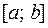 ;
;
2. Вычислить значения функции  в критических точках и на концах отрезка
в критических точках и на концах отрезка 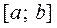 ;
;
3. Выбрать из полученных значений наибольшее и наименьшее.
Пример 3. Найти наибольшее и наименьшее значения функции
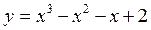 на отрезке
на отрезке  .
.
Находим критические точки
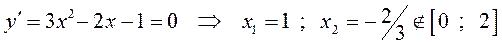 .
.
Вычисляем значения функции в критической точке х = 1 и на кон-цах рассматриваемого отрезка  :
:
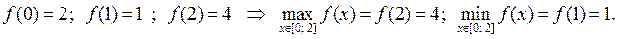
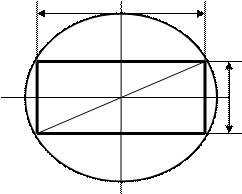 Пример 4.* Из круглого бревна, диаметр которого равен d, требуется вырезать балку прямоугольного поперечного сечения. Каковы должны быть ширина и высота этого сечения, чтобы балка оказывала наибольшее сопротивление на изгиб, если сопротивление на изгиб вычисляется по формуле
Пример 4.* Из круглого бревна, диаметр которого равен d, требуется вырезать балку прямоугольного поперечного сечения. Каковы должны быть ширина и высота этого сечения, чтобы балка оказывала наибольшее сопротивление на изгиб, если сопротивление на изгиб вычисляется по формуле 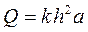 , где k - упругая постоянная, a - ширина, h - высота сечения балки. а
, где k - упругая постоянная, a - ширина, h - высота сечения балки. а
Обозначим  .
.
Тогда 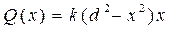 и
и
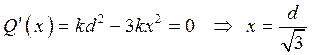 h
h
Покажем, что это точка максимума,
воспользовавшись вторым достаточным
условием экстремума
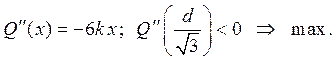
Лекция № 22.
6.5. Выпуклость, вогнутость, точки перегиба
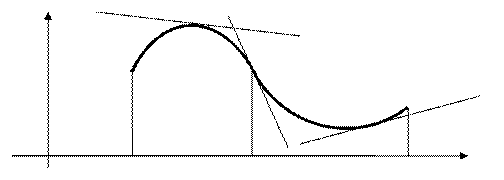
Определение 1. Линия  называется выпуклой (вогнутой) на
называется выпуклой (вогнутой) на  , если все точки линии, кроме точки касания, лежат ниже (выше) любой её касательной на этом интервале. Точка, отделяющая выпуклую часть графика от вогнутой, называется точкой перегиба.
, если все точки линии, кроме точки касания, лежат ниже (выше) любой её касательной на этом интервале. Точка, отделяющая выпуклую часть графика от вогнутой, называется точкой перегиба.
y
О а х 0 b x
Здесь на интервале 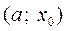 функция
функция  выпукла, на интервале
выпукла, на интервале 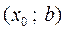 функция
функция  вогнута, х 0 - точка перегиба.
вогнута, х 0 - точка перегиба.
Для определения интервалов выпуклости (вогнутости) используется условие их существования.
Теорема 1. Если для 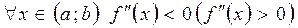 , то на этом интервале линия выпукла (вогнута).
, то на этом интервале линия выпукла (вогнута).
Пусть 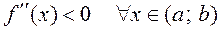 . Уравнение касательной, проведённой в точке
. Уравнение касательной, проведённой в точке 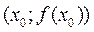 , имеет вид
, имеет вид 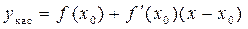 , а уравнение линии
, а уравнение линии 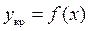 . Рассмотрим разность
. Рассмотрим разность
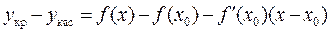 . (1)
. (1)
К первым двум членам правой части выражения (1) применим теорему Лагранжа и рассмотрим случай 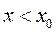
 .
.
Ещё раз воспользуемся теоремой Лагранжа
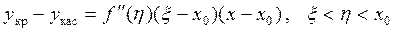 .
.
В этом случае 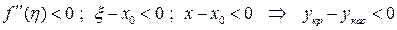 , а это означает, что на интервале
, а это означает, что на интервале 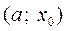 линия
линия  выпукла.
выпукла.
Аналогично теорема доказывается и для случая 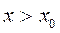 .
.
Точно также можно доказать условие вогнутости.
Из определения точки перегиба следует:
Необходимое условие точки перегиба. Если х 0 - точка перегиба функ-ции  , то в этой точке
, то в этой точке 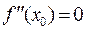 либо не существует.
либо не существует.
С учетом теоремы об условиях выпуклости (вогнутости) получаем
Достаточное условие точки перегиба. Если 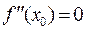 или не существует и при переходе через эту точку
или не существует и при переходе через эту точку 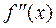 меняет знак, то точка х 0 является точкой перегиба.
меняет знак, то точка х 0 является точкой перегиба.
Пример 1. Найти интервалы выпуклости, вогнутости, точки перегиба функции 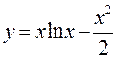 .
.
Вычислим производные: 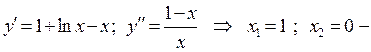 не принадлежит области определения функции. Построим таблицу
не принадлежит области определения функции. Построим таблицу
| х | 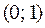
| 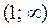
| |
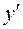
| + | - | |
| у | 
| перегиб | 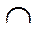
|
Здесь на интервале 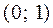 функция
функция  вогнута, на интервале
вогнута, на интервале 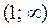 функция
функция  выпукла, х 0 = 1 - точка перегиба.
выпукла, х 0 = 1 - точка перегиба.
6.6. Асимптоты линий
Определение 2. Прямая называется асимптотой линии 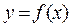 , если расстояние от текущей точки М линии до этой прямой при
, если расстояние от текущей точки М линии до этой прямой при 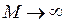 стремится к нулю.
стремится к нулю.
Из определения асимптоты следует:
1. Прямая 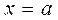 является вертикальной асимптотой, если хотя бы один из односторонних пределов
является вертикальной асимптотой, если хотя бы один из односторонних пределов  равен
равен 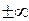 .
.
2. Если для линии 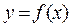 прямая
прямая  - наклонная асимптота, то
- наклонная асимптота, то 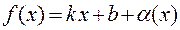 , где
, где  .
.

у
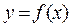
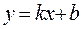
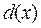
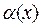
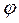
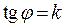 х
х
Из рисунка 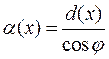 , т.е. расстояние
, т.е. расстояние 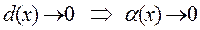 .
.
Для нахождения асимптот линий применяется
Теорема 2. Если для линии 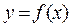 прямая
прямая  является асимп-тотой при
является асимп-тотой при 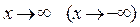 , то
, то 
 . Верно и обратное.
. Верно и обратное.
Пусть  является асимптотой для
является асимптотой для 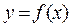 . Это означает, что
. Это означает, что 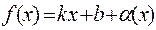 и тогда
и тогда 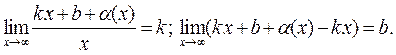
Обратно. По теореме о пределе функции имеем равенство
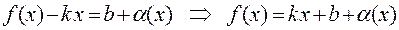 ,
,
т.е. прямая 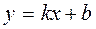 является асимптотой линии
является асимптотой линии 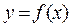 .
.
Пример 2. Найти асимптоты линии 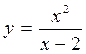 .
.
Имеется вертикальная асимптота 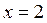 , так как
, так как 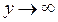 при
при 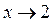 .
.
Определим наклонную асимптоту: угловой коэффициент  свободный член
свободный член 
Замечание. Иногда значения пределов могут быть различными при  и
и 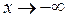 . В этом случае говорят об односторонних асимптотах.
. В этом случае говорят об односторонних асимптотах.
Например, для линии 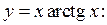
 , а
, а  . А коэффициент b находим с помощью правила Лопиталя
. А коэффициент b находим с помощью правила Лопиталя
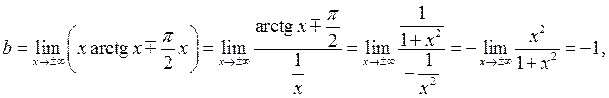
т.е. линия имеет правостороннюю  и левостороннюю
и левостороннюю 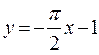
асимптоты.
6.7. Общий план исследования функций и построение графиков
Для исследования и построения графиков функций удобно придер-живаться следующей последовательности действий:
1. Найти область определения функции.
2. Выяснить чётность, нечётность или функция общего вида.
3. Определить точки пересечения графика функции с осями координат.
4. Найти точки разрыва функции и выяснить их характер.
5. Определить интервалы возрастания, убывания, точки экстремума.
6. Найти интервалы выпуклости, вогнутости, точки перегиба.
7. Найти асимптоты.
8. По полученным результатам построить график функции.
Пример 3. Построить график функции  , где
, где 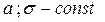 .
.
1.  2. Функция общего вида.
2. Функция общего вида.
3. 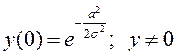 . 4. Точек разрыва нет, функция непрерывна.
. 4. Точек разрыва нет, функция непрерывна.
5. Находим производную 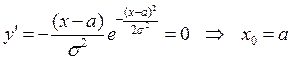 - крити-ческая точка на экстремум. Построим таблицу
- крити-ческая точка на экстремум. Построим таблицу
<
Date: 2015-09-02; view: 534; Нарушение авторских прав