
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ЗАДАНИЕ N 42 сообщить об ошибке Тема: Дифференциальное исчисление ФНП
|
|
Начало формы




Конец формы
Частная производная 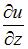 функции
функции 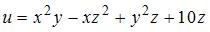 имеет вид …
имеет вид …

| 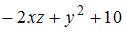
|
Решение:
При вычислении частной производной 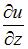 по переменной
по переменной 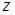 , переменные
, переменные 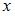 и
и 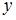 рассматриваем как постоянные величины. Тогда
рассматриваем как постоянные величины. Тогда
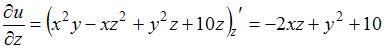 .
.
 ЗАДАНИЕ N 43 сообщить об ошибке
ЗАДАНИЕ N 43 сообщить об ошибке
Тема: Непрерывность функции, точки разрыва
Начало формы




Конец формы
Точка разрыва функции 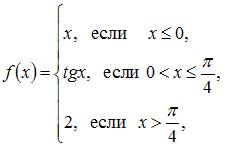 равна …
равна …

| 
|
 ЗАДАНИЕ N 44 сообщить об ошибке
ЗАДАНИЕ N 44 сообщить об ошибке
Тема: Приложения определенного интеграла
Начало формы




Конец формы
Объем тела, полученного вращением вокруг оси 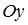 криволинейной трапеции, ограниченной параболой
криволинейной трапеции, ограниченной параболой 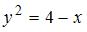 и осью
и осью 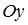 , равен …
, равен …

| 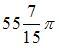
|
Решение:
Вычислим точки пересечения параболы 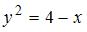 с осью
с осью 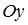 , решив уравнение
, решив уравнение 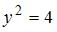 . Получим точки
. Получим точки  и
и 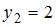 .
.
Тогда объем тела, полученного вращением соответствующей криволинейной трапеции вокруг оси 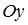 , вычисляется как:
, вычисляется как:
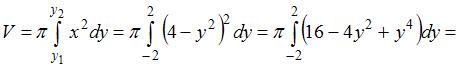
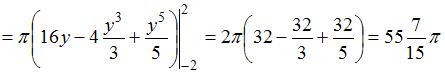 .
.
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Приложения определенного интеграла
Начало формы




Конец формы
Площадь фигуры, изображенной на рисунке
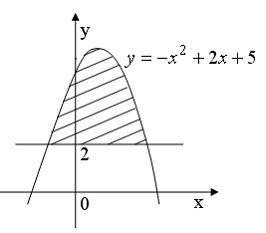
равна …

| 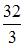
|
Решение:
Площадь данной фигуры можно вычислить по формуле 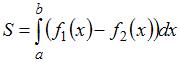 , где
, где 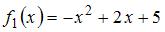 ,
, 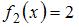 ,
, 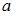 – «левая»,
– «левая», 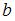 – «правая» точки пересечения параболы
– «правая» точки пересечения параболы 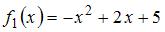 и прямой
и прямой 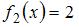 . Определим значения
. Определим значения 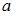 и
и 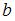 , решив уравнение
, решив уравнение 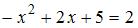 . Получаем
. Получаем 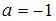 ,
, 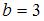 . Тогда
. Тогда
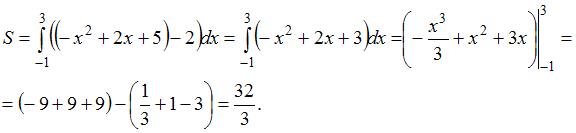
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Непрерывность функции, точки разрыва
Начало формы




Конец формы
Функция 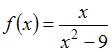 непрерывна на отрезке …
непрерывна на отрезке …

| 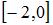
|
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Основные методы интегрирования
Начало формы




Конец формы
Множество первообразных функции 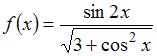 имеет вид …
имеет вид …

| 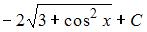
|
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Начало формы




Конец формы
Частная производная 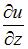 функции
функции 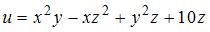 имеет вид …
имеет вид …

| 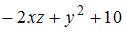
|
 ЗАДАНИЕ N 26 сообщить об ошибке
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Начало формы




Конец формы
Частная производная второго порядка 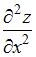 функции
функции 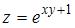 имеет вид …
имеет вид …

| 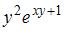
|
Решение:
При вычислении частной производной функции 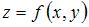 по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
 и
и
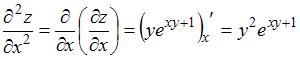 .
.
 ЗАДАНИЕ N 27 сообщить об ошибке
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Непрерывность функции, точки разрыва
Начало формы




Конец формы
Точка 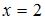 является точкой разрыва функции …
является точкой разрыва функции …

| 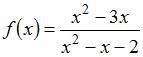
|
Решение:
Точку 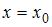 называют точкой разрыва функции
называют точкой разрыва функции 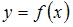 , если она не является непрерывной в этой точке. В частности, точками разрыва данных функций являются точки, в которых знаменатель равен нулю, то есть
, если она не является непрерывной в этой точке. В частности, точками разрыва данных функций являются точки, в которых знаменатель равен нулю, то есть  , или:
, или:
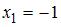
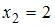 .
.
Точка 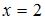 :
:
не является точкой разрыва функции 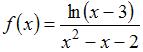 , так как область определения функции
, так как область определения функции 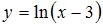 имеет вид
имеет вид 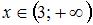 , и
, и 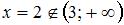 ;
;
не является точкой разрыва функции 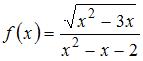 , так как область определения функции
, так как область определения функции 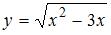 имеет вид
имеет вид 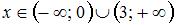 , и
, и 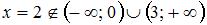 ;
;
не является точкой разрыва функции 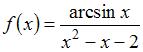 , так как область определения функции
, так как область определения функции 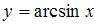 имеет вид
имеет вид 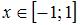 , и
, и 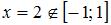 .
.
Таким образом, точка 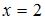 является точкой разрыва функции
является точкой разрыва функции 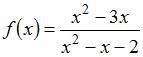 .
.
 ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Основные методы интегрирования
Начало формы




Конец формы
Множество первообразных функции 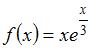 имеет вид …
имеет вид …

| 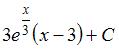
|
 ЗАДАНИЕ N 29 сообщить об ошибке
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Приложения определенного интеграла
Начало формы




Конец формы
Площадь фигуры, ограниченной параболой  и осью
и осью  , равна …
, равна …

|
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Непрерывность функции, точки разрыва
Начало формы




Конец формы
Количество точек разрыва функции 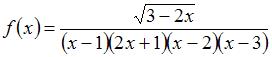 равно …
равно …

|
Решение:
Точку 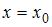 называют точкой разрыва функции
называют точкой разрыва функции  , если она не является непрерывной в этой точке. В частности, точками разрыва данной функции могут являться точки, в которых знаменатель равен нулю, то есть
, если она не является непрерывной в этой точке. В частности, точками разрыва данной функции могут являться точки, в которых знаменатель равен нулю, то есть 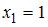 ,
, 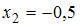 ,
, 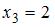 ,
,  . Однако область определения функции
. Однако область определения функции 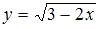 определяется как
определяется как 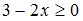 , то есть имеет вид
, то есть имеет вид 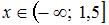 . Тогда
. Тогда 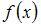 имеет две точки разрыва:
имеет две точки разрыва: 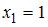 ,
, 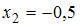 , удовлетворяющие условию
, удовлетворяющие условию 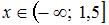 .
.
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Приложения определенного интеграла
Начало формы




Конец формы
Площадь фигуры, изображенной на рисунке
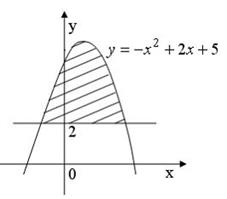
равна …

| 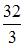
|
Решение:
Площадь данной фигуры можно вычислить по формуле 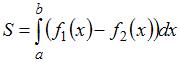 , где
, где 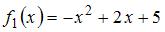 ,
, 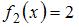 ,
, 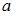 – «левая»,
– «левая», 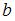 – «правая» точки пересечения параболы
– «правая» точки пересечения параболы 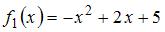 и прямой
и прямой 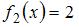 . Определим значения
. Определим значения 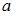 и
и 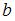 , решив уравнение
, решив уравнение 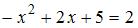 . Получаем
. Получаем 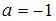 ,
, 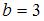 . Тогда
. Тогда
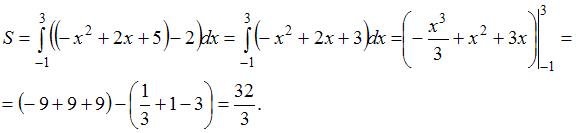
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Начало формы




Конец формы
Частная производная 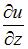 функции
функции 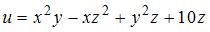 имеет вид …
имеет вид …

| 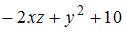
|
Решение:
При вычислении частной производной 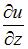 по переменной
по переменной 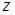 , переменные
, переменные 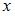 и
и 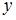 рассматриваем как постоянные величины. Тогда
рассматриваем как постоянные величины. Тогда
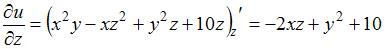 .
.
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Основные методы интегрирования
Начало формы




Конец формы
Множество первообразных функции 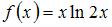 имеет вид …
имеет вид …

| 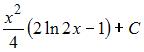
|
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции методом интегрирования по частям по формуле 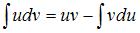 . Тогда
. Тогда
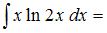
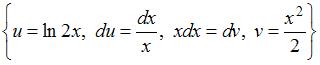
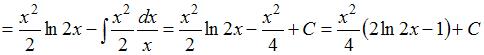 .
.
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Приложения определенного интеграла
Начало формы




Конец формы
Площадь фигуры, изображенной на рисунке

равна …

| 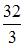
|
Решение:
Площадь данной фигуры можно вычислить по формуле 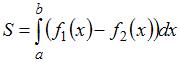 , где
, где 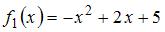 ,
, 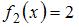 ,
, 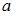 – «левая»,
– «левая», 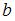 – «правая» точки пересечения параболы
– «правая» точки пересечения параболы 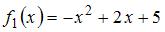 и прямой
и прямой 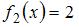 . Определим значения
. Определим значения 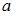 и
и 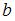 , решив уравнение
, решив уравнение 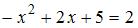 . Получаем
. Получаем 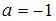 ,
, 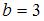 . Тогда
. Тогда
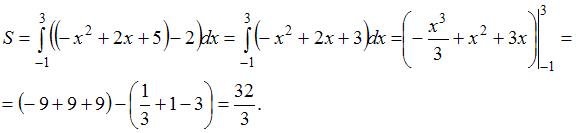
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Начало формы




Конец формы
Смешанная частная производная второго порядка 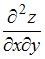 функции
функции 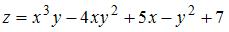 имеет вид …
имеет вид …

| 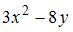
|
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Основные методы интегрирования
Начало формы




Конец формы
Множество первообразных функции 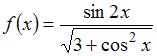 имеет вид …
имеет вид …

| 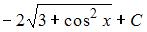
|
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Непрерывность функции, точки разрыва
Начало формы




Конец формы
Для функции 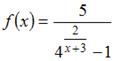 точка
точка 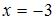 является точкой …
является точкой …

| разрыва первого рода |
Решение:
Вычислим односторонние пределы функции 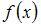 в точке
в точке 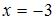 :
:
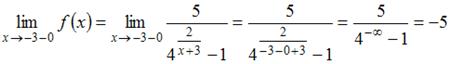 ;
;
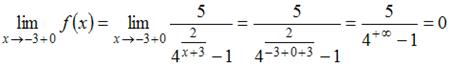 .
.
Так как односторонние пределы функции 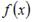 в точке
в точке  существуют, конечны, но не равны между собой, то точка
существуют, конечны, но не равны между собой, то точка 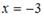 является точкой разрыва первого рода.
является точкой разрыва первого рода.
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Непрерывность функции, точки разрыва
Начало формы




Конец формы
Точка 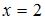 является точкой разрыва функции …
является точкой разрыва функции …

| 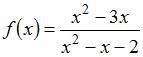
|
Решение:
Точку 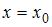 называют точкой разрыва функции
называют точкой разрыва функции 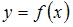 , если она не является непрерывной в этой точке. В частности, точками разрыва данных функций являются точки, в которых знаменатель равен нулю, то есть
, если она не является непрерывной в этой точке. В частности, точками разрыва данных функций являются точки, в которых знаменатель равен нулю, то есть  , или:
, или:
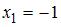
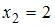 .
.
Точка 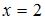 :
:
не является точкой разрыва функции 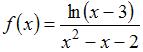 , так как область определения функции
, так как область определения функции 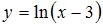 имеет вид
имеет вид 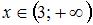 , и
, и 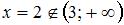 ;
;
не является точкой разрыва функции 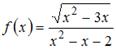 , так как область определения функции
, так как область определения функции 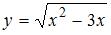 имеет вид
имеет вид 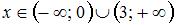 , и
, и 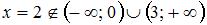 ;
;
не является точкой разрыва функции  , так как область определения функции
, так как область определения функции 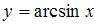 имеет вид
имеет вид 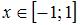 , и
, и 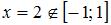 .
.
Таким образом, точка 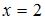 является точкой разрыва функции
является точкой разрыва функции 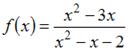 .
.
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Начало формы




Конец формы
Частная производная 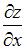 функции
функции  имеет вид …
имеет вид …

| 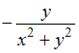
|
Решение:
При вычислении частной производной 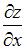 по переменной
по переменной 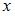 , переменную
, переменную 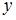 рассматриваем как постоянную величину. Тогда
рассматриваем как постоянную величину. Тогда
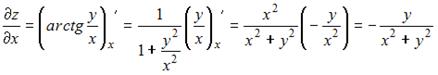 .
.
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Приложения определенного интеграла
Начало формы




Конец формы
Площадь фигуры, изображенной на рисунке
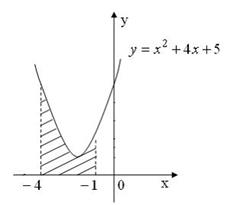
равна …

|
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Основные методы интегрирования
Начало формы




Конец формы
Множество первообразных функции 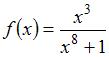 имеет вид …
имеет вид …

| 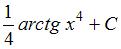
|
 ЗАДАНИЕ N 33 сообщить об ошибке
ЗАДАНИЕ N 33 сообщить об ошибке
Тема: Приложения определенного интеграла
Начало формы




Конец формы
Площадь фигуры, изображенной на рисунке
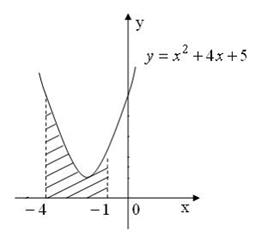
равна …

|
Решение:
Площадь данной фигуры можно вычислить по формуле 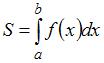 , где
, где 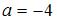 ,
, 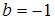 , а
, а 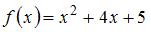 . Тогда
. Тогда
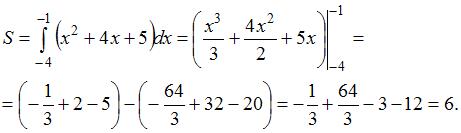
 ЗАДАНИЕ N 34 сообщить об ошибке
ЗАДАНИЕ N 34 сообщить об ошибке
Тема: Непрерывность функции, точки разрыва
Начало формы




Конец формы
Для функции 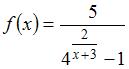 точка
точка 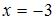 является точкой …
является точкой …

| разрыва первого рода |
Решение:
Вычислим односторонние пределы функции 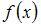 в точке
в точке 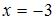 :
:
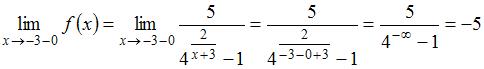 ;
;
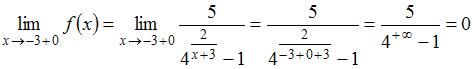 .
.
Так как односторонние пределы функции 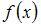 в точке
в точке 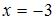 существуют, конечны, но не равны между собой, то точка
существуют, конечны, но не равны между собой, то точка 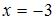 является точкой разрыва первого рода.
является точкой разрыва первого рода.
 ЗАДАНИЕ N 35 сообщить об ошибке
ЗАДАНИЕ N 35 сообщить об ошибке
Тема: Основные методы интегрирования
Начало формы




Конец формы
Множество первообразных функции 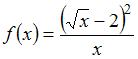 имеет вид …
имеет вид …

| 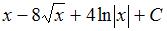
|
 ЗАДАНИЕ N 36 сообщить об ошибке
ЗАДАНИЕ N 36 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Начало формы




Конец формы
Частная производная 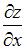 функции
функции  имеет вид …
имеет вид …

| 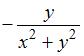
|
Решение:
При вычислении частной производной 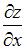 по переменной
по переменной 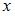 , переменную
, переменную 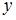 рассматриваем как постоянную величину. Тогда
рассматриваем как постоянную величину. Тогда
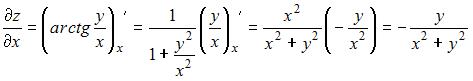 .
.
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Непрерывность функции, точки разрыва
Начало формы




Конец формы
Точка разрыва функции 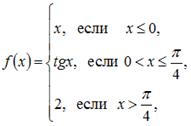 равна …
равна …

| 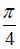
|
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Начало формы




Конец формы
Частная производная 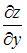 функции
функции 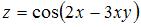 имеет вид …
имеет вид …

| 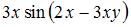
|
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Основные методы интегрирования
Начало формы




Конец формы
Множество первообразных функции  имеет вид …
имеет вид …

| 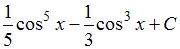
|
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда
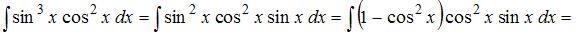
Произведем замену 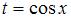 ,
, 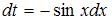 ,
, 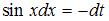 :
:
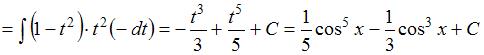 .
.
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Приложения определенного интеграла
Начало формы




Конец формы
Площадь фигуры, изображенной на рисунке
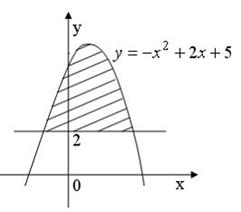
равна …

| 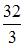
|
Решение:
Площадь данной фигуры можно вычислить по формуле 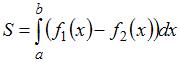 , где
, где 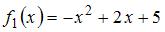 ,
, 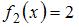 ,
, 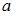 – «левая»,
– «левая», 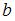 – «правая» точки пересечения параболы
– «правая» точки пересечения параболы 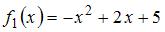 и прямой
и прямой 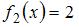 . Определим значения
. Определим значения 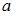 и
и 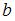 , решив уравнение
, решив уравнение 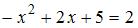 . Получаем
. Получаем 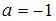 ,
, 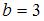 . Тогда
. Тогда
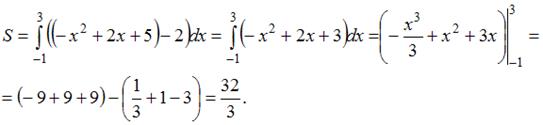
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Начало формы




Конец формы
Полный дифференциал функции 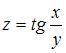 имеет вид …
имеет вид …

| 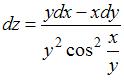
|
Решение:
Полный дифференциал функции нескольких переменных равен сумме произведений частных производных этой функции на дифференциалы соответствующих независимых переменных, то есть
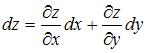 .
.
Тогда
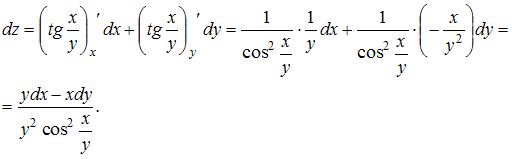
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Основные методы интегрирования
Начало формы




Конец формы
Множество первообразных функции 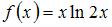 имеет вид …
имеет вид …

| 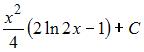
|
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции методом интегрирования по частям по формуле 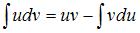 . Тогда
. Тогда
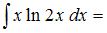
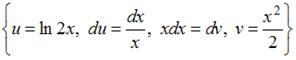
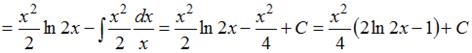 .
.
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Непрерывность функции, точки разрыва
Начало формы




Конец формы
Количество точек разрыва функции 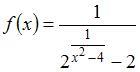 равно …
равно …

|
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Приложения определенного интеграла
Начало формы




Конец формы
Площадь фигуры, изображенной на рисунке

равна …

| 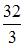
|
Решение:
Площадь данной фигуры можно вычислить по формуле 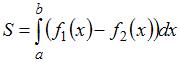 , где
, где 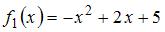 ,
, 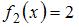 ,
, 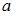 – «левая»,
– «левая», 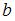 – «правая» точки пересечения параболы
– «правая» точки пересечения параболы 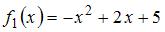 и прямой
и прямой 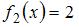 . Определим значения
. Определим значения 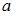 и
и 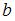 , решив уравнение
, решив уравнение 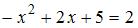 . Получаем
. Получаем 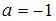 ,
, 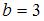 . Тогда
. Тогда
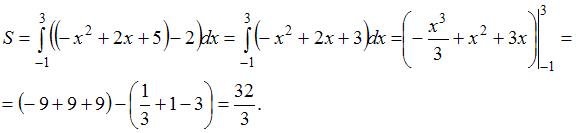
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Непрерывность функции, точки разрыва
Начало формы




Конец формы
Количество точек разрыва функции 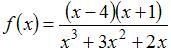 равно …
равно …

|
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Приложения определенного интеграла
Начало формы




Конец формы
Площадь фигуры, изображенной на рисунке
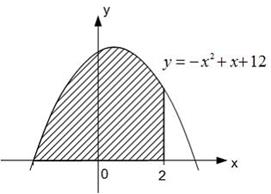
равна …

| 
|
Решение:
Площадь данной фигуры можно вычислить по формуле 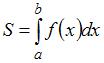 , где
, где 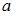 – «левая» точка пересечения параболы и оси
– «левая» точка пересечения параболы и оси 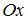 ,
,  , а
, а 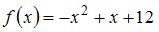 . Определим точки пересечения параболы и оси
. Определим точки пересечения параболы и оси 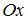 , решив уравнение
, решив уравнение 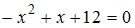 . Получаем:
. Получаем: 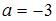 . Тогда
. Тогда
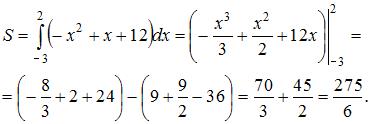
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Основные методы интегрирования
Начало формы




Конец формы
Множество первообразных функции 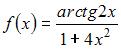 имеет вид …
имеет вид …

| 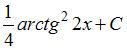
|
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда
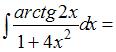
Произведем замену 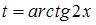 ,
, 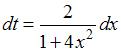 ,
, 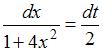 :
:
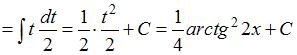 .
.
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Начало формы




Конец формы
Частная производная второго порядка 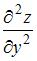 функции
функции 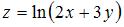 имеет вид …
имеет вид …

| 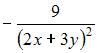
|
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Начало формы




Конец формы
Смешанная частная производная второго порядка 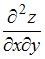 функции
функции 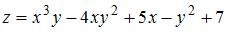 имеет вид …
имеет вид …

| 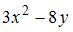
|
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Непрерывность функции, точки разрыва
Начало формы




Конец формы
Точка 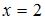 является точкой разрыва функции …
является точкой разрыва функции …

| 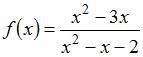
|
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Основные методы интегрирования
Начало формы




Конец формы
Множество первообразных функции 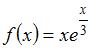 имеет вид …
имеет вид …

| 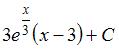
|
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Приложения определенного интеграла
Начало формы




Конец формы
Объем тела, полученного вращением вокруг оси 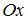 криволинейной трапеции, ограниченной параболой
криволинейной трапеции, ограниченной параболой 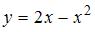 и осью
и осью 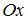 , равен …
, равен …

| 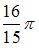
|
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Начало формы




Конец формы
Частная производная второго порядка 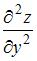 функции
функции 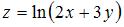 имеет вид …
имеет вид …

| 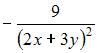
|
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Приложения определенного интеграла
Начало формы




Конец формы
Объем тела, полученного вращением
Date: 2015-09-02; view: 525; Нарушение авторских прав