
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Правило Лопиталя
|
|
При раскрытии неопределенностей 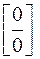 ,
, 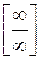 кроме классических методов вычисления пределов, во многих случаях можно пользоваться правилом Лопиталя:
кроме классических методов вычисления пределов, во многих случаях можно пользоваться правилом Лопиталя:
Eсли 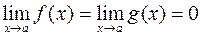 или
или  и существует предел отношения их производных
и существует предел отношения их производных 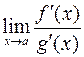 , то
, то  .
.
Это правило справедливо и в случае 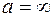 .
.
Пример1. Применяя правило Лопиталя, найти пределы:
а)  ; б)
; б) 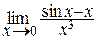 ; в)
; в) 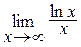 .
.
Решение. Убедившись, что имеет место случай 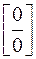 или
или 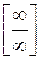 , применяем правило Лопиталя.
, применяем правило Лопиталя.
а) 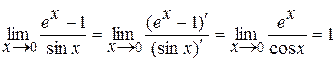 ,
,
б) 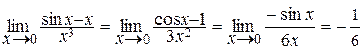 .
.
Здесь мы дважды применили правило Лопиталя и воспользовались первым замечательным пределом.
в)  .
.
При раскрытии неопределенностей 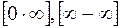 для применения правила Лопиталя, данное выражение, путем алгебраических преобразований, надо преобразовать к неопределенностям
для применения правила Лопиталя, данное выражение, путем алгебраических преобразований, надо преобразовать к неопределенностям 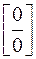 или
или 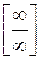 .
.
Пример 2. Найти пределы:
а)  ; б)
; б) 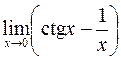 .
.
Решение: а) Имеем неопределенность 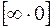 . Приведем эту неопределенность к неопределенности
. Приведем эту неопределенность к неопределенности 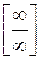 , а затем применим правило Лопиталя:
, а затем применим правило Лопиталя:
 .
.
При раскрытии неопределенностей 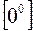 ,
, 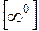 ,
, 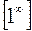 рекомендуется найти предварительно предел логарифма искомой функции.
рекомендуется найти предварительно предел логарифма искомой функции.
Пример 3.Вычислить 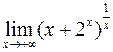 .
.
Решение. Имеем неопределенность 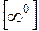 . Введем обозначение
. Введем обозначение
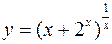 , тогда
, тогда  .
. 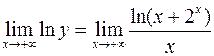 .
.
Получили неопределенность 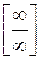 , применяем правило Лопиталя:
, применяем правило Лопиталя:
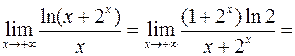
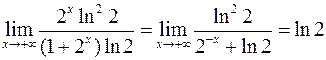 . Так как
. Так как  . Следовательно
. Следовательно 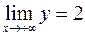 .
.
Варианты заданий РГР
Задача1. Найти производные функций:
1. а) 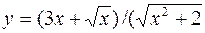 б)
б) 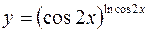
в) 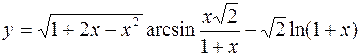 .
.
2. а) 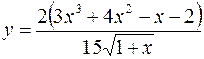 б)
б) 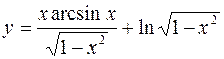
в) 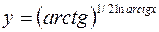 .
.
3. а) 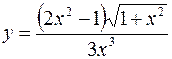 б)
б) 
в) 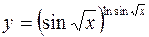 .
.
4. а) 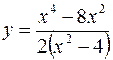 б)
б) 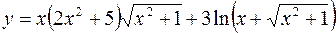
в) 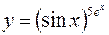 .
.
5. а) 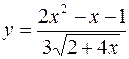 б)
б) 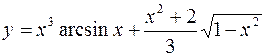
в) 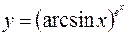 .
.
6. а)  б)
б) 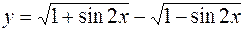
в) 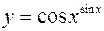 .
.
7. а) 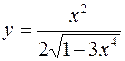 б)
б) 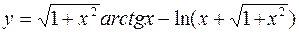
в) 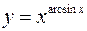 .
.
8. а) 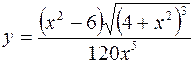 б)
б) 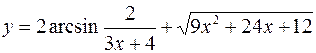
в) 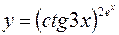 .
.
9. а) 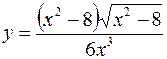 б)
б) 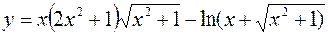
в) 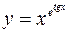 .
.
10. а)  б)
б) 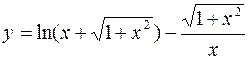
в)  .
.
11. а) 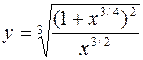 б)
б) 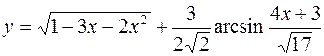
в)  .
.
12. а) 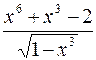 б)
б) 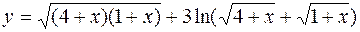
в) 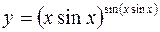 .
.
13. а)  б)
б) 
в) 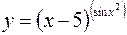 .
.
14. а) 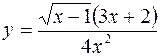 б)
б) 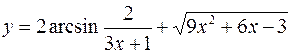
в) 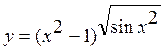 .
.
15.а) 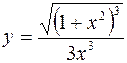 б)
б) 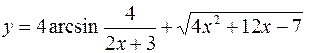
в) 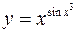 .
.
16. а) 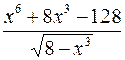 б)
б) 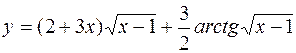
в) 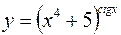 .
.
17. а)  б)
б) 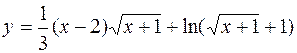
в) 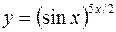 .
.
18. а) 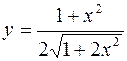 б)
б) 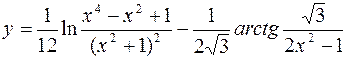
в) 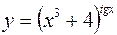 .
.
19. а) 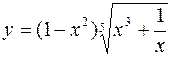 б)
б) 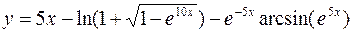
в)  .
.
20. а)  б)
б) 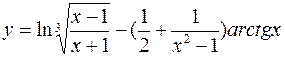
в) 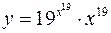 .
.
21. а) 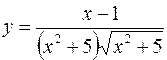 б)
б) 
в) 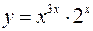 .
.
22. а) 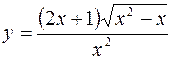 б)
б) 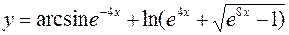
в)  .
.
23. а) 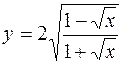 б)
б) 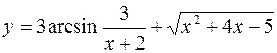
в)  .
.
24. а)  б)
б) 
в) 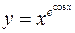 .
.
25. а) 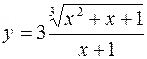 б)
б) 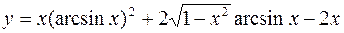
в) 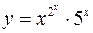 .
.
26  б)
б) 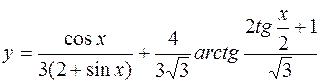
в) 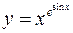 .
.
27. а) 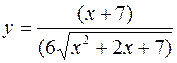
б) 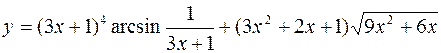
в) 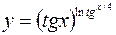 .
.
28. а) 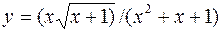 б)
б) 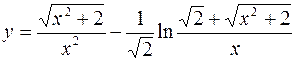
в) 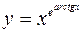 .
.
29. а) 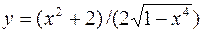 б)
б) 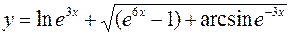
в) 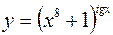 .
.
30. а) 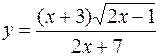 б)
б) 
в) 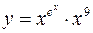 .
.
Задача 2. Составить уравнение касательной к кривой, заданной параметрически, в точке, соответствующей значению параметра 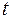 .
.
1. 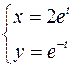 ,
, 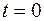 .
.
2. 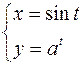 ,
, 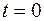 .
.
3. 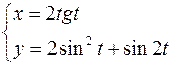 ,
, 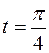 .
.
4. 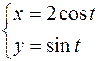 ,
, 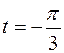 .
.
5. 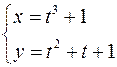 ,
, 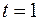 .
.
6. 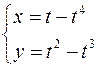 ,
, 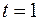 .
.
7. 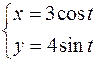 ,
, 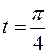 .
.
8.  ,
, 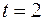 .
.
9.  ,
, 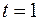 .
.
10. 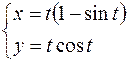 ,
, 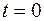 .
.
11. 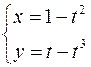 ,
, 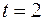 .
.
12. 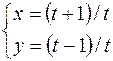 ,
, 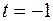 .
.
13. 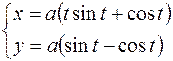 ,
, 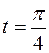 .
.
14. 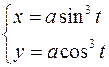 ,
, 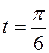 .
.
15. 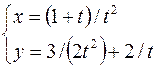 ,
, 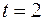 .
.
16.  ,
, 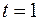 .
.
17. 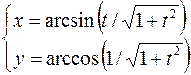 ,
, 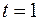 .
.
18. 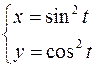 ,
, 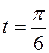 .
.
19.  ,
, 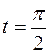 .
.
20. 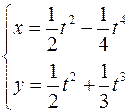 ,
, 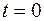 .
.
21. 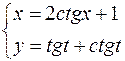 ,
, 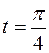 .
.
22. 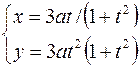 ,
, 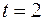 .
.
23. 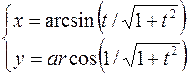 ,
, 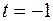 .
.
24. 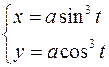 ,
,  .
.
25. 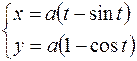 ,
,  .
.
26. 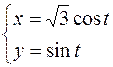 ,
,  .
.
27.  ,
, 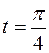 .
.
28.  ,
, 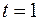 .
.
29.  ,
, 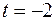 .
.
30. 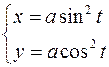 ,
, 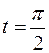 .
.
Задача 3. Найти значение 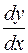 в точке М (x0, y 0) для функций, заданных неявно.
в точке М (x0, y 0) для функций, заданных неявно.
1. x 3 – 2 x 2 y 2 + 5 x + y – 5 = 0, M (1; 1).
2. x 2 + 2 xy 2 + 3 y 4 – 6 = 0, M (1; –1).
3. x 4 – 6 x 2 y 2 + 9 y 2 – 5 x 2 + 15 y 2 + 4 = 0, M (2; 1).
4. x 3 + y 3 – 3 xy + 1 = 0, M (–2;1).
5. 5 x 2 + 3 xy – 2 y 2 + 2 = 0, M (0; 1).
6. x 2 + y 2 – 4 x – 10 y + 19 = 0, M (3; 2).
7. x 3 + x 2 y + y 2 – 13 = 0, M (1; 3).
8. x 3 – 2 x 2 + y 2 = 0, M (1; 1).
9. x 2 + 5 xy + y 2 – 2 x + y – 6 = 0, M (1; 1).
10. x 5 + y 5 – 2 xy = 0, M (1; 1).
11. x 2 + xy + y 2 = 7, M (–1; –2).
12. 2 x 3 – xy + y – 2 = 0, M (1; 5).
13. 3 x 2 – xy + y – 3 = 0, M (1; –2).
14. x 2 + 2 y 2 + 6 x – 4 y – 13 = 0, M (1; –1).
15. 3 x 2 – 5 y2 – 6 x – 20 y + 25 = 0, M (2; 1).
16. 4 x 2 + y 2 + 8 x – 4 y + 3 = 0, M (0; 1).
17. 2 x 2 – 9 y 2 + 4 x + 18 y + 11 = 0, M (2; –1).
18. x 3 – xy + y + 7 = 0, M (–1; –3).
19. x 4 – y 2 – y – 1 = 0, M (1; 0).
20. x 3 + 2 xy 2 + y + 11 = 0, M (–1; –2).
21. x 3 + 5 xy + y 3 – 7 = 0, M (1; 1).
22. 3 x 2 – xy + y 3 – x = 0, M (0; 2).
23. x 6 + y 6 – 2 xy = 0, M (1; 1).
24. x 2 + x 2 y – y 2 – y = 0, M (1; 1).
25. 7 x 2 + xy – y 3 + 3 = 0, M (1; –2).
26. x 2 y 2 + xy + x 2 – 7 = 0, M (1; 2).
27. 2 x 5 + y 5 – 2 xy + 26 = 0, M (1; –2).
28. 3 x 2 – xy + y 2 + x – 34 = 0, M (–2; 4).
29. x 2 – x 2 y + y 2 = 13, M (–1; –3).
30. x 2 y 2 – 4 y 3 – x = 4, M (0; –1).
Задача 4. Вычислить пределы, используя правило Лопиталя.
1. а) 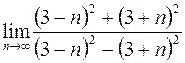 ; в)
; в) 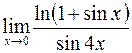 ;
;
б) 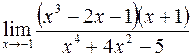 ; г)
; г) 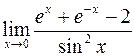 .
.
2. а) 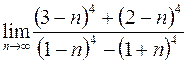 ; в)
; в) 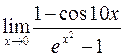 ;
;
б) 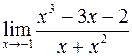 ; г)
; г)  .
.
3. а)  ; в)
; в) 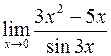 ;
;
б) 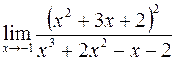 ; г)
; г) 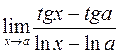 .
.
4. а)  ; в)
; в) 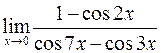 ;
;
б) 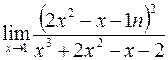 ; г)
; г) 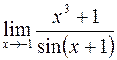 .
.
5. а) 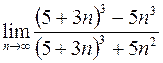 ; в)
; в) 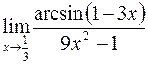 ;
;
б) 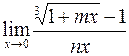 ; г)
; г) 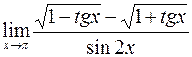 .
.
6. а) 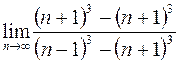 ; в)
; в) 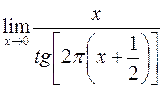 ;
;
б) 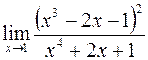 ; г)
; г)  .
.
7. а) 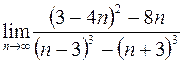 ; в)
; в) 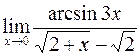 ;
;
б) 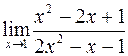 ; г)
; г) 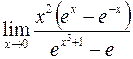 .
.
8. а) 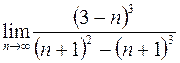 ; в)
; в) 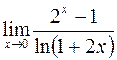 ;
;
б) 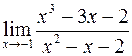 ; г)
; г) 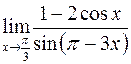 .
.
9. а) 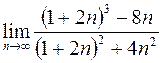 ; в)
; в) 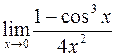 ;
;
б) 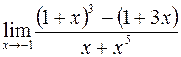 ; г)
; г) 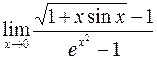 .
.
10. а)  ; в)
; в) 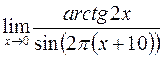 ;
;
б) 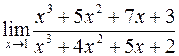 ; г)
; г) 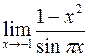 .
.
11. а) 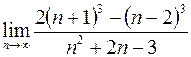 ; в)
; в)  ;
;
б) 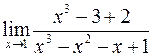 ; г)
; г) 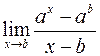 .
.
12. а) 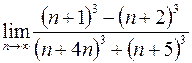 ; в)
; в)  ;
;
б) 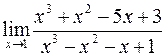 ; г)
; г) 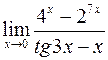 .
.
13. а)  ; в)
; в) 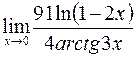 ;
;
б) 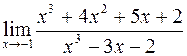 ; г)
; г)  .
.
14. а) 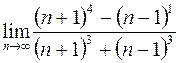 ; в)
; в) 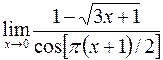 ;
;
б) 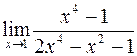 ; г)
; г) 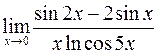 .
.
15. а) 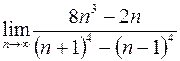 ; в)
; в) 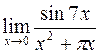 ;
;
б)  ; г)
; г) 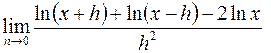 .
.
16. а) 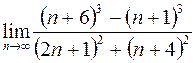 ; в)
; в) 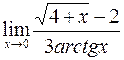 ;
;
б) 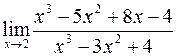 ; г)
; г) 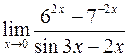 .
.
17. а) 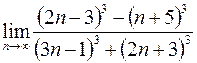 ; в)
; в)  ;
;
б) 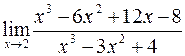 ; г)
; г) 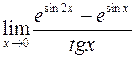 .
.
18. а)  ; в)
; в) 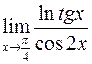 ;
;
б) 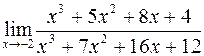 ; г)
; г) 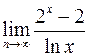 .
.
19. а) 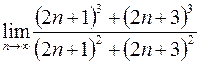 ; в)
; в)  ;
;
б) 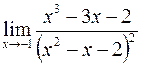 ; г)
; г) 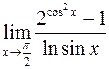 .
.
20. а) 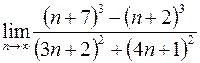 ; в)
; в)  ;
;
б) 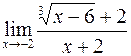 ; г)
; г) 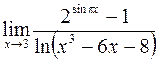 .
.
21. а) 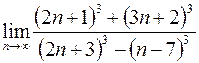 ; в)
; в) 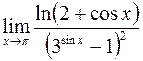 ;
;
б) 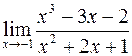 ; г)
; г) 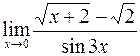 .
.
22. а)  ; в)
; в) 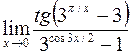 ;
;
б) 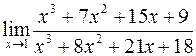 ; г)
; г)  .
.
23. а) 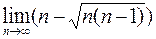 ; в)
; в) 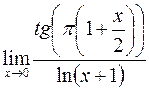 ;
;
б) 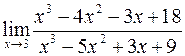 ; г)
; г)  .
.
24. а) 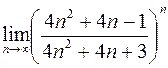 ; в)
; в) 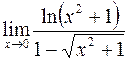 ;
;
б) 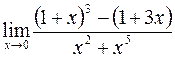 ; г)
; г)  .
.
25. а)  ; в)
; в)  ;
;
б) 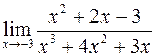 ; г)
; г)  .
.
26. а) 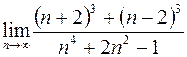 ; в)
; в) 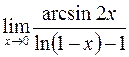 ;
;
б) 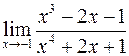 ; г)
; г) 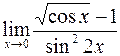 .
.
27. а) 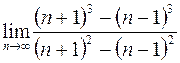 ; в)
; в) 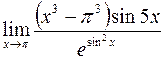 ;
;
б) 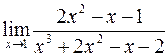 ; г)
; г) 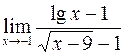 .
.
28. а)  ; в)
; в) 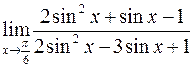 ;
;
б) 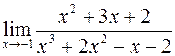 ; г)
; г)  .
.
29. а) 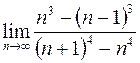 ; в)
; в) 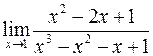 ;
;
б) 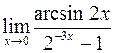 ; г)
; г) 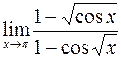 .
.
30. а) 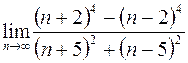 ; в)
; в) 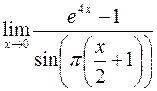 ;
;
б) 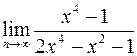 ; г)
; г) 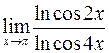 .
.
Date: 2015-09-02; view: 526; Нарушение авторских прав