
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Исследование функций. Угловой коэффициент касательной -уравнение касательной
|
|
ОДНОЙ ПЕРЕМЕННОЙ
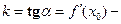 угловой коэффициент касательной
угловой коэффициент касательной 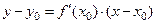 - уравнение касательной
- уравнение касательной
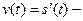 скорость,
скорость, 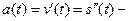 ускорение
ускорение
Формулы дифференцирования и таблица производных
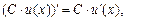 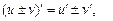 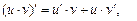 
| |||
1. 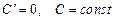
| 5. 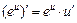
| 9. 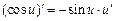
| 13. 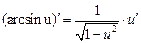
|
2. 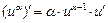 , , 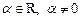
| 6. 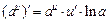
| 10. 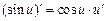
| 14. 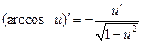
|
3. 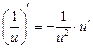
| 7. 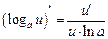
| 11. 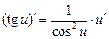
| 15. 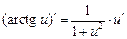
|
4. 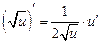
| 8. 
| 12. 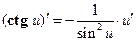
| 16. 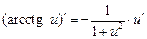
|
ИССЛЕДОВАНИЕ ФУНКЦИЙ
| Исследование на монотонность | Исследование на экстремум | Нахождение наибольшего и наименьшего значений функции на отрезке | ||
Функция возрастает (убывает) на промежутке, если на этом промежутке 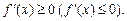
| Производная в точке экстремума 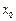 равна нулю или не существует и меняет знак: с + на равна нулю или не существует и меняет знак: с + на 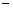 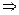 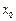 - точка максимума, с - точка максимума, с 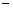 на + на + 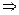 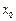 - точка минимума. - точка минимума.
| Они находятся среди значений функции в точках этого отрезка, в которых 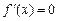 или не существует, и значений функции на концах отрезка. или не существует, и значений функции на концах отрезка.
| ||
| АСИМПТОТЫ ГРАФИКА ФУНКЦИИ | ||||
| Вертикальные | Наклонные | Горизонтальные | ||
Уравнение 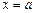 , если , если 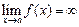 . .
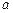 , как правило, является точкой разрыва 2 рода или граничной точкой области определения. , как правило, является точкой разрыва 2 рода или граничной точкой области определения.
| Уравнение 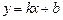 , где , где
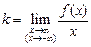 , , 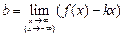 . .
| Уравнение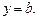 Это частный случай наклонной асимптоты, если угол наклона к оси
Это частный случай наклонной асимптоты, если угол наклона к оси 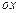 равен 0 равен 0 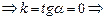 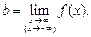
| ||
Примеры. 1. Найти асимптоты графика функции 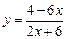 . 1) Ищем вертикальные асимптоты.
. 1) Ищем вертикальные асимптоты. 
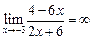
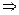
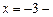 вертикальная асимптота. 2) Ищемнаклонные асимптоты.
вертикальная асимптота. 2) Ищемнаклонные асимптоты. 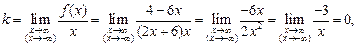
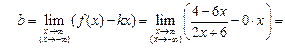
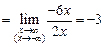 . Получили
. Получили 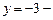 наклонная (горизонтальная) асимптота.
наклонная (горизонтальная) асимптота.
2. Найти наибольшее значение функции 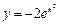 на отрезке
на отрезке 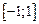 . 1)
. 1) 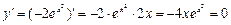 при
при 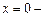 критическая точка, принадлежащая данному отрезку. 2) Вычисляем значения функции в критической точке и на концах отрезка и выбираем наибольшее из них:
критическая точка, принадлежащая данному отрезку. 2) Вычисляем значения функции в критической точке и на концах отрезка и выбираем наибольшее из них: 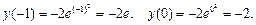
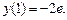
Получили, что наибольшее значение равно -2.
 ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ
Date: 2015-09-02; view: 552; Нарушение авторских прав