Свободное распространение плоской волны и нормировка интеграла Гюйгенса-Френеля

Интеграл можно использовать для количественного расчёта дифракционных картин. В качестве простой тестовой задачи целесообразно рассмотреть свободное распространение световой волны.

Р и с. 4.19

Введём обозначения, показанные на рис. 4.19. Окружим источник электромагнитных колебаний S воображаемой поверхностью x, которая представляет собой сферу радиуса a, совпадающую с волновым фронтом. Рассмотрим возмущение в точке P вне этой поверхности как результат совместного действия всех элементов ds этой поверхности. Согласно формуле суммарное возмущение в точке P определяется равенством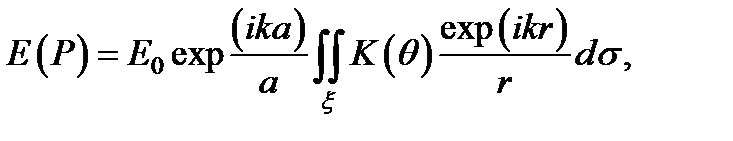

где учтено, что источник испускает сферическую волну, исходная амплитуда которой E ₀. Для того, чтобы вычислить интеграл, разбиваем поверхность x на зоны Френеля. Как известно, для этого вокруг точки P построим сферы с радиусами ,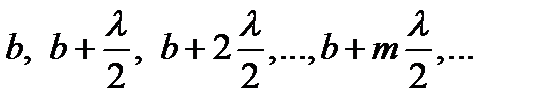

где b = OP, O – точка пересечения SP с волновым фронтом.

Пусть a и b велики по сравнению с длиной волны, тогда можно предположить, что в любой зоне величина K постоянна и в зоне m равна K_m. Из рисунка видно, что .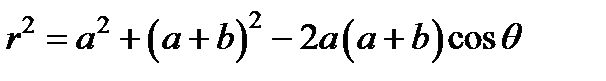

Следовательно, 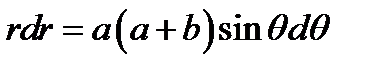и значит .

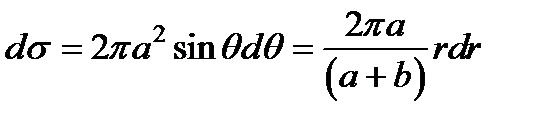Следовательно, вклад зоны m в E ₀(P) равен

.

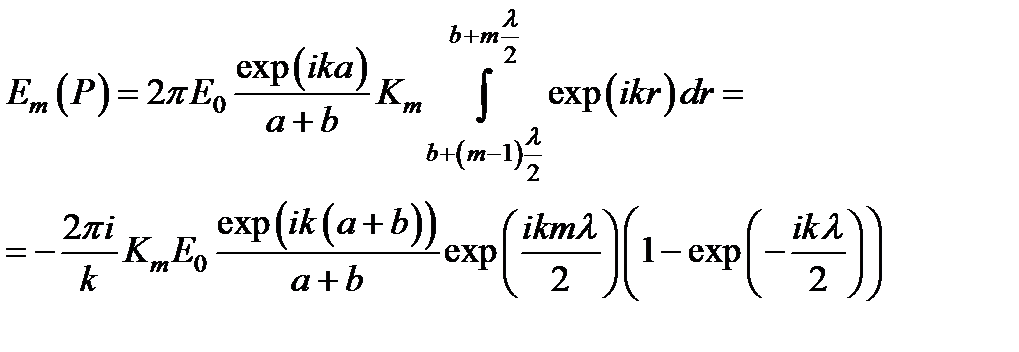Так как kl = 2 p, последние два множителя сводятся к

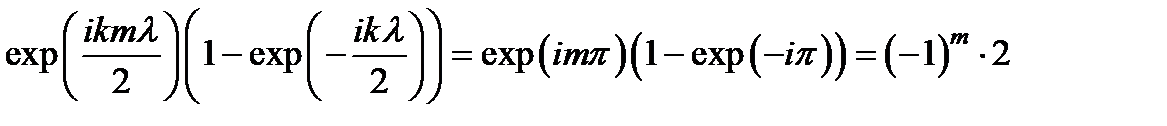
и, следовательно, .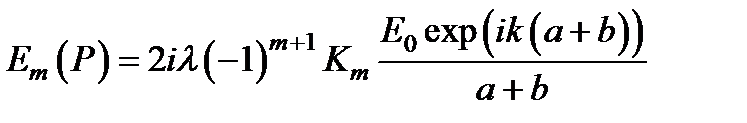

Заметим, что вклады следующих друг за другом зон имеют разные знаки. Результирующий эффект в точке P получается суммированием вкладов от всех зон, т.е.

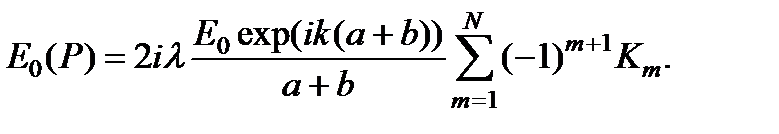
Ряд

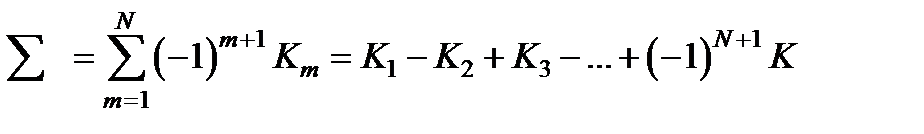
можно приближённо вычислить по методу Шустера. Сгруппируем члены этого ряда следующим образом:

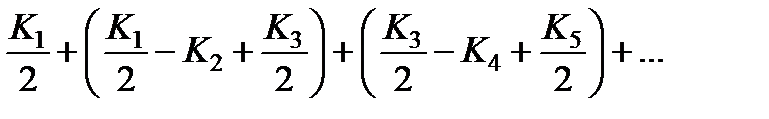
Поскольку величина каждого K_m лишь немного отличается от величины соседних K_{m – 1} и K_{m + 1}, то можно показать, что (в зависимости от чётности m) такая сумма равна K ₁/2 ± K_N /2.

Тогда формулу перепишем в виде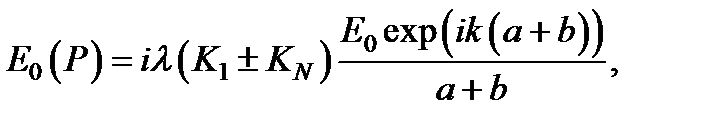

где верхний знак берётся при нечётном N, а нижний при чётном.

Воспользовавшись, амплитуду суммарного колебания в точке P представим так

.

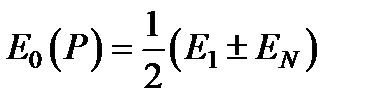Для последней зоны, видимой из P, MP становиться касательной к волновому фронту, то есть q = p /2, и, как говорилось выше, для такого q величина K, по предположению, равна нулю. Следовательно, K_N = 0 и сводится к выражению ,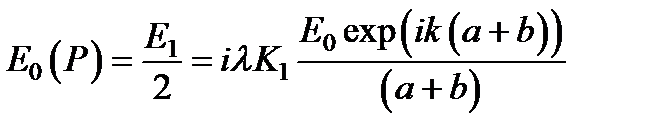

показывающему, что полное возмущение в P равняется половине возмущения, обусловленного действием только первой зоны.

Если отвлечься от проведённых построений, связанных с введением фиктивных вторичных источников на поверхности x, то можно утверждать, что точечный источник S, испускающий сферическую волну, должен создавать в точке P, удалённой от него на расстояние (a + b), колебания с амплитудой E ₀(P), определяемой равенством 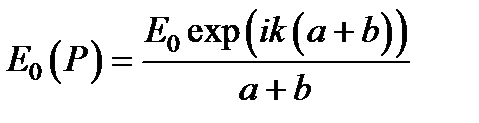. Сравнивая это выражение с, находим, что , или 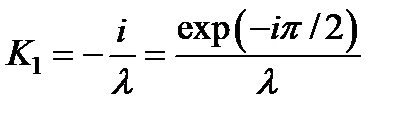. Множитель exp(- ip /2) можно объяснить, если предположить, что вторичные волны отстают по фазе на четверть периода от первичной волны.

Присутствие второго множителя становится понятным, если допустить, что амплитуды вторичных и первичных волн относятся как 1: l. При этих допущениях относительно амплитуды и фазы вторичных волн принцип Гюйгенса-Френеля правильно описывает распространение сферических волн в свободном пространстве. Однако дополнительные предположения нужно рассматривать просто как удобный способ интерпретации математических выражений.

Полученные выше результаты находятся в хорошем согласии с опытом и результатами метода “векторных диаграмм”.Полагая K (q) = K (0) = 1 / il, запишем интеграл в виде .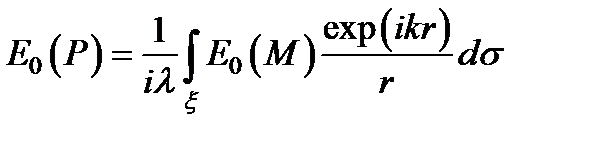

Замечания относительно метода Френеля. Замечания касаются как самой спирали Френеля в качестве рабочего инструмента, так и вида дифракционной картины в зависимости от радиуса отверстия.

1. При решении некоторых вопросов, если дело ограничивается первым витком спирали Френеля, т. е. первой зоной, и мы не претендуем на особую точность результатов, то вполне достаточно первый виток принимать за окружность. Погрешность будет при этом для многих случаев несущественной.

2. Метод зон Френеля позволяет сравнительно просто найти интенсивность света только в точке Р, лежащей на оси круглого отверстия в экране. Расчет же распределения интенсивности для всей дифракционной картины значительно сложнее. Вся картина обладает круговой симметрией и представляет собой чередующиеся светлые и темные кольца, плавно переходящие друг в друга.

Если в отверстии экрана укладывается 1-я зона Френеля или ее часть, то интенсивность максимальна в центре картины (т.е. в точке Р) и монотонно убывает при удалении от точки Р. Если отверстие в экране открывает две первые зоны Френеля, то в окрестности точки Р возникает темное круглое пятно, а вокруг него – светлое кольцо. С увеличением числа т открытых зон в отверстии экрана увеличивается и число светлых и темных колец. На рис 4.20 показано распределение интенсивности I от расстояния r до центра дифракционной картины при различном числе т открытых зон Френеля. Когда же в отверстии укладывается большое число зон Френеля, интенсивность вблизи точки Р оказывается почти равномерной и лишь у краев геометрической тени отверстия наблюдается чередование весьма узких светлых и темных кольцевых полос.

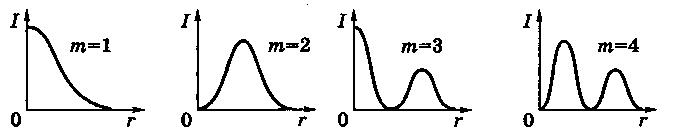Р и с. 4.20

3. При вычислении результатов интерференции элементарных волн приходится считать, что амплитуда колебаний от элементов dσ волновой поверхности зависит от угла J между нормалью к элементу dσ и направлением на точку Р, для которой ведется расчет. Амплитуда максимальна при J = 0 и монотонно убывает до нуля при стремлении J к p /2, т.е. нет «обратной» волны. Это обстоятельство остается не обоснованным в теории Френеля.

4. Расчет по методу Френеля дает неправильное значение фазы результирующего колебания. Для полностью открытой волновой поверхности она отличается на p /2 от действительной. Это видно из рис. 4.5, г. Направление спирали Френеля в ее начале дает в точке наблюдения фазу колебаний от центрального элемента первой зоны. Это и есть то значение фазы, которое соответствует действительности. Результирующий же вектор от полностью открытой волновой поверхности повернут на p /2 против часовой стрелки, т.е. отстает по фазе на p /2. Таким образом, постулат Френеля, правильно задавая амплитуды вспомогательных источников, неудачно определяет их фазы.

Для большинства задач вопрос о фазе не имеет значения, ибо нас интересует интенсивность результирующей волны, которая пропорциональна квадрату амплитуды. Значение же последней метод Френеля дает правильное.

Итак, несмотря на некоторые недостатки, метод Френеля в вопросах расчета интенсивности волн для многих случаев является весьма плодотворным.

Date: 2015-08-06; view: 1004; Нарушение авторских прав