
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Модуляция амплитуды
|
|
Колебание с модулированной амплитудой может быть представлено в виде 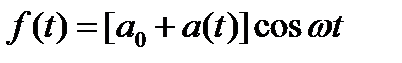 ,
,
где a (t) описывает модуляцию; w – частота гармонического колебания; 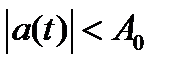 .
.
Прежде всего, рассмотрим случай, когда а (t) является гармонической функцией
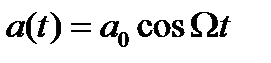
с частотой W<< w. Тогда равенство примет вид:
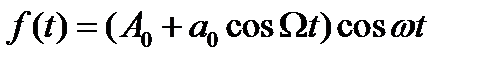 .
.
График этого колебания изображeн на рис. 2.14.
| A 0- a 0 |
| A 0+ a 0 |

Р и с. 2.14
С помощью формул для косинуса суммы и разности углов выражение преобразуют к виду

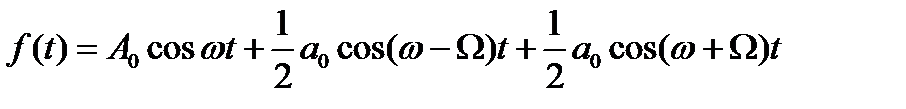 ,
,
| ω |
| ω |
| ω |
| ω |
Р и с. 2.15
из которого можно заключить, что спектральный состав колебания сводится к трeм частотам: w, w + W, w – W (рис. 2.17). Частота w называется несущей, а частоты w + W, w – W - боковыми.
Если а (t) является не гармонической, но периодической функцией с периодом T = 2 p /W, то её можно представить в виде ряда Фурье по частотам, кратным W. Подставив ряд Фурье в формулу и преобразовав каждый из членов ряда после умножения на cos wt аналогично тому, как это было сделано при переходе от к, получим ряд, в который входят частоты w, w + n W, w – n W (n = 1,2,3,…), т.е. спектр состоит из набора частот, отстоящих друг от друга на W в обе стороны от несущей частоты w (рис. 2.16).
| ω 0 |
| ω |
| ω |
| ω |


Р и с. 2.16 Р и с. 2.17
Ширина спектра определяется шириной спектра функции а (t). Если а (t) является непериодической функцией, которая представляется интегралом Фурье, то её спектр непрерывный. Подставляя в этом случае в выражение для а (t) в виде интеграла Фурье и преобразовывая гармонические составляющие аналогично предыдущим случаям, получим для модулированного колебания непрерывный спектр, простирающийся в обе стороны от несущей частоты w 0 (рис. 2.17). Таким образом, в этом случае ширина спектра определяется шириной спектра а (t).
Date: 2015-08-06; view: 478; Нарушение авторских прав